ЛЕКЦИЯ 6 ВЫЧИСЛЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ГАУССА

ЛЕКЦИЯ 6 ВЫЧИСЛЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ГАУССА • Рассмотренный нами метод Гаусса используют для вычисления обратной матрицы. • Прежде, чем научиться его применять на практике, дадим несколько определений.

• ОПРЕДЕЛЕНИЕ 1. Квадратная матрица размерности n, на главной диагонали которой стоят 1, • а остальные элементы 0, называется • единичной матрицей размерности n. • Назовем ее Е. • 1 0 0. . . 0 • 0 1 0. . . 0 • 0 0 1. . . 0 • . . • 0 0 0. . . 1

• ОПРЕДЕЛЕНИЕ 2. Для любого действительного числа, а 0, существует число, называемое обратным для «а» , такое, что • • а-1 а = а а -1 = 1. •

• Аналогичным свойством обладают и матрицы. • Пусть А - произвольная квадратная матрица размерности n. • Тогда справедлива следующая запись • Е А = А Е = А. •

• Матрица В называется обратной для матрицы А, • если А В = В А = Е, • где Е - единичная матрица.

• Матрица А имеет обратную матрицу тогда и только тогда, • когда ее определитель не равен нулю. • Вычислим обратную матрицу для заданной матрицы А • (

Контрольный пример • этот пример следует взять в качестве контрольного при нахождении обратной матрицы методом Гаусса в соответствующей лабораторной работе:

Контрольный пример • Дано: матрица А = • 1 2 -1 • 1 3 1 • 2 4 -1 • Обозначим искомую обратную матрицу Х. • Х= • х1 y 1 z 1 • x 2 y 2 z 2 • x 3 y 3 z 3

• Так как Х - обратная матрица для матрицы А, • то по определению обратной матрицы можно записать А Х = Е , • где Е - единичная матрица • Е= • 1 0 0 • 0 1 0 • 0 0 1

• Перемножим матрицы А и Х по правилу умножения матриц и • приравняем элементы матрицыпроизведения А Х • соответствующим элементам матрицы Е.

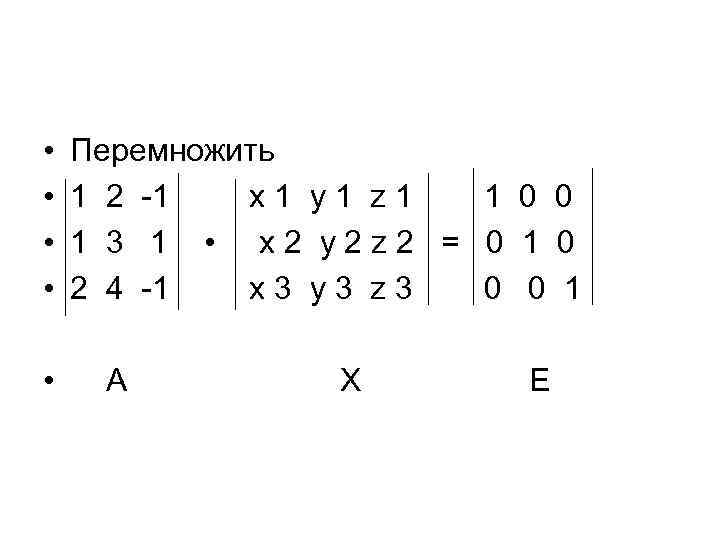
• • • Перемножить 1 2 -1 х1 y 1 z 1 1 0 0 1 3 1 • x 2 y 2 z 2 = 0 1 0 2 4 -1 x 3 y 3 z 3 0 0 1 А Х Е

Получение 1 столбца матрицыпроизведения • 1). 1 -ю строку умножаем на 1 -й столбец, • все складываем и получаем 1 -ый элемент 1 -го столбца произведения. • 2). 2 - строку умножаем на 1 - й столбец , • все складываем и • получаем 2 -ой элемент 1 -го столбца произведения. • 3). 3 строку умножаем на 1 столбец, • все складываем и • получаем 3 -ий элемент 1 -го столбца произведения.

Получим 1 -ю систему: • х 1+ 2 х 2 - х 3= 1 • х 1+ 3 х 2+ х 3= 0 • 2 х 1+ 4 х 2 - х 3= 0

2 -ой столбец матрицыпроизведения • • • 1). 1 -ю строку умножаем на 2 -ой столбец, все складываем, получаем 1 -ый элемент 2 -го столбца произведения. 2). 2 -ю строку умножаем на 2 -ой столбец, все складываем, получаем 2 -ой элемент 2—го столбца произведения. 3). 3 -ю строку умножаем на 2 -ой столбец, Все складываем, получаем 3 -ий элемент 2—го столбца произведения.

Получили 2 - ю систему линейных уравнений. • у 1+ 2 у 2 - у 3= 0 • у 1 + 3 у 2+ у 3 = 1 • 2 у 1 + 4 у 2 - у 3 = 0

3 -ий столбец матрицыпроизведения • • • 1). 1 -ю строку умножаем на 3 -ий столбец, все складываем, получаем 1 -ый элемент 3 -го столбца произведения. 2). 2 -ю строку умножаем на 3 -й столбец, все складываем, получаем 2 -ой элемент 3—го столбца произведения, все складываем, • 3). 3 -ю строку умножаем на 3 -й столбец, • все складываем, • получаем 3 -й элемент 3—го столбца произведения.

Получили 3 - ю систему линейных уравнений. • z 1+ 2 z 2 - z 3= 0 • z 1+3 z 2+z 3=0 • 2 z 1+4 z 2 -z 3=1

• Найти матрицу Х означает решить эти 3 системы линейных уравнений. • Каждую из них можно решить методом Гаусса. •

• Однако эти системы отличаются друг от друга только столбцом свободных членов. • Поэтому рационально решать их вместе. • Объединим все исходные данные в общую таблицу (как в методе Гаусса, при этом столбцов свободных членов будет 3).

• • Х 1 1 1 2 Х 2 2 3 4 Х 3 Св. член Св. Член -1 1 0 0 1 0 -1 0 0 1

• Применим метод Гаусса для решения систем линейных уравнений к этой таблице трижды • с разными столбцами свободных членов. Получим • х1 • х2 • х3 ( Это 1 -ый столбец обратной матрицы). • у1 • у2 • у3 ( Это 2 -ой столбец обратной матрицы). • z 1 • z 2 • z 3 ( Это 3 -й столбец обратной матрицы).

• В результате вычислений получим следующую обратную матрицу • Х= • - 7 -2 5 • 3 1 -2 • -2 0 1

• Этот результат должен быть получен в контрольном примере к лабораторной работе. • После нахождения обратной матрицы в программе следует сделать проверку, • а именно, перемножить исходную и обратную матрицы, • чтобы получилась единичная матрица.

Проверка • • 1 1 2 2 -1 -7 -2 5 3 1 -2 4 -1 -2 0 1 А Х 1 0 0 = 0 1 0 0 0 1 Е

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ • 1. Какая матрица называется единичной? • 2. Какая матрица называется обратной к данной матрице? • 2. Почему метод Гаусса для решения систем линейных уравнений можно использовать для нахождения обратной матрицы к данной?

• ВНИМАНИЕ! Для закрепления изученного теоретического материала следует выполнить лабораторную работу № 7.