Лекция 6 Вязкость Молекулярно-кинетические свойства растворов ВМС и

Лекция 6 Вязкость. Молекулярно-кинетические свойства растворов ВМС и золей. 1

Вязкость разбавленных золей и растворов ВМС Ньютоновские жидкости. 2

Теория вязкости разбавленных агрегативно устойчивых золей (Эйнштейн) Постулаты Эйнштейна: частицы жесткие; частицы не взаимодействуют между собой; отсутствует “проскальзывание” частиц в дисперсионной среде (объем вращения). η = ηо (1 + αφ), где φ ― объемная доля частиц, α ― коэффициент, зависящий от формы частиц: α = 2. 5 для сферических и α > 2. 5 для анизодиаметрических частиц, η и ηо ― вязкость золя и дисперсионной среды, соответственно. Относительная вязкость: Удельная вязкость: 3

Вязкость разбавленных растворов ВМС (Штаудингер) Постулаты Штаудингера: макромолекулы ― короткие жесткие палочки; макромолекулы не взаимодействуют между собой. где К — константа, М — молекулярная масса ВМС, с — концентрация. Приведенная вязкость: Характеристическая вязкость: (определение молекулярной массы полимеров) 4

Характеристическая вязкость: Обобщенное уравнение Штаудингера (определение формы макромолекул) [η] = КМα ; lg[η] = lg. K + αlg. M где α — зависимая от формы макромолекулы безразмерная величина: α = 0 — сферическая молекула, α = 0. 5 — идеальный статистический клубок ( глобулярный белок), α = 1 ÷ 1. 8 — длинная жесткая молекула, α = 2 — сильно заряженная молекула 5 полиэлектролита.

Вязкость концентрированных растворов ВМС Неньютоновские жидкости 1 — ньютоновская жидкость; 2 — растворы ВМС со сферическими(а) и вытянутыми (б) макромолекулами; 3 — структурированная система Структурная вязкость — следствие образования надмолекулярных структур (сетки, каркасы). Для структурированных растворов η = ηн + ηстр где ηн — нормальная вязкость ламинарного потока и ηстр — структурная вязкость. Аномалии вязкости (аномальная вязкость) — отклонения от законов Ньютона и Пуазейля. 6

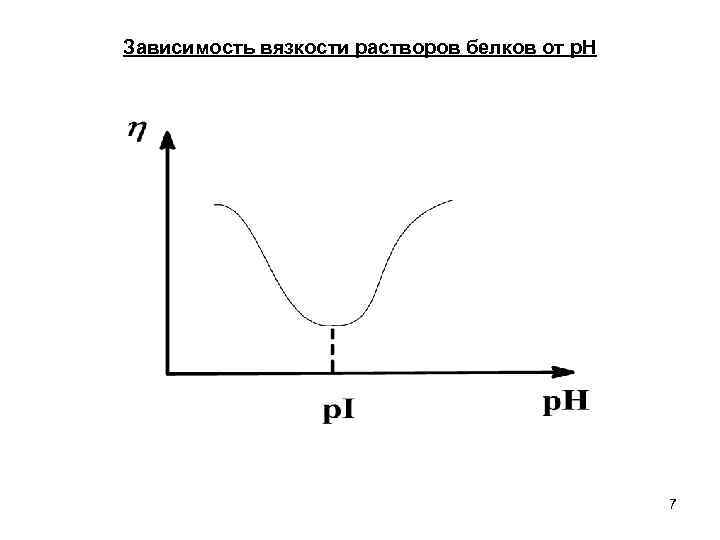Зависимость вязкости растворов белков от р. Н 7

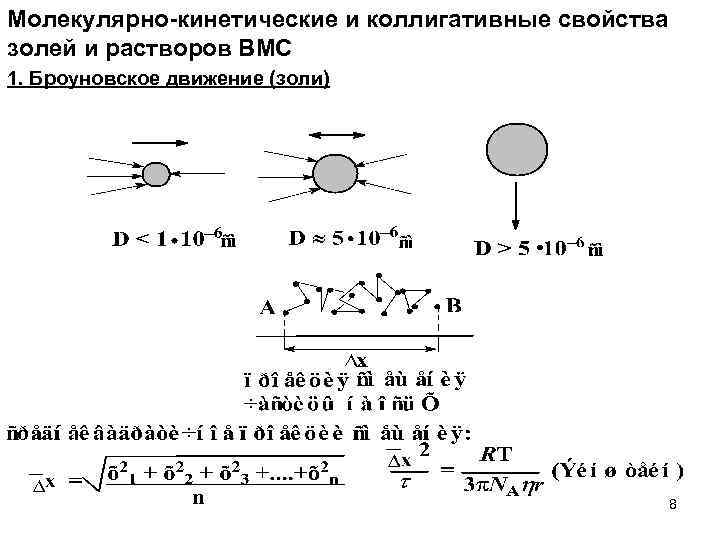Молекулярно-кинетические и коллигативные свойства золей и растворов ВМС 1. Броуновское движение (золи) 8

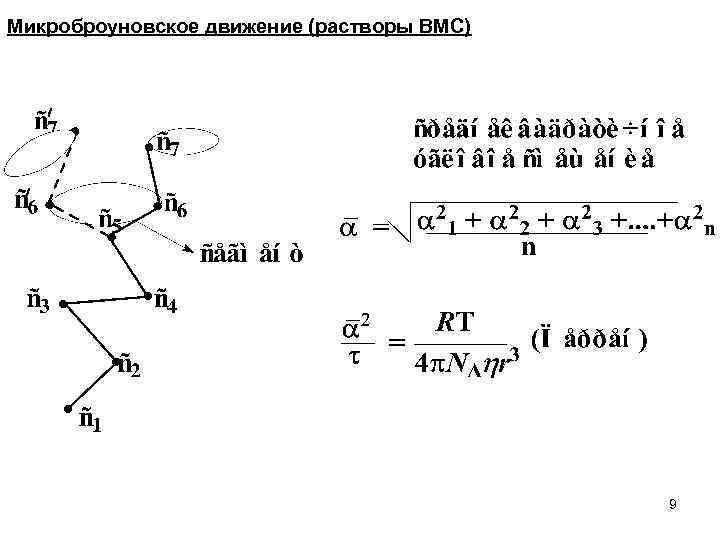Микроброуновское движение (растворы ВМС) 9

2. Диффузия 10

Особенности броуновского движения и диффузии в золях и растворах ВМС — процессы замедлены вследствие больших масс и размеров частиц и макромолекул по сравнению с размерами ионов электролитов и молекул неэлектролитов; — в растворах ВМС эти процессы носят сегментный характер для длинных гибких макромолекул, а для анизодиметрических макромолекул, кроме того, приобретают и вращательный характер. Физиологическое значение диффузии — возникновение потенциала действия клетки; — насыщение крови кислородом в легких; — основа процессов обмена веществ. Взаимосвязь броуновского движения и диффузии 11

3. Осмотическое давление В истинных растворах = i с. RT (Вант-Гофф). В коллоидных дисперсных системах где W — количество вещества дисперсной фазы, m — масса частицы, V — объем системы, NA — число Авогадро, n — частичная концентрация. Особенности осмотического давления в золях и растворах ВМС — осмотическое давление золей очень мало ( красного золя золота = 0. 00045 атм. ); — осмотическое давление золей непостоянно ( способность частиц к агрегации и распад агрегатов на исходные частицы); — осмотическое давление растворов ВМС выше, чем должно быть по закону Вант-Гоффа; — при увеличении концентрации макромолекул осмотическое давление растет не пропорционально увеличению концентрации, а в 12 большей степени;

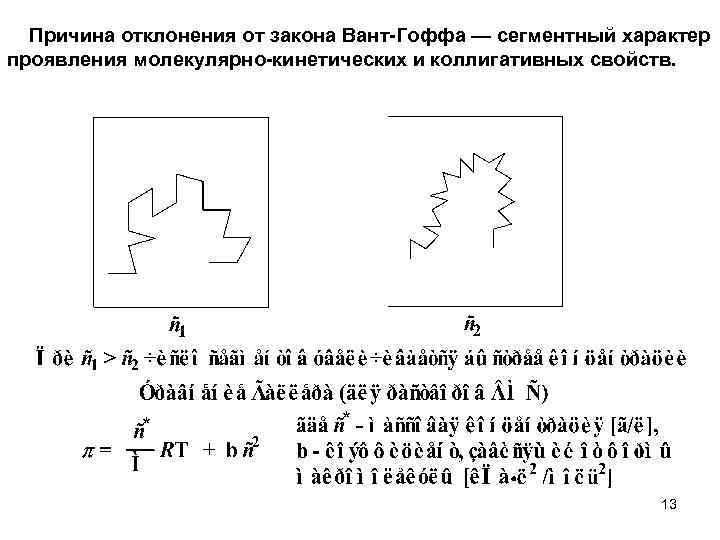Причина отклонения от закона Вант-Гоффа — сегментный характер проявления молекулярно-кинетических и коллигативных свойств. 13

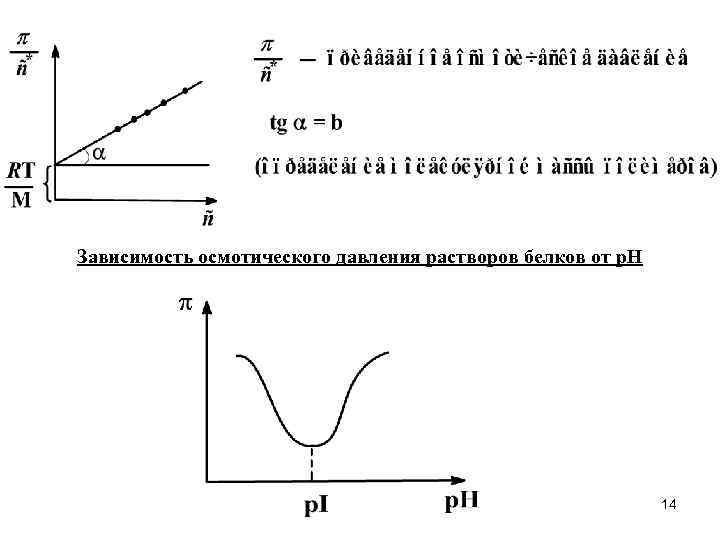Зависимость осмотического давления растворов белков от р. Н 14

Онкотическое давление (крови) = (нмс) + (вмс) + Q + (фэ) 7. 7 — 8. 1 атм. (нмс) — осмотическое давление низкомолекулярных соединений и электролитов; (вмс) — осмотическое давление белков; Q — давление набухания белков; (фэ) — осмотическое давление суспензий форменных элементов; (вмс) + Q = (онк) 0, 04 атм. Физиологическое значение онкотического давления — распределение минеральных веществ между кровью и тканями (особенно в капиллярах); — образование первичной мочи в канальцах почек. 15

4. Мембранное равновесии Доннана количество ионов Cl–, проникающих в клетку = х; количество ионов Na+, проникающих в клетку = х. Движущая сила — диффузия До перераспределения: [Na+]снаружи = [Cl–]снаружи = сн [Na+]внутри = св После перераспределения [Na+]снаружи = [Cl–]снаружи = сн – х [Na+]внутри = св + х [Cl–]внутри = х Условие термодинамического равновесия [Na+]внутри ∙ [Cl–]внутри = [Na+]снаружи ∙ [Cl– ]снаружи (св + х) ∙ х = (сн – х) ∙ (сн – х) 16

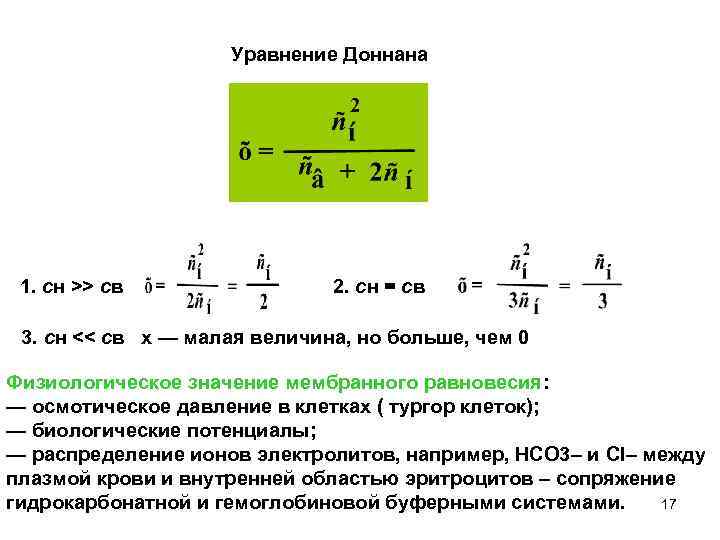Уравнение Доннана 1. сн >> св 2. сн = св 3. сн << св х — малая величина, но больше, чем 0 Физиологическое значение мембранного равновесия: — осмотическое давление в клетках ( тургор клеток); — биологические потенциалы; — распределение ионов электролитов, например, НСО 3– и Cl– между плазмой крови и внутренней областью эритроцитов – сопряжение 17 гидрокарбонатной и гемоглобиновой буферными системами.