Лекция 6 u Геометрические приложения определённого интеграла

Лекция 6 u Геометрические приложения определённого интеграла

Площадь плоской фигуры o 1. o Площадь плоской фигуры, граница которой задана в прямоугольных декартовых координатах: Если непрерывная кривая (кусочно-непрерывная) задана в прямоугольных декартовых координатах уравнением , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикальными линиями и осью Ох: определяется формулой: Пример 1: Вычислить площадь плоской фигуры, ограниченной параболой, прямыми х=1, х=3 и осью Ох: . Искомая площадь равна:

Примеры (декартовая С. К. ) o Пример 2: Вычислить площадь плоской фигуры, ограниченной кривой: и осью ординат. Здесь изменены роли функции и аргумента. Эффективнее рассматривать зависимость Тогда Рассмотрим случай произвольной непрерывной (кусочно-непрерывной) на отрезке. Пусть фигура ограничена теперь сверху и снизу функциями:

Геометрический смысл o В случае, если ограничивающие фигуру линии находятся в верхней части системы координат, то сдвигаем графики функций вверх на величину С: вверх и тогда получим:

Правильная область по определённому напрвлению o Площадь фигуры, изображённой на предыдущем рисунке может быть найдена по формуле: (*) Замечание: формула (*) вычисления площади плоской фигуры верна для правильных в направлении оси Oy областей. Область D называется правильной в направлении оси Oy, если выполнено: т. е. отрезок, соединяющих любые две точки области также ей принадлежит.

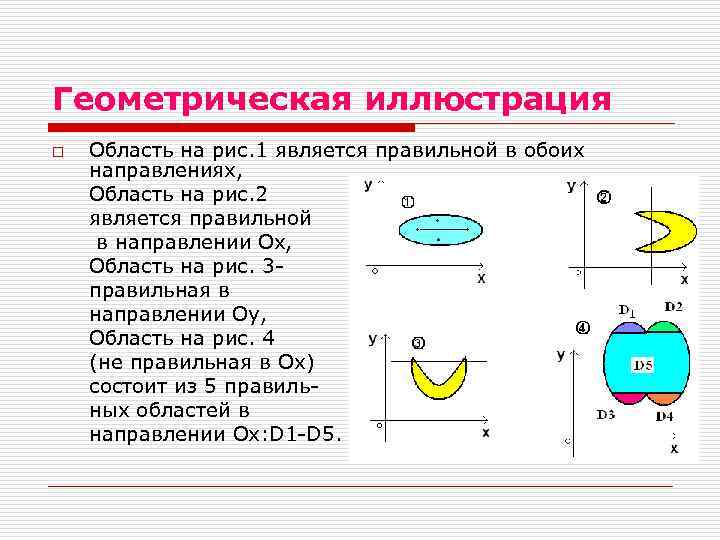Геометрическая иллюстрация o Область на рис. 1 является правильной в обоих направлениях, Область на рис. 2 является правильной в направлении Ox, Область на рис. 3 правильная в направлении Оy, Область на рис. 4 (не правильная в Ох) состоит из 5 правильных областей в направлении Ox: D 1 -D 5.

Площадь фигуры, ограниченной линиями, заданных в параметрической форме o Пусть границы области заданы уравнениями: Площадь криволинейной трапеции, ограниченной этой линией, прямыми , осью Ox, есть: Пример 3: Вычислить площадь фигуры, ограниченной эллипсом:

Пример 3 o Ввиду симметрии фигуры, достаточно вычислить площадь четвёртой части её: заметим, что: Тогда:

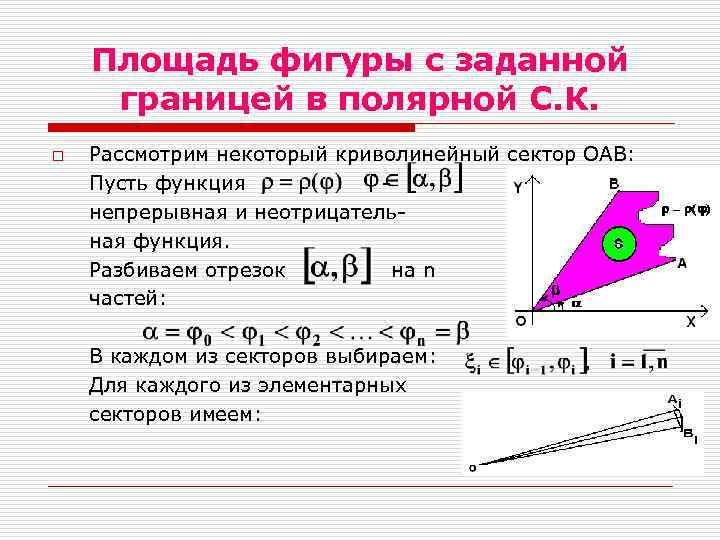Площадь фигуры с заданной границей в полярной С. К. o Рассмотрим некоторый криволинейный сектор ОАВ: Пусть функция непрерывная и неотрицательная функция. Разбиваем отрезок на n частей: В каждом из секторов выбираем: Для каждого из элементарных секторов имеем:

Вывод формулы площади в ПСК o Тогда имеем: тогда получим интегральную сумму, предел которой равен: Пример 4: Найти площадь фигуры, заключённой внутри лемнискаты Бернулли: В силу симметрии фигуры, имеем:

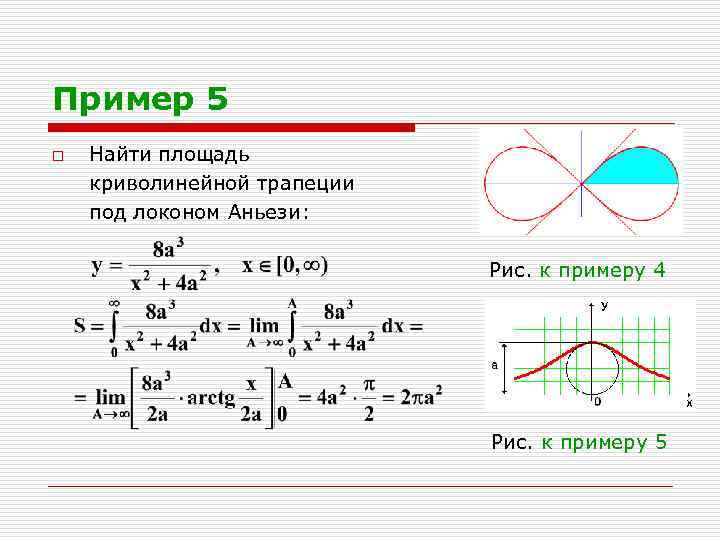Пример 5 o Найти площадь криволинейной трапеции под локоном Аньези: Рис. к примеру 4 Рис. к примеру 5

Длина дуги плоской линии o o Пусть плоская линия L задана уравнением в ДСК: где , т. е. гладкая линия без изломов. Рассмотрим разбиение отрезка на n частей (произвольной длины): Проведём хорды, соединяя последовательно точки разбиения отрезка, длины которых равны, соответственно: Т. о. получим ломаную линию, вписанную в дугу, для которой имеем: Длиной дуги называется предел, к которому стремится длина вписанной ломаной линии при стремлении частичных отрезков длин к нулю и

Длина дуги плоской линии o Указанное выше определение в аналитическом виде: (*) Теорема 1: Если функция непрерывна со своей производной на отрезке задания, то такой предел (*)существует и длина дуги линии, заданной зависимостью выражается формулой: доказательство: Обозначим:

Доказательство Т 1 o Рассмотрим: , где -согласно теореме Лагранжа. Тогда имеем: и переходя к пределу, получим: (т. к. - непрерывная функция, то ) и тогда:

Пример 1: o Рассмотрим окружность с центром в начале координат. Тогда верхняя часть её (полуокружность) описывается функцией: - непрерывная функция Поэтому, формулу для вычисления длины дуги законно применить только на отрезке: на котором функция непрерывна вместе с производной :

Длина дуги линии, заданной уравнением в параметрической форме Далее получим: т. е. длина полуокружности равна. Пусть функция задана уравнением в параметрической форме: , где - -гладкие функции и тогда имеем:

Пример 2 o Найти длину одной арки циклоиды: Для этого найдём производные: Тогда длина дуги вычисляется по формуле:

Длина дуги линии, заданной уравнением в полярной СК o Пусть линия задана уравнением: Тогда, после преобразований: получим:

Пример 3 o Найти длину линии, заданной уравнением: Т. к. то т. о. И

Объём тела вращения o Пусть Г – есть кривая, описываемая в ДСК x. Oy непрерывной положительной функцией Для вычисления элементарного объёма тела вращения линии Г вокруг оси Ох произведём разбиение отрезка на n частей: и тогда элементарный объём тела, ограниченного плоскостями вычисляется по формуле:

Формула для вычисления объёма тела вращения o После чего, переходим к пределу и получаем формулу для определения объёма тела вращения вокруг оси Ох: т. е. Если вращение кривой происходит вокруг другой оси координат, например Oy, тогда объём вычисляется по формуле:

Пример 4 (ТР № 15) o Вычислить объём тела вращения фигуры, заданной уравнением: вокруг оси Оy. Тогда имеем:

Площадь поверхности тела вращения o Пусть функция вместе со своей производной элементарная площадь поверхности тела вращения вокруг оси Ох равна: - непрерывная. Тогда: Если вращение производится вокруг оси Oy, то соответствующая площадь определяется по формуле:

Пример 5: Вычислить площадь поверхности тора: вращение вокруг оси Ох. Находим: и o