Лекция 6 u Функция от случайных величин u

Лекция 6 u Функция от случайных величин u Числовые характеристики случайных величин

Функция от случайной величины o Рассмотрим на вероятностном пространстве случайную величину. Возьмем обычную числовую функцию , . Поставим в соответствие каждому элементарному событию число по формуле. Тогда получим новую случайную величину , которая называется функцией от случайной величины. Функция от дискретной случайной величины - также дискретная случайная величина, так как она не может принимать больше значений, чем. Пусть случайная величина распределена по закону … …

Функция от дискретной случайной величины o Тогда случайная величина будет иметь следующую таблицу распределения: При этом, если существуют столбцы, у которых , то эти столбцы объединяются, а соответствующие вероятности складываются. … …

Пример 1 o Пусть задан ряд распределения -1 1 1/4 o 0 1/2 1/4 Тогда для случайной величины распределения будет иметь вид 0 1 1/2 1/4+1/4=1/2 ряд

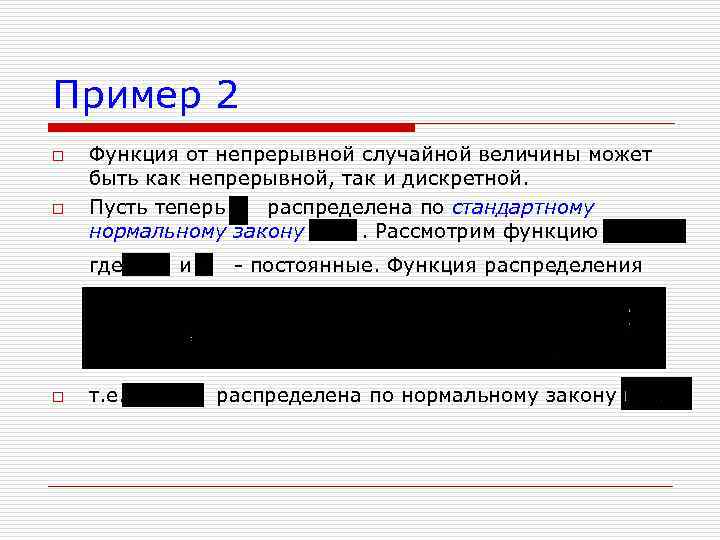Пример 2 o o Функция от непрерывной случайной величины может быть как непрерывной, так и дискретной. Пусть теперь распределена по стандартному нормальному закону. Рассмотрим функцию где o т. е. и - постоянные. Функция распределена по нормальному закону

Числовые характеристики случайных величин o Моментом порядка дискретной случайной величины , принимающей значения с вероятностью , называется число при условии, что ряд сходится абсолютно, т. е. o o o Моментом порядка непрерывной случайной величины с плотностью вероятности называется число при условии, что интеграл сходится абсолютно, то есть. Момент первого порядка называется математическим ожиданием (средним значением) случайной величины

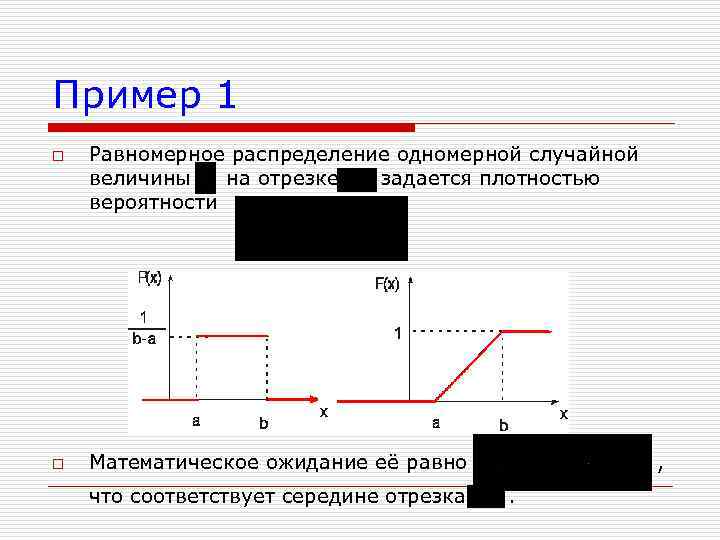Пример 1 o o Равномерное распределение одномерной случайной величины на отрезке задается плотностью вероятности Математическое ожидание её равно что соответствует середине отрезка , .

Пример 2 o Распределение Пуассона: с вероятностью

Пример 3 o Нормальное распределение:

Пример 4 Некто стоит перед дверью своей квартиры и пытается открыть её, перебирая ключи из связки; при этом испробованный ключ: а) не исключается при дальнейших попытках; б) устраняется из дальнейших попыток. Сколько в среднем придется сделать попыток, чтобы открыть дверь? а) Пусть - число попыток, понадобившихся для открывания двери, . Событие состоит в том, что ключ от двери попадется при -той попытке, а все предыдущие попытка были безуспешными; o

Решение примера 4 o если испробованный ключ возвращается в связку, то вероятность

Решение примера 4 o б) если испробованный ключ устраняется из связки, то и

МО функции от случайной величины o o Рассмотрим теперь математическое ожидание функции от случайной величины. Теорема. Пусть - дискретная случайная величина (непрерывная случайная величина), принимающая значения соответственно с вероятностью (имеющая плотность вероятности ), а - новая случайная величина, где - некоторая функция. Тогда математическое ожидание равно , , если ряд (интеграл) сходится абсолютно.

Дисперсия случайной величины o o Математическое ожидание называется -м центральным моментом, если существует. Центральный момент 2 -го порядка называется дисперсией случайной величины и обозначается. (*) Дисперсия является удобной характеристикой разброса значений около её среднего значения – математического ожидания. Согласно. Отсюда, справедлива следующая формула для дисперсии:

Дисперсия для дискретных и непрерывных распределений случайной величины Величина называется среднеквадратичным отклонением случайной величины от её МО. Из рассмотренной выше теоремы и из (*)следует: если - дискретная случайная величина, то ; если -непрерывная случайная величина, то

Свойства математического ожидания 1. Математическое ожидание суммы случайных величин равно сумме математических ожиданий при условии, что 2. 3. и конечны , где любые постоянные. Это следует из свойства 1. Если случайные величины и независимы, то при условии, что 4. Если , то . и конечны

Свойства дисперсии 1. 2. 3. Дисперсия постоянной величины равна нулю: , так как. Верно и обратное утверждение: если , то с вероятностью 1 случайная величина принимает значение, равное константе: =const. дисперсия суммы конечного числа попарно независимых случайных величин равна сумме дисперсий слагаемых: Если , то постоянная, т. к. , где - любая

Пример: o o Пусть случайная величина распределена по биномиальному закону. Найдем и. Введем случайные величины , равные числу успехов при том испытании в серии из испытаний Бернулли. Если вероятность успеха при каждом испытании равна , то. Поэтому Число успехов в серии из испытаний равно сумме. Отсюда ввиду независимости свойств МО и дисперсии имеем и

Закон больших чисел o Стандартное теоретико–вероятностное заключение – – не позволяет предсказать, произойдет событие А или нет. Исключение составляют лишь те случаи, когда либо очень мало, либо очень близко к единице. При этом можно утверждать, что событие А практически невозможно или соответственно практически достоверно. Так, например, если подбрасывать монету 1000 раз, то событие, состоящее в выпадении герба все 1000 раз, можно считать практически невозможным, а событие, состоящее в том, что герб выпадет хотя бы один раз, практически достоверным

Закон больших чисел o o o Рассмотрим ряд результатов, известных под названием «закон больших чисел» и позволяющих делать подобные предсказания. Всякое утверждение о малости некоторой величины естественно формулировать в терминах предельного перехода. С этой целью введём новый тип сходимости случайных величин: сходимость по вероятности. Последовательность случайных величин сходится по вероятности к случайной величине , если Обозначение , . Этот тип сходимости означает, что, каково бы ни было , найдется число , такое, что для всех вероятность неравенства будет сколь угодно малой (т. е это событие будет практически невозможным).

Теорема Чебышева o Пусть – последовательность попарно независимых случайных величин, дисперсии которых ограничены в совокупности: , . Тогда последовательность случайных величин сходится по вероятности к нулю при , т. е. , - любое Следствие: Пусть в условиях теоремы Чебышева случайные величины имеют одинаковые математические ожидания: . Тогда последовательность при сходится по вероятности к математическому ожиданию : .

Правило среднего арифметического o o повторив раз измерение величины и получив в качестве результатов случайные величины за приближенное значение принимают среднее арифметическое из наблюдённых значений Если при измерениях отсутствует систематическая ошибка, т. е. , то согласно закону больших чисел при достаточно больших с вероятностью, сколь угодно близкой к 1, будет получен результат , произвольно мало отличающийся от истинного значения.

Теорема Бернулли o Пусть - число успехов в серии из испытаний Бернулли и - вероятность успеха при каждом испытании. Тогда последовательность частот при сходится по вероятности к. Эта теорема утверждает, что для фиксированного достаточно большого частота будет отклоняться от вероятности менее чем на. Это не значит, что разность будет малой для всех достаточно больших. Теорема гарантирует лишь, что эти большие отклонения будут появляться очень редко.

Пример o o Технический контролёр проверяет партию однотипных приборов. С вероятностью 0, 01 прибор может иметь дефект А и независимо от этого с вероятностью 0, 02 – дефект В. В каких границах будет заключено практически наверняка число бракованных изделий в партии из 1000 приборов, если за вероятность практической достоверности принимается 0, 997? Пусть - число бракованных изделий в партии из приборов , - вероятность дефекта одного прибора

Пример (продолжение) Тогда o , . Из неравенства Чебышева Отсюда . , , . Тогда

Центральная предельная теорема Теорема (ЦПТ): Пусть - последовательность независимых и одинаково распределенных случайных величин, для которых , , , . Тогда для последовательности справедливо равенство: где - функция Лапласа.

Суть ЦПТ o o Если на некоторую случайную величину (с. в. )влияет большое количество других независимых случайных величин, то её распределение будет близко к нормальному. В природе так и бывает: на большинство случайных процессов и объектов оказывает влияние большое количество разнообразных случайных факторов, и поэтому параметры этих процессов оказываются случайными и имеющими почти нормальное распределение. Хотя это бывает не всегда. Поэтому возникает необходимость проверки, можно ли считать ту или иную с. в. нормально распределённой или нет? Вся классическая теория мат. статистики строится только для нормально распределённых с. в.

Пример задачи (ЦПТ): o o o В кассе учреждения имеется сумма 3500 тысяч рублей, в очереди стоит 20 человек, сумма , которую нужно выплатить отдельному человеку, является случайной величиной со средним значением 150 т. р. и. Найти: Вероятность того, что суммы не хватит для выплаты всем людям из очереди; Какую сумму нужно иметь в кассе, чтобы с вероятностью её хватило всем из очереди. Решение: При уже можно считать, что с. в. достаточно близка к нормальной, с параметрами:

Продолжение примера Тогда: 1. 2. По таблицам находим, что для этого должно быть:

Независимость случайных величин o o o Случайные величины называются независимыми, если закон распределения каждой из них не меняется от того, какие значения принимает вторая случайная величина. (Курс доллара и счёт матча в футболе). Выявление действительного наличия зависимости между с. в. используют понятия коэффициента ковариации, коэффициента корреляции: Коэффициентом ковариации между с. в. Называют число: Из свойств МО легко устанавливается, что для независимых с. в. ковариация Отсюда следует, что чем сильнее зависимость между с. в. , тем больше величина коэффициента ковариации.

Коэффициент корреляции o o Важным недостатком этого показателя является то, что величина коэффициента ковариации зависит от абсолютных значений с. в. Этого недостатка лишён следующий показатель: Коэффициентом корреляции между с. в. Называют число Коэффициент корреляции является нормированным показателем, т. е. он не зависит от абсолютных значений с. в. Если с. в. Являются независимыми, то он также равен нулю. При наличии линейной зависимости между с. в. . Т. о. коэффициент корреляции принимает значения от -1 до +1.