 Лекция 6 Теорема Гаусса - Маркова 1
Лекция 6 Теорема Гаусса - Маркова 1
 УСЛОВИЯ Теоремы Гаусса - Маркова 0) Если модель Yi = β 1 + β 2 Xi + ui , i = 1, …, n правильно специфицирована (Модель линейна по параметрам, спецификация корректна) 1) Xi детерминированы и не все равны между собой (nonstochastic) Требование детерминированности может быть так же ослаблено до предопределенности- т. е. регрессором может выступать случайная величина, но к моменту наблюдения ее значение уже определено 2
УСЛОВИЯ Теоремы Гаусса - Маркова 0) Если модель Yi = β 1 + β 2 Xi + ui , i = 1, …, n правильно специфицирована (Модель линейна по параметрам, спецификация корректна) 1) Xi детерминированы и не все равны между собой (nonstochastic) Требование детерминированности может быть так же ослаблено до предопределенности- т. е. регрессором может выступать случайная величина, но к моменту наблюдения ее значение уже определено 2
 УСЛОВИЯ Теоремы Гаусса - Маркова 2) E(ui) = 0 во всех наблюдениях, Несмещенность в среднем «наблюдаемых» значений зависимой переменной относительно «теоретических» На самом деле это требование несущественно, если в модель включена константа, т. к. смещение случайной составляющей просто может учитываться константой 3) D(ui) = σu 2, D (e i )=D (e j ) (гомоскедастичность) Дисперсия ошибки ui одинакова для всех наблюдений i Для всех наблюдений степень влияния возмущающего фактора одинаково. 3
УСЛОВИЯ Теоремы Гаусса - Маркова 2) E(ui) = 0 во всех наблюдениях, Несмещенность в среднем «наблюдаемых» значений зависимой переменной относительно «теоретических» На самом деле это требование несущественно, если в модель включена константа, т. к. смещение случайной составляющей просто может учитываться константой 3) D(ui) = σu 2, D (e i )=D (e j ) (гомоскедастичность) Дисперсия ошибки ui одинакова для всех наблюдений i Для всех наблюдений степень влияния возмущающего фактора одинаково. 3
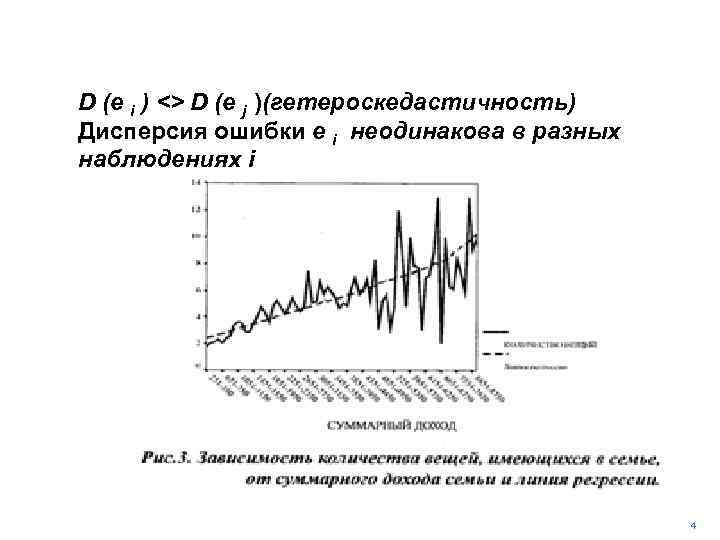 D (e i ) <> D (e j )(гетероскедастичность) Дисперсия ошибки e i неодинакова в разных наблюдениях i 4
D (e i ) <> D (e j )(гетероскедастичность) Дисперсия ошибки e i неодинакова в разных наблюдениях i 4
 4) cov(ui, uj) = 0 при i ≠ j (отсутствие автокорреляции- ошибки в разных наблюдениях не связаны между собой) 5
4) cov(ui, uj) = 0 при i ≠ j (отсутствие автокорреляции- ошибки в разных наблюдениях не связаны между собой) 5
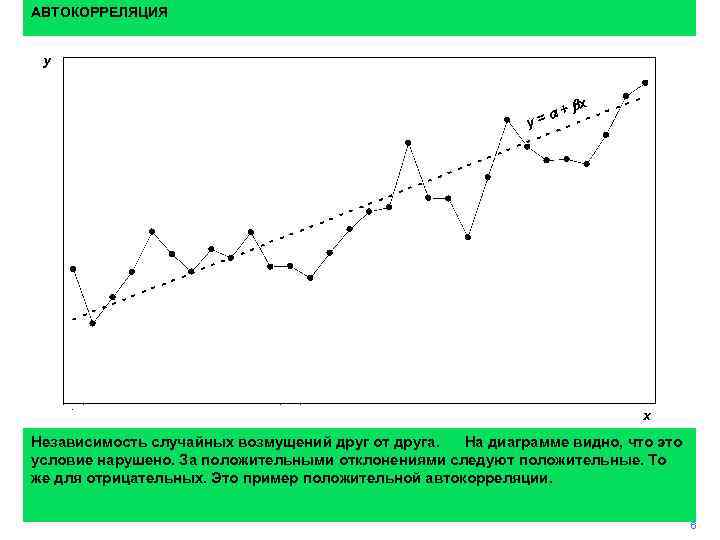 АВТОКОРРЕЛЯЦИЯ y y + =a bx x Независимость случайных возмущений друг от друга. На диаграмме видно, что это условие нарушено. За положительными отклонениями следуют положительные. То же для отрицательных. Это пример положительной автокорреляции. 6 6
АВТОКОРРЕЛЯЦИЯ y y + =a bx x Независимость случайных возмущений друг от друга. На диаграмме видно, что это условие нарушено. За положительными отклонениями следуют положительные. То же для отрицательных. Это пример положительной автокорреляции. 6 6
 5) Нормальность ошибок: Ошибки u имеют совместное многомерное нормальное распределение 7
5) Нормальность ошибок: Ошибки u имеют совместное многомерное нормальное распределение 7
 Предпосылки использования МНК (условия Гаусса – Маркова) 0. Регрессионная модель является линейной относительно параметров и корректно специфицирована. 1. Случайное отклонение имеет нулевое математическое ожидание (условное). 2. Дисперсия случайного члена постоянна. 3. Ошибки в разных наблюдениях независимы (некоррелированы) друг относительно друга. 4. Ошибки независимы (некоррелированы) с регрессорами. 5. Ошибки из себя представляют слабый белый (гауссовский) шум. 8
Предпосылки использования МНК (условия Гаусса – Маркова) 0. Регрессионная модель является линейной относительно параметров и корректно специфицирована. 1. Случайное отклонение имеет нулевое математическое ожидание (условное). 2. Дисперсия случайного члена постоянна. 3. Ошибки в разных наблюдениях независимы (некоррелированы) друг относительно друга. 4. Ошибки независимы (некоррелированы) с регрессорами. 5. Ошибки из себя представляют слабый белый (гауссовский) шум. 8
 Теорема Гаусса - Маркова При выполнении условий оценки МНК b 1 и b 2 являются BLUE (best linear unbiased estimator). Estimator – оценка, Unbiased – несмещенная, Linear – по Y, Best – это оценки с наименьшей дисперсией 9
Теорема Гаусса - Маркова При выполнении условий оценки МНК b 1 и b 2 являются BLUE (best linear unbiased estimator). Estimator – оценка, Unbiased – несмещенная, Linear – по Y, Best – это оценки с наименьшей дисперсией 9
 ОЦЕНКА –ESTIMATION Процесс получения численного значения параметра (оценивание) СВОЙСТВА ОЦЕНОК ПАРАМЕТРОВ • ЛИНЕЙНОСТЬ • НОРМАЛЬНОСТЬ • НЕСМЕЩЕННОСТЬ • СОСТОЯТЕЛЬНОСТЬ • ЭФФЕКТИВНОСТЬ 10
ОЦЕНКА –ESTIMATION Процесс получения численного значения параметра (оценивание) СВОЙСТВА ОЦЕНОК ПАРАМЕТРОВ • ЛИНЕЙНОСТЬ • НОРМАЛЬНОСТЬ • НЕСМЕЩЕННОСТЬ • СОСТОЯТЕЛЬНОСТЬ • ЭФФЕКТИВНОСТЬ 10
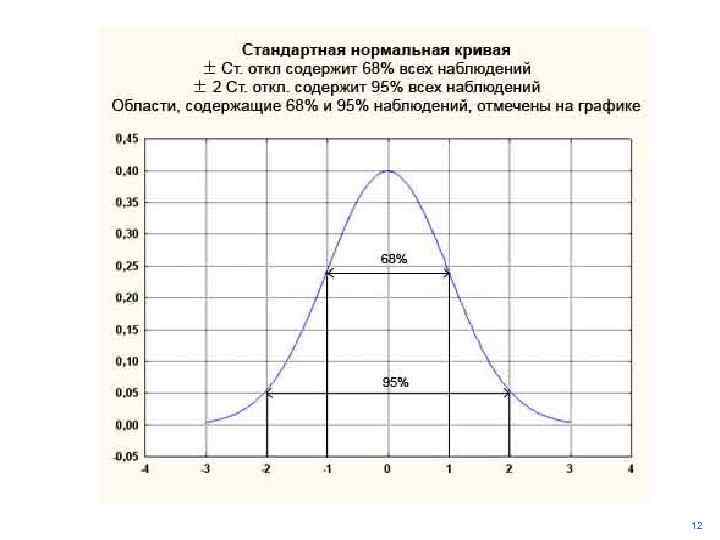
 СВОЙСТВА ОЦЕНОК ПАРАМЕТРОВ • НОРМАЛЬНОСТЬ ОПРЕДЕЛЕНИЕ Оценка является нормальной, если ее распределение –нормально АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ ОПРЕДЕЛЕНИЕ Оценка является нормальной, если ее распределение -нормально В ПРЕДЕЛЕ (число наблюдений стремится к бесконечности) 11
СВОЙСТВА ОЦЕНОК ПАРАМЕТРОВ • НОРМАЛЬНОСТЬ ОПРЕДЕЛЕНИЕ Оценка является нормальной, если ее распределение –нормально АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ ОПРЕДЕЛЕНИЕ Оценка является нормальной, если ее распределение -нормально В ПРЕДЕЛЕ (число наблюдений стремится к бесконечности) 11
 12
12
 СВОЙСТВА ОЦЕНОК ПАРАМЕТРОВ • НЕСМЕЩЕННОСТЬ ОПРЕДЕЛЕНИЕ Оценка является несмещенной, если ее математическое ожидание равно истинному значению параметра АСИМПТОТИЧЕСКАЯ НЕСМЕЩЕННОСТЬ ОПРЕДЕЛЕНИЕ Оценка является несмещенной, если ее математическое ожидание равно истинному значению параметра В ПРЕДЕЛЕ (число наблюдений стремится к бесконечности) 13
СВОЙСТВА ОЦЕНОК ПАРАМЕТРОВ • НЕСМЕЩЕННОСТЬ ОПРЕДЕЛЕНИЕ Оценка является несмещенной, если ее математическое ожидание равно истинному значению параметра АСИМПТОТИЧЕСКАЯ НЕСМЕЩЕННОСТЬ ОПРЕДЕЛЕНИЕ Оценка является несмещенной, если ее математическое ожидание равно истинному значению параметра В ПРЕДЕЛЕ (число наблюдений стремится к бесконечности) 13
 СВОЙСТВА ОЦЕНОК ПАРАМЕТРОВ • СОСТОЯТЕЛЬНОСТЬ ОПРЕДЕЛЕНИЕ Оценка является состоятельной, если она сходится по вероятности к истинному значению параметра • ЭФФЕКТИВНОСТЬ Эффективность является мерой отклонения от истинного значения для несмещенной оценки это эквивалентно вариации 14
СВОЙСТВА ОЦЕНОК ПАРАМЕТРОВ • СОСТОЯТЕЛЬНОСТЬ ОПРЕДЕЛЕНИЕ Оценка является состоятельной, если она сходится по вероятности к истинному значению параметра • ЭФФЕКТИВНОСТЬ Эффективность является мерой отклонения от истинного значения для несмещенной оценки это эквивалентно вариации 14
 Доказательство несмещенности оценки b 2 Для модели парной регрессии: Y = b 1 + b 2 X + u Оценка коэффициента наклона может быть представлена 15
Доказательство несмещенности оценки b 2 Для модели парной регрессии: Y = b 1 + b 2 X + u Оценка коэффициента наклона может быть представлена 15
 Доказательство несмещенности оценки b 2 Несмещенность оценки b 2 означает равенство ее математического ожидания истинному значению параметра, т. е β 2. 16
Доказательство несмещенности оценки b 2 Несмещенность оценки b 2 означает равенство ее математического ожидания истинному значению параметра, т. е β 2. 16
 Доказательство несмещенности оценки b 2 Таким образом, оценка b 2 коэффициента b 2 является несмещенной. 17
Доказательство несмещенности оценки b 2 Таким образом, оценка b 2 коэффициента b 2 является несмещенной. 17
 Доказательство несмещенности оценки b 1 Y = b 1 + b 2 X + u Приведена оценка МНК коэффициента β 1. 18
Доказательство несмещенности оценки b 1 Y = b 1 + b 2 X + u Приведена оценка МНК коэффициента β 1. 18
 Доказательство несмещенности оценки b 1 Y = b 1 + b 2 X + u Запишем последнюю формулу в более удобном для исследования виде. 19
Доказательство несмещенности оценки b 1 Y = b 1 + b 2 X + u Запишем последнюю формулу в более удобном для исследования виде. 19
 Доказательство несмещенности оценки b 1 Y = b 1 + b 2 X + u Непосредственной проверкой убеждаемся в несмещенности оценки b 1, т. е. равенству математического ожидания этой оценки истинному значению параметра b 1. 20
Доказательство несмещенности оценки b 1 Y = b 1 + b 2 X + u Непосредственной проверкой убеждаемся в несмещенности оценки b 1, т. е. равенству математического ожидания этой оценки истинному значению параметра b 1. 20
 Дисперсии оценок коэффициентов 21
Дисперсии оценок коэффициентов 21
 Оценка значимости коэффициента регрессии В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: и. Стандартная ошибка коэффициента регрессии определяется по формуле: где (1) - остаточная дисперсия на одну степень свободы. 22
Оценка значимости коэффициента регрессии В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: и. Стандартная ошибка коэффициента регрессии определяется по формуле: где (1) - остаточная дисперсия на одну степень свободы. 22
 Вычислим дисперсии параметров уравнения регрессии и дисперсию прогнозирования эндогенной переменной 1. Дисперсия параметра b 1 (6. 10) 23
Вычислим дисперсии параметров уравнения регрессии и дисперсию прогнозирования эндогенной переменной 1. Дисперсия параметра b 1 (6. 10) 23
 Величина стандартной ошибки совместно с t – распределением Стьюдента при (n – 2) степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала. Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t -критерия Стьюдента: , которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n - 2). 24
Величина стандартной ошибки совместно с t – распределением Стьюдента при (n – 2) степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала. Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t -критерия Стьюдента: , которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n - 2). 24
 Оценка значимости коэффициента bo Стандартная ошибка параметра определяется по формуле: (2) Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется t -критерий: его величина сравнивается с табличным значением при (n – 2) степенях свободы. 25
Оценка значимости коэффициента bo Стандартная ошибка параметра определяется по формуле: (2) Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется t -критерий: его величина сравнивается с табличным значением при (n – 2) степенях свободы. 25
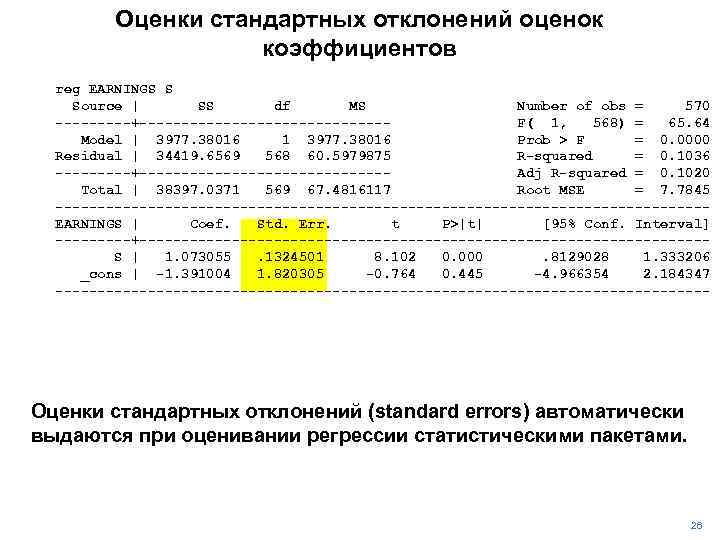 Оценки стандартных отклонений оценок коэффициентов reg EARNINGS S Source | SS df MS Number of obs = 570 -----+---------------F( 1, 568) = 65. 64 Model | 3977. 38016 1 3977. 38016 Prob > F = 0. 0000 Residual | 34419. 6569 568 60. 5979875 R-squared = 0. 1036 -----+---------------Adj R-squared = 0. 1020 Total | 38397. 0371 569 67. 4816117 Root MSE = 7. 7845 ---------------------------------------EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------S | 1. 073055. 1324501 8. 102 0. 000. 8129028 1. 333206 _cons | -1. 391004 1. 820305 -0. 764 0. 445 -4. 966354 2. 184347 --------------------------------------- Оценки стандартных отклонений (standard errors) автоматически выдаются при оценивании регрессии статистическими пакетами. 26
Оценки стандартных отклонений оценок коэффициентов reg EARNINGS S Source | SS df MS Number of obs = 570 -----+---------------F( 1, 568) = 65. 64 Model | 3977. 38016 1 3977. 38016 Prob > F = 0. 0000 Residual | 34419. 6569 568 60. 5979875 R-squared = 0. 1036 -----+---------------Adj R-squared = 0. 1020 Total | 38397. 0371 569 67. 4816117 Root MSE = 7. 7845 ---------------------------------------EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------S | 1. 073055. 1324501 8. 102 0. 000. 8129028 1. 333206 _cons | -1. 391004 1. 820305 -0. 764 0. 445 -4. 966354 2. 184347 --------------------------------------- Оценки стандартных отклонений (standard errors) автоматически выдаются при оценивании регрессии статистическими пакетами. 26
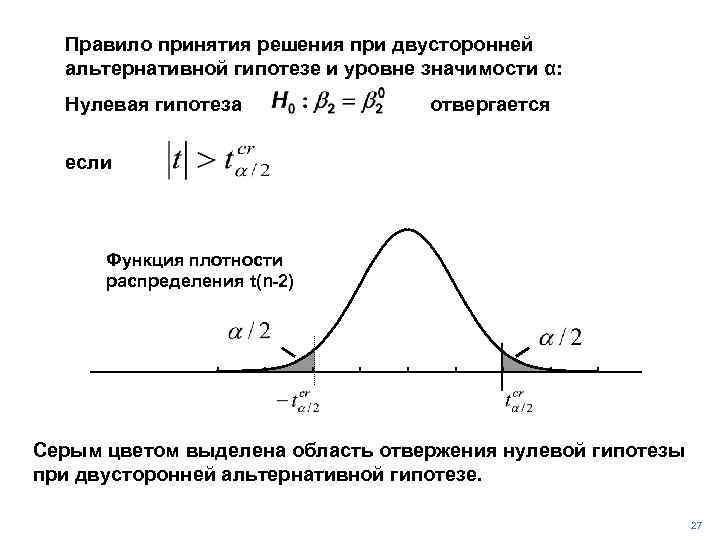 Правило принятия решения при двусторонней альтернативной гипотезе и уровне значимости α: Нулевая гипотеза отвергается если Функция плотности распределения t(n-2) Серым цветом выделена область отвержения нулевой гипотезы при двусторонней альтернативной гипотезе. 27
Правило принятия решения при двусторонней альтернативной гипотезе и уровне значимости α: Нулевая гипотеза отвергается если Функция плотности распределения t(n-2) Серым цветом выделена область отвержения нулевой гипотезы при двусторонней альтернативной гипотезе. 27
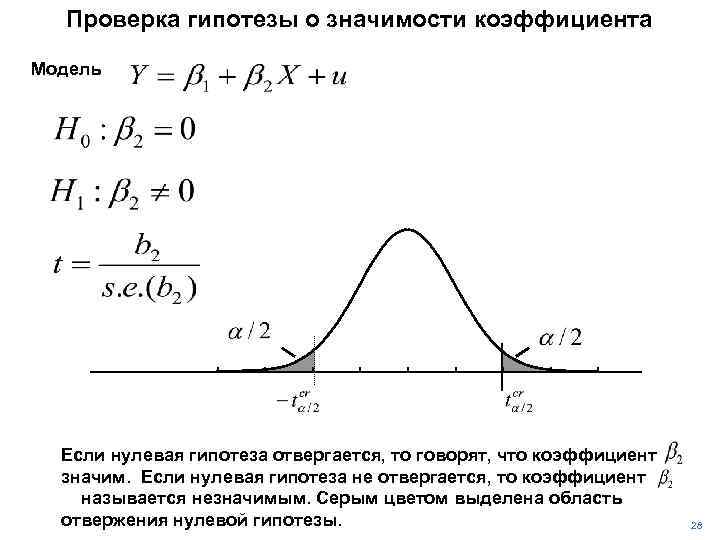 Проверка гипотезы о значимости коэффициента Модель Если нулевая гипотеза отвергается, то говорят, что коэффициент значим. Если нулевая гипотеза не отвергается, то коэффициент называется незначимым. Серым цветом выделена область отвержения нулевой гипотезы. 28
Проверка гипотезы о значимости коэффициента Модель Если нулевая гипотеза отвергается, то говорят, что коэффициент значим. Если нулевая гипотеза не отвергается, то коэффициент называется незначимым. Серым цветом выделена область отвержения нулевой гипотезы. 28
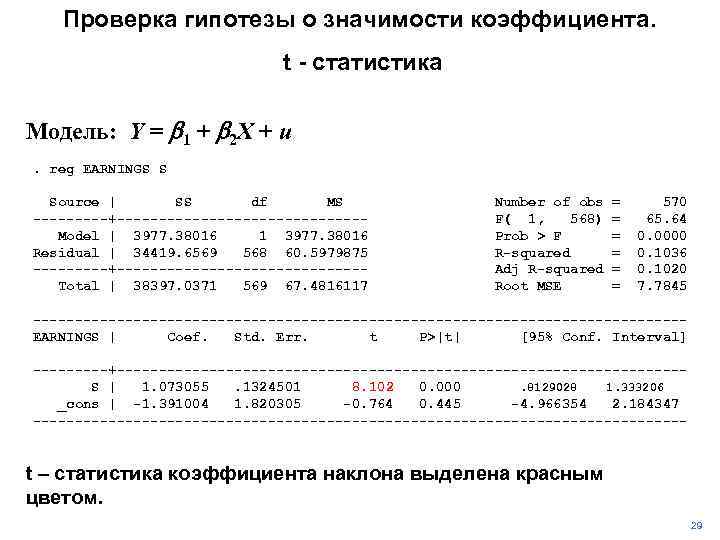 Проверка гипотезы о значимости коэффициента. t - статистика Модель: Y = b 1 + b 2 X + u. reg EARNINGS S Source | SS df MS -----+---------------Model | 3977. 38016 1 3977. 38016 Residual | 34419. 6569 568 60. 5979875 -----+---------------Total | 38397. 0371 569 67. 4816117 Number of obs F( 1, 568) Prob > F R-squared Adj R-squared Root MSE = = = 570 65. 64 0. 0000 0. 1036 0. 1020 7. 7845 ---------------------------------------EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------S | 1. 073055. 1324501 8. 102 0. 000. 8129028 1. 333206 _cons | -1. 391004 1. 820305 -0. 764 0. 445 -4. 966354 2. 184347 --------------------------------------- t – статистика коэффициента наклона выделена красным цветом. 29
Проверка гипотезы о значимости коэффициента. t - статистика Модель: Y = b 1 + b 2 X + u. reg EARNINGS S Source | SS df MS -----+---------------Model | 3977. 38016 1 3977. 38016 Residual | 34419. 6569 568 60. 5979875 -----+---------------Total | 38397. 0371 569 67. 4816117 Number of obs F( 1, 568) Prob > F R-squared Adj R-squared Root MSE = = = 570 65. 64 0. 0000 0. 1036 0. 1020 7. 7845 ---------------------------------------EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------S | 1. 073055. 1324501 8. 102 0. 000. 8129028 1. 333206 _cons | -1. 391004 1. 820305 -0. 764 0. 445 -4. 966354 2. 184347 --------------------------------------- t – статистика коэффициента наклона выделена красным цветом. 29
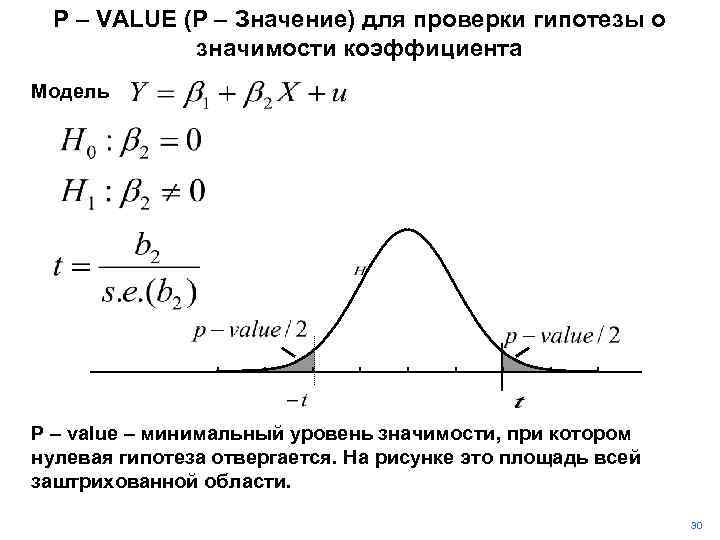 P – VALUE (P – Значение) для проверки гипотезы о значимости коэффициента Модель P – value – минимальный уровень значимости, при котором нулевая гипотеза отвергается. На рисунке это площадь всей заштрихованной области. 30
P – VALUE (P – Значение) для проверки гипотезы о значимости коэффициента Модель P – value – минимальный уровень значимости, при котором нулевая гипотеза отвергается. На рисунке это площадь всей заштрихованной области. 30
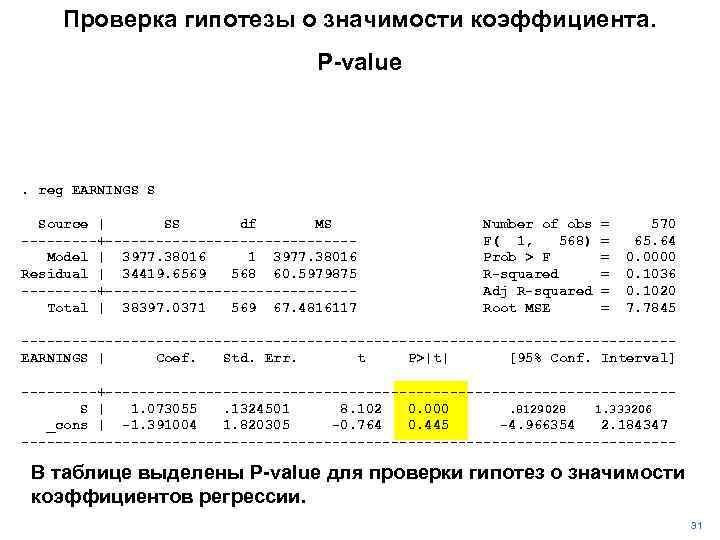 Проверка гипотезы о значимости коэффициента. P-value . reg EARNINGS S Source | SS df MS -----+---------------Model | 3977. 38016 1 3977. 38016 Residual | 34419. 6569 568 60. 5979875 -----+---------------Total | 38397. 0371 569 67. 4816117 Number of obs F( 1, 568) Prob > F R-squared Adj R-squared Root MSE = = = 570 65. 64 0. 0000 0. 1036 0. 1020 7. 7845 ---------------------------------------EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------S | 1. 073055. 1324501 8. 102 0. 000. 8129028 1. 333206 _cons | -1. 391004 1. 820305 -0. 764 0. 445 -4. 966354 2. 184347 --------------------------------------- В таблице выделены P-value для проверки гипотез о значимости коэффициентов регрессии. 31
Проверка гипотезы о значимости коэффициента. P-value . reg EARNINGS S Source | SS df MS -----+---------------Model | 3977. 38016 1 3977. 38016 Residual | 34419. 6569 568 60. 5979875 -----+---------------Total | 38397. 0371 569 67. 4816117 Number of obs F( 1, 568) Prob > F R-squared Adj R-squared Root MSE = = = 570 65. 64 0. 0000 0. 1036 0. 1020 7. 7845 ---------------------------------------EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------S | 1. 073055. 1324501 8. 102 0. 000. 8129028 1. 333206 _cons | -1. 391004 1. 820305 -0. 764 0. 445 -4. 966354 2. 184347 --------------------------------------- В таблице выделены P-value для проверки гипотез о значимости коэффициентов регрессии. 31
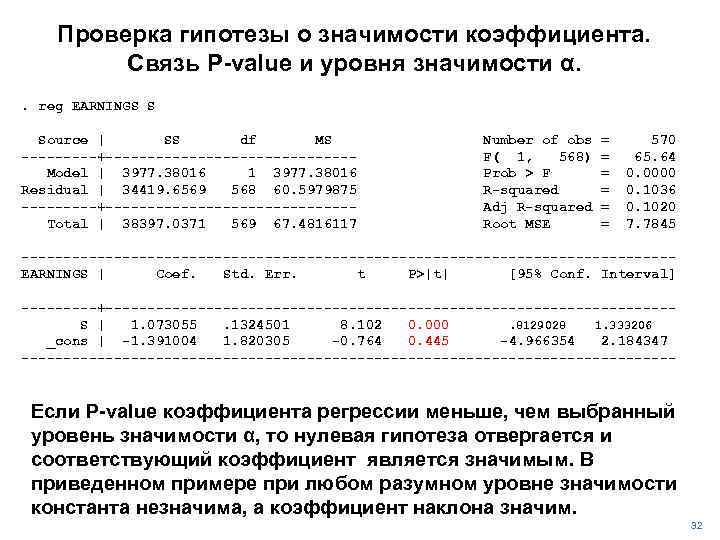 Проверка гипотезы о значимости коэффициента. Связь P-value и уровня значимости α. . reg EARNINGS S Source | SS df MS -----+---------------Model | 3977. 38016 1 3977. 38016 Residual | 34419. 6569 568 60. 5979875 -----+---------------Total | 38397. 0371 569 67. 4816117 Number of obs F( 1, 568) Prob > F R-squared Adj R-squared Root MSE = = = 570 65. 64 0. 0000 0. 1036 0. 1020 7. 7845 ---------------------------------------EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------S | 1. 073055. 1324501 8. 102 0. 000. 8129028 1. 333206 _cons | -1. 391004 1. 820305 -0. 764 0. 445 -4. 966354 2. 184347 --------------------------------------- Если P-value коэффициента регрессии меньше, чем выбранный уровень значимости α, то нулевая гипотеза отвергается и соответствующий коэффициент является значимым. В приведенном примере при любом разумном уровне значимости константа незначима, а коэффициент наклона значим. 32
Проверка гипотезы о значимости коэффициента. Связь P-value и уровня значимости α. . reg EARNINGS S Source | SS df MS -----+---------------Model | 3977. 38016 1 3977. 38016 Residual | 34419. 6569 568 60. 5979875 -----+---------------Total | 38397. 0371 569 67. 4816117 Number of obs F( 1, 568) Prob > F R-squared Adj R-squared Root MSE = = = 570 65. 64 0. 0000 0. 1036 0. 1020 7. 7845 ---------------------------------------EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------S | 1. 073055. 1324501 8. 102 0. 000. 8129028 1. 333206 _cons | -1. 391004 1. 820305 -0. 764 0. 445 -4. 966354 2. 184347 --------------------------------------- Если P-value коэффициента регрессии меньше, чем выбранный уровень значимости α, то нулевая гипотеза отвергается и соответствующий коэффициент является значимым. В приведенном примере при любом разумном уровне значимости константа незначима, а коэффициент наклона значим. 32


