Лекція 6 Тема Пряма на площині Різновиди рівняння

Лекція 6 Тема. Пряма на площині Різновиди рівняння прямої на площині Означення 1. Рівняння називається рівнянням деякої лінії на площині, якщо це рівняння задовольняє координати будьякої точки, що лежить на цій лінії, і не задовольняє координати жодної точки, що не лежить на цій лінії.

Пряма на площині може бути задана різними способами: точкою і вектором, паралельним даній прямій; двома точками; точкою і вектором, перпендикулярним до даної прямої, і т. д. Різним способам задання прямої відповідають різні види її рівнянь.

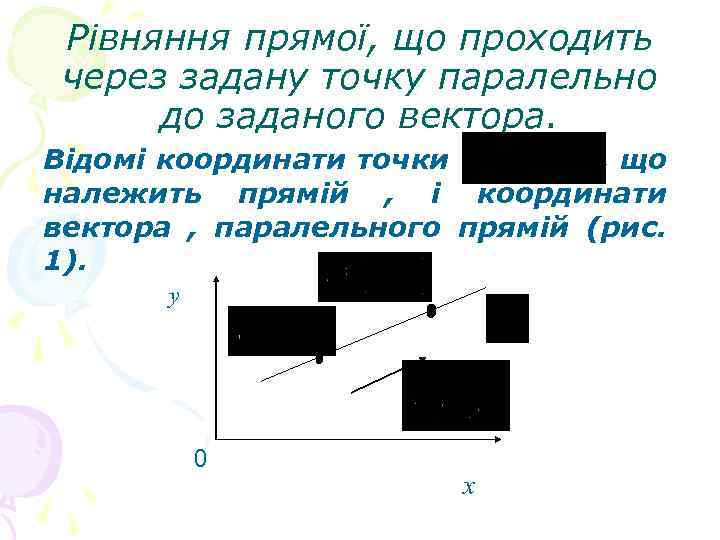Рівняння прямої, що проходить через задану точку паралельно до заданого вектора. Відомі координати точки , що належить прямій , і координати вектора , паралельного прямій (рис. 1). y 0 x

Потрібно вивести рівняння прямої як сукупності точок, координати яких задовольняють це рівняння. Означення 2. Будь-який вектор паралельний до прямої або який лежить на цій прямій, називається напрямним вектором прямої. Візьмемо змінну точку мій , тоді вектори є колінеарними. на пряі

З умови колінеарності цих векторів випливає пропорційність відповідних координат, тобто - каноніч- не рівняння прямої на площині.

Рівняння прямої, що проходить через дві точки. Відомі координати двох точок на прямій : та (Рис. 2). Складемо рівняння прямої Вектор на прямій . лежить , отже, це напрямний вектор прямої .

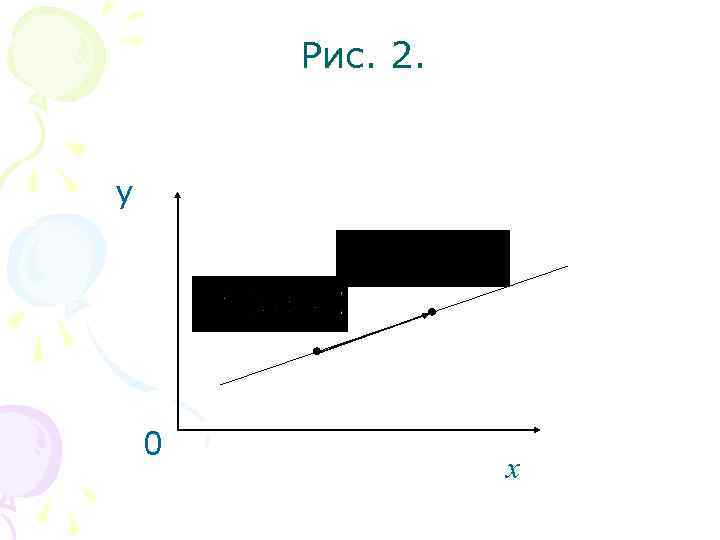Рис. 2. y 0 x

Якщо у канонічне рівняння прямої замість координат точки під- ставити координати точки , а замість координат цієї напрямного вектора підставити координати іншого напрямного вектора прямої – вектора , то одер- жимо рівняння прямої за двома точками: .

Рівняння прямої у відрізках на осях. - рівняння прямої у відрізках на осях, де - довжина відрізка на осі , а - довжина відрізка на осі .

Рівняння прямої, що проходить через задану точку перпендикулярно до даного вектора.

Загальне рівняння прямої та його частинні випадки

Дослідження загального рівняння прямої • Якщо , то рівняння або визначає пряму, паралельну осі Ох; • Якщо , то пряма визна- чає пряму, паралельну осі Оу;

• Якщо , то пряма виз- начає пряму, що проходить через початок координат; • Якщо , то пряма визна- чає вісь Ох; • Якщо чає вісь Оу;

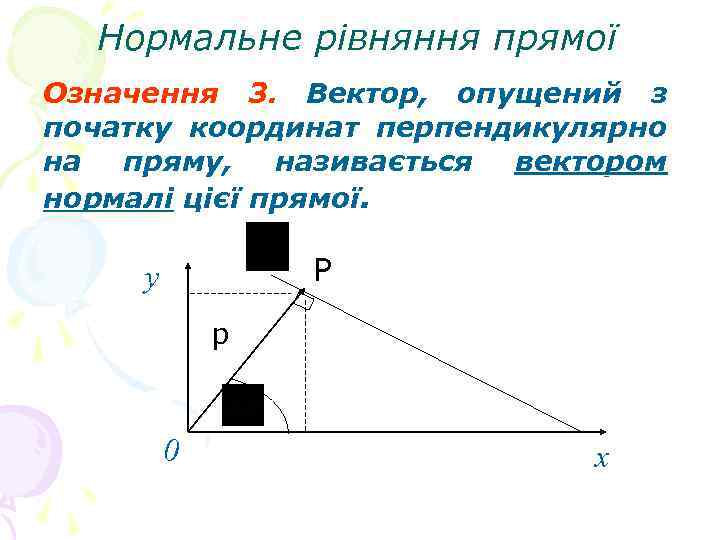Нормальне рівняння прямої Означення 3. Вектор, опущений з початку координат перпендикулярно на пряму, називається вектором нормалі цієї прямої. P y p 0 x

Hормальне рівняння прямої на площині

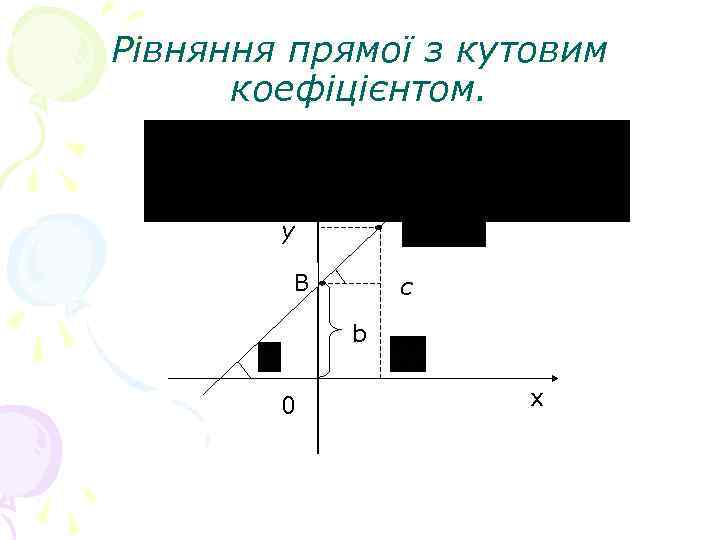Рівняння прямої з кутовим коефіцієнтом. y B c b 0 x

Рівняння прямої, що проходить через задану точку у вказаному напрямі.

2. Кут між двома прямими Кут між прямими, заданими канонічними рівняннями, визначається кутом між напрямними векторами цих прямих. Косинус кута між ними Звідси випливають умови паралельності і перпендикулярності прямих та : , .

Кут між прямими, заданими загальними рівняннями визначається кутом між нормальними векторами та цих прямих, тобто , звідки випливає, що

Кут між прямими, заданими рівняннями з кутовими коефіцієнтами , звідки визначається з рівності , . Отже, маємо , звідки випливають умови паралельності і перпендикулярності прямих :

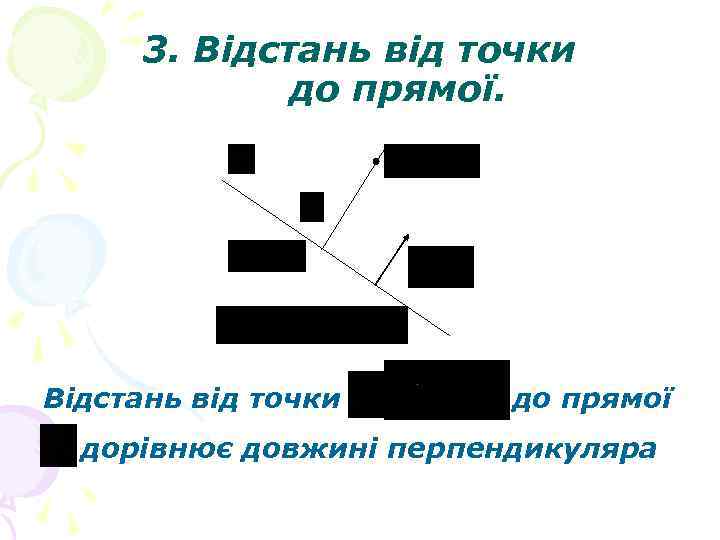3. Відстань від точки до прямої дорівнює довжині перпендикуляра

, опущеного з точки на пряму. Складемо рівняння прямої , як рівняння прямої, що проходить через дану точку паралельно до даного вектора : , звідки. Координати точки перетину прямих , як точки і задоволь- няють рівняння обох прямих, тобто систему рівнянь .

Після перетворень одержимо , , звідки відстань від точки. до прямої