Лекция 6 Тема 7 Методы принятия решений в

Лекция 6 Тема 7. Методы принятия решений в условиях полной определенности. Многокритериальная оптимизация

Тема 7. Методы принятия решений в условиях полной определенности. Многокритериальная оптимизация 7. 1. Принятие решения в условиях определенности. Целевая функция задачи принятия решения в условиях определенности. 7. 2. Многокритериальная оптимизация. Постановка задачи многокритериального выбора. • Типы многокритериальных задач. Основные проблемы при решении многокритериальных задач. • Требования к системе показателей (критериев). Понятие об оптимальных решениях. 7. 3. Критерий Парето. Выбор элементов множества Парето. Отношение Парето. 7. 4. Методы сужения множества Парето.

Типология управленческих решений относительно состояния среды • Принятие решения в условиях определенности • Принятие решения в условиях риска • Принятие решения в условиях неопределе нности • Принятие решения в условиях конфликта • 3

Выбор оптимального решения

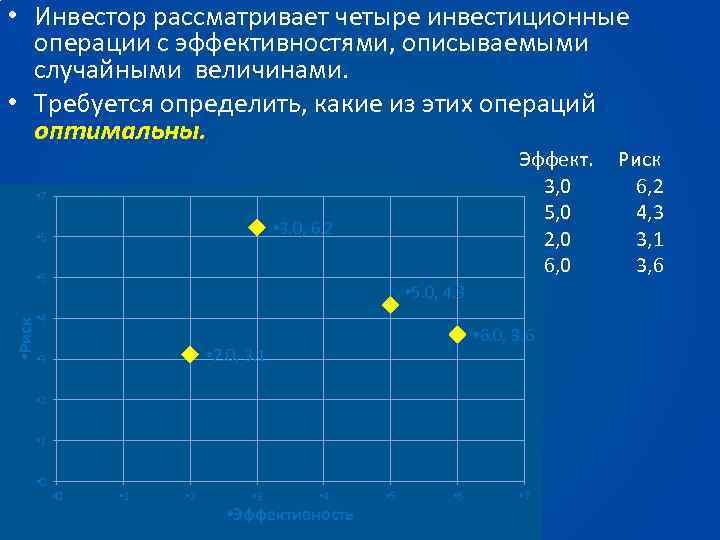• Инвестор рассматривает четыре инвестиционные операции с эффективностями, описываемыми случайными величинами. • Требуется определить, какие из этих операций оптимальны. Эффект. Риск 3, 0 6, 2 • 7 5, 0 4, 3 • 3. 0, 6. 2 • 6 2, 0 3, 1 6, 0 3, 6 • 5 • Риск • 5. 0, 4. 3 • 4 • 6. 0, 3. 6 • 2. 0, 3. 1 • 3 • 2 • 1 • 0 • 1 • 2 • 3 • 4 • Эффективность • 5 • 6 • 7

• Каждый из нас в ситуациях, требующих принятие решения, будь то на работе или дома, считает принятое решение наилучшим, и часто называет его оптимальным, не подозревая о том, что этот термин имеет глубокий математический смысл. Но как количественно оценить насколько принятое решение оптимально? • Если в бытовых ситуациях достаточно нашей интуиции и мнения близких, то оценка степени оптимальности решений в экономике, технике, общественной жизни и других отраслях человеческой деятельности требует более точных оценок.

Вторая половина 20 века характеризовалась резким ростом исследований в области поиска оптимальных решений в управлении. Среди фундаментальных результатов можно упомянуть, например, принцип максимума Понтрягина (Лев Семенович Понтрягин (1908— 1988) — советский математик, академик АН СССР) и метод динамического программирования Беллмана (Ричард Эрнст Беллман (1920 — 1984) —американский математик, специалист в области математики и вычислительной техники). Практическое применение эти методы находят, в основном, в системах управления сложными техническими объектами. При поиске оптимальных решений в экономике они используются реже. В экономике чаще применяется подход, предложенный итальянским мыслителем, социологом и экономистом Вильфредо Парето

Критерий Парето ПАРЕТО (Pareto) Вильфредо (1848 -1923) - итальянский мыслитель, социолог и экономист, внесший оригинальный вклад в экономическую теорию и социологическую науку. Сформулировал один из распространенных критериев оптимальности, предназначенный для того, чтобы проверить, улучшает ли предложенное изменение в экономике общий уровень благосостояния. “Следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит некоторым людям пользу (по их собственной оценке), является улучшением”.

7. 1. Принятие решения в условиях определенности • Принятие решения в условиях определенности характеризуется тем, что состояние среды является фиксированным, причем управляющая подсистема «знает» , в каком состоянии находится среда. • Пример: модели математического программирования, модели многокритериальной оптимизации, модели управления запасами и др. • 9

• Многокритериальная оптимизация— это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения.

7. 3. Критерий Парето. Выбор элементов множества Парето. Отношение Парето. • Состояние экономики S* считается лучшим по Парето, чем другое состояние S 1, если хотя бы один экономический субъект предпочитает S*, а все остальные по меньшей мере не делают различий между этими состояниями, но в то же время нет таких, кто предпочитает S 1 состоянию S*. • Критерий Парето неприменим к весьма распространенным ситуациям, при которых экономическое мероприятие, приносящее пользу одним, в то же время наносит ущерб другим.

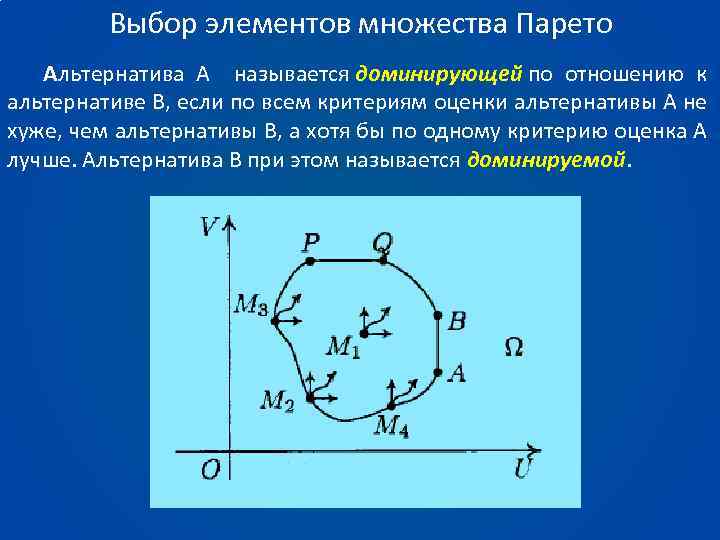Выбор элементов множества Парето Альтернатива А называется доминирующей по отношению к альтернативе В, если по всем критериям оценки альтернативы А не хуже, чем альтернативы В, а хотя бы по одному критерию оценка А лучше. Альтернатива В при этом называется доминируемой.

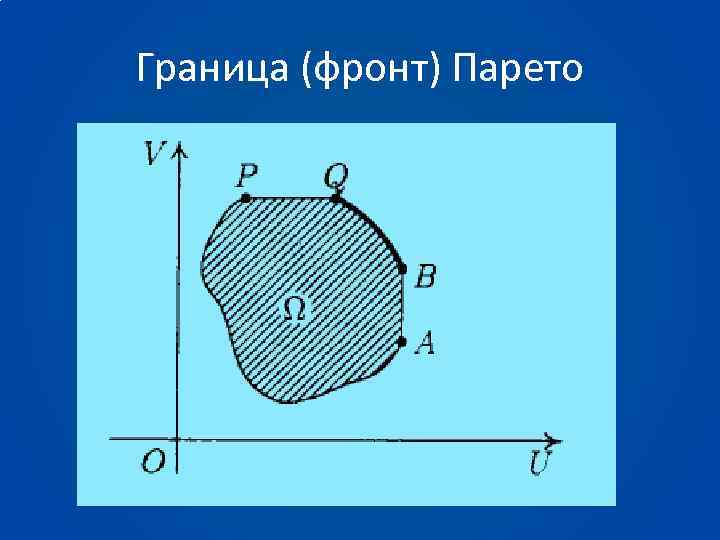Граница (фронт) Парето

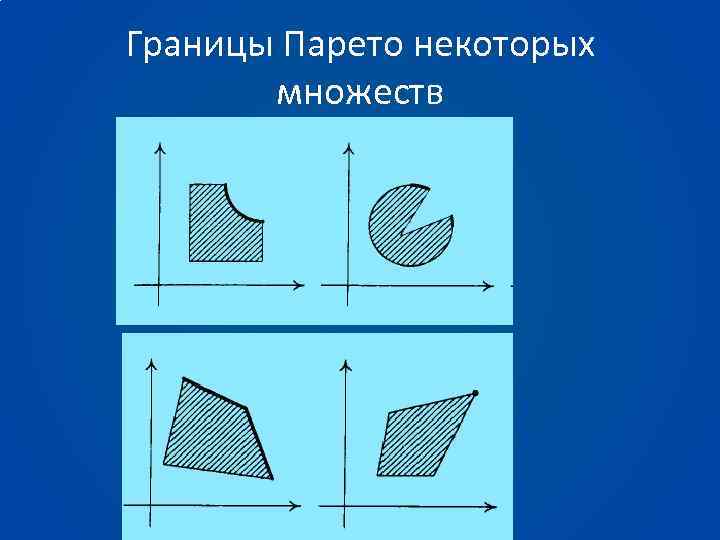Границы Парето некоторых множеств

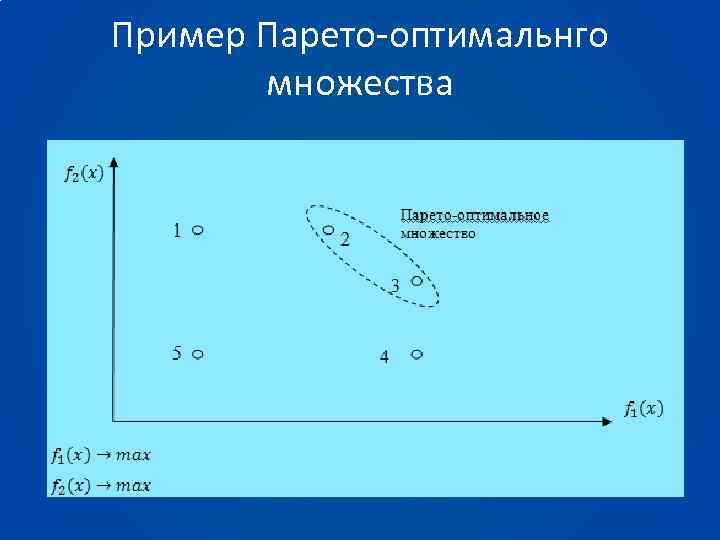Пример Парето-оптимальнго множества

Множество Парето • Альтернативы относятся к множеству Парето, если каждая из них превосходит любую другую по какому-то из критериев. Заметим, что эти критерии могут быть разными для разных альтернатив. • Альтернативы, принадлежащие к множеству Парето, называются несравнимыми. Их невозможно сравнить непосредственно на основе критериальных оценок. Они не находятся в отношении доминирования.

Отношение Парето • Объекты х и у находятся в отношении Парето Р (строгого предпочтения), если для всех критериев оценки хi ≥ уi, i = 1, m, и хотя бы по одному критерию j оценка xj > yj, j = 1, m. • Пример Установить отношения Парето для х, у, z, если х = (5, 5, 5, 5); у = (5, 4, 5, 5); z = (5, 5, 5, 4). • Сравнивая попарно критерии для всех альтернатив, получим х. Ру; x. Pz; y. Pz; z. Py.

Отношение несравнимости N • Объекты х и у находятся в отношении несравнимости N, если хотя бы по одному критерию i оценка хi > yi и найдется другой критерий j, для которого оценка хj < yj • Пример: х = (5, 8, 6, 5, 3, 3, 3); у = (3, 3, 3, 4, 9, 9, 9).

• Пример 1. Рассмотрим альтернативы со следующими оценками по двум критериям: (2, 3), (5, 3), (6, 4), (5, 5) (предполагается, что обе шкалы являются пропорциональными). Альтернатива (2, 3) не превосходит каждую другую альтернативу хотя бы по какому-то одному критерию; поскольку (2, 3) не превосходит (5, 3) ни по одному критерию, то, по определению множества Парето, (2, 3) не принадлежит множеству Парето). Альтернатива (5, 3) превосходит альтернативу (2, 3) по первому критерию, но не превосходит (6, 4) ни по одному критерию и, следовательно, также не входит в множества Парето. Следующая альтернатива (6, 4) превосходит (2, 3) и (5, 3) по обоим критериям и (5, 5) по первому критерию; поэтому она входит в множество Парето. Последняя альтернатива (5, 5) превосходит (2, 3) по обоим критериям и превосходит (5, 3) и (6, 4) по второму критерию; поэтому она входит в множество Парето. Таким образом, из альтернатив (2, 3), (5, 3), (6, 4), (5, 5) две последних – (6, 4) и (5, 5) – образуют множество Парето.

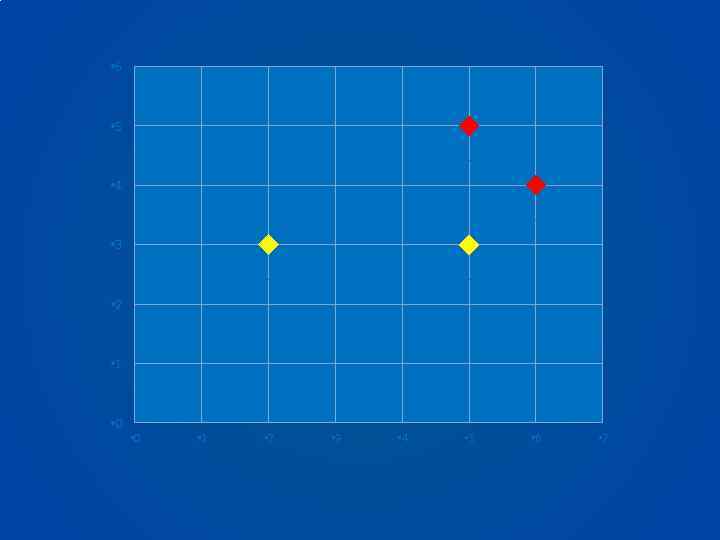• 6 • 5, 5 • 4 • 6, 4 • 3 • 2, 3 • 5, 3 • 2 • 1 • 0 • 1 • 2 • 3 • 4 • 5 • 6 • 7

Задача • Задача 1. Найти Парето-оптимальные альтернативы из множества альтернатив {(3, 7, 0), (4, 5, 1), (2, 3, 0), (3, 7, 3), (2, 6, 3), (4, 5, 2)} • Ответ: множество Парето состоит из альтернатив (3, 7, 3) и (4, 5, 2). • ( «Превосходит в чем-то всех остальных» )

7. 4. Методы сужения множества Парето 1. Аддитивная свертка критериев. 2. Принцип выделения главного критерия. Из совокупности локальных критериев выбирается один и принимается в качестве главного. К уровню других критериев предъявляется требование, чтобы они были не меньше некоторых заданных значений, образуя область, в которой ищется решение, наилучшее в смысле главного критерия.

3. Метод идеальной точки состоит в отыскании на границе Парето точки, ближайшей к точке утопии, задаваемой ЛПР. 4. Метод (последовательных) уступок заключается в том, что ЛПР. работая в режиме диалога со специалистом, анализирует точки на границе Парето и в конце концов соглашается остановиться на некоторой компромиссной.

Выводы по теме 7: 1. Целевая функция задачи принятия решения в условиях определенности представляет собой композицию функции реализации и оценочной функций. 2. Многокритериальная оптимизация— это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения. Каждая альтернатива удовлетворяет нескольким противоречивым требованиям и характеризуется несколькими показателями. 3. Критерий Парето является одним из распространенных критериев оптимальности при наличии в задаче принятия решений нескольких конфликтующих целевых функций.