Лекция 6 Солодухин Е А 1

Лекция № 6 Солодухин Е. А. 1

БАЗОВЫЕ ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ, ОСНОВАННЫЕ НА ПРЕОБРАЗОВАНИЙ ПРОЕКЦИЙ 2

• Преобразование прямой общего положения в прямую уровня (построение дополнительной проекции прямой на плоскости проекций ей параллельной). • Преобразование прямой в проецирующую прямую (построение дополнительной проекции прямой в виде точки). • Преобразование торсовой поверхности общего положения в проецирующую поверхность (построение дополнительной проекции торсовой поверхности в виде линии. • Построение дополнительной проекции плоской фигуры на параллельной ей плоскости проекций. 3

Практически рассматриваются всего два варианта преобразования. • Вариант 1. Переход от заданного положения объекта (прямой линии или плоской фигуры) в параллельное положение по отношению к выбранной плоскости проекций - выполняется только на основе прямоугольного варианта метода проецирования. • Вариант 2. Переход от заданного положения объекта (прямой линии или торсовой поверхности) в проецирующее положение по отношению к выбранной плоскости проекций - может быть выполнено на основе любого из рассмотренных вариантов метода проецирования. 4

Базовая задача № 1. Преобразование прямой общего положения в прямую уровня (построение дополнительной проекции прямой линии на параллельной ей плоскости проекций) 5

Задача может быть решена несколькими способами: • Переменой плоскостей проекций - подбором дополнительной плоскости проекций параллельной заданной прямой. • Плоскопараллельным перемещением прямой до положения параллельного одной из основных плоскостей проекций. • Поворотом прямой вокруг проецирующей прямой до положения параллельного одной из основных плоскостей проекций. 6

Решение задачи способом перемены плоскостей проекций. 7

(П 2 П 1) l (AB) - прямая общего положения 8

Подбирается дополнительная плоскость проекций П 4 ( П 4 || l ) (( П 4 П 1) (П 4 П 2)) На эпюре х14 || l 1 х24 || l 2 В качестве примера взята П 4 П 1 , следовательно, х14 || l 1 9

Строится дополнительная проекция l (AB) на поле плоскости П 4. А 1 А 4 х1, 4 и В 1 В 4 х1, 4 , (А 2 х1, 2) = (А 4 х1, 4) и (В 2 х1, 2) = (В 4 х1, 4) 10

Решение задачи способом плоскопараллельного перемещения 11

Плоскопараллельно переместить отрезок АВ до положения параллельного, например, фронтальной плоскости проекций. (А, П 1)=const А Г 1; А 1 Г 1; Г 1‖П 1 (А 2, х1, 2)= (А 21 , х1, 2) (B, П 1)=const В Г 2; В 1 Г 2; Г 2‖П 1 (В 2, х1, 2)= (В 21 , х1, 2) АВ =const ∠φ=((АВ)^П 1)=const (А 1 В 1)≌(А 11 В 11) Т. к. А 1 В 1‖П 2, то (А 11 В 11) ‖ х1, 2 12

13

Решение задачи способом вращения вокруг проецирующей прямой. 14

l (AB) - прямая общего положения 15

i – ось вращения. ( i П 1) ( i П 2 ) для примера взята (i П 1) ( B i ) (B ≡ B′ ) m – траектория перемещения точки А - окружность A m A′ m ; 16

А′В′ II П 2 А′ 1 В′ 1 II x 1, 2 17

Базовая задача № 2. Преобразование прямой общего положения в проецирующую прямую (построение дополнительной проекции прямой линии в виде точки) 18

Необходимо вспомнить, что: Прямая является проецирующей, если она проходит через центр проецирования. Для варианта параллельного метода проецирования прямая является проецирующей, если она параллельна направлению проецирования. Проекция проецирующей прямой вырождается в точку, и представляет собой точку пересечения самой прямой с плоскостью проекций. 19

Следовательно: • Чтобы прямую общего положения сделать проецирующей, необходимо центр проецирования совместить с прямой или саму прямую рассматривать как направление проецирования. • Чтобы построить дополнительную вырожденную проекцию проецирующей прямой в виде точки необходимо определить точку пересечения прямой с выбранной плоскостью проекций. 20

Преобразование прямой в проецирующую будет выполняться только на основе способа дополнительного проецирования: • центрального, • параллельного косоугольного, • перемены плоскостей проекций. 21

Построение дополнительной проекции прямой линии в виде точки на основе дополнительного центрального проецирования. 22

l - прямая общего положения 23

Задается центр дополнительного проецирования S′ S′ l Задается дополнительная плоскость проекций П′ В приведенном примере П′ П 1 24

Определяется точка пересечения прямой l с выбранной дополнительной плоскостью проекций П′ , которая является дополнительной проекцией l′ прямой l. l ∩ П′ = l′ l′ - точка 25

Построение дополнительной проекции прямой линии в виде точки на основе дополнительного параллельного косоугольного проецирования. 26

Отличие преобразования прямой общего положения в проецирующую на основе дополнительного параллельного косоугольного проецирования от дополнительного центрального проецирования состоит только в замене центра дополнительного проецирования, лежащего на прямой, на направление проецирования, инцидентного (совпадающего) этой прямой. 27

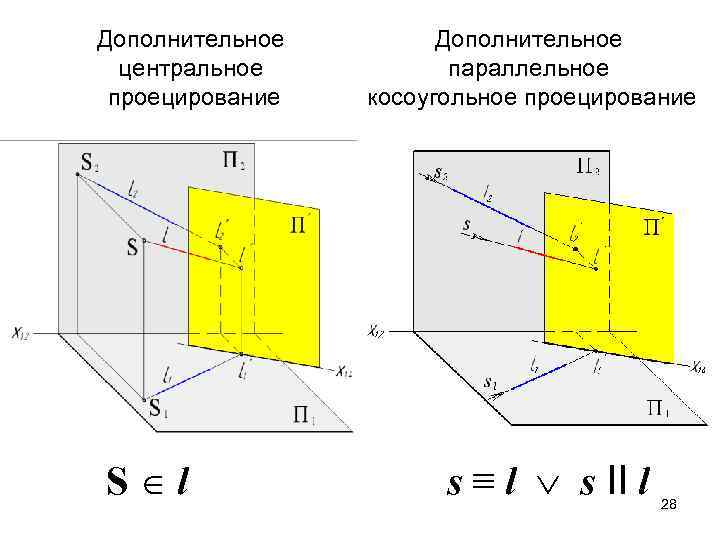Дополнительное центральное проецирование S l Дополнительное параллельное косоугольное проецирование s ≡ l s II l 28

Дополнительное центральное проецирование S l Дополнительное параллельное косоугольное проецирование s ≡ l s II l 29

Рассмотренные способы преобразования прямой общего положения в проецирующую прямую на основе центрального или параллельного косоугольного вариантов проецирования могут быть использованы только при решении позиционных задач. При решении метрических или конструктивных задач данное преобразование выполняется только на основе прямоугольного проецирования – например, способом перемены (замены) плоскостей проекций. 30

Построение дополнительной проекции прямой линии в виде точки на основе дополнительного прямоугольного проецирования – перемены (замены) плоскостей проекций 31

При прямоугольном проецировании прямая является проецирующей, если она перпендикулярна плоскости проекций. Следовательно, дополнительная плоскость проекций должна быть перпендикулярна заданной прямой П′ l , Но, так как l – прямая общего положения, то П′ – также является плоскостью общего положения и П′ П 1 и П′ П 2 , Следовательно, чтобы получить проекцию прямой линии общего положения в виде точки способом перемены плоскостей проекций, нельзя сразу подобрать необходимую плоскость проекций. Данное преобразование выполняется в два этапа. 32

1 -й этап Прямая преобразуется в прямую уровня ( П 4 II l ) ( П 4 П 1 П 4 П 2 ) Это рассмотренная ранее базовая задача № 1 на построение проекции прямой общего положения на плоскости проекций ей параллельной. 33

2 -й этап Из прямой уровня прямая преобразуется в проецирующую прямую ( П 5 l ) ( П 5 П 4 ) x 4, 5 A 4 B 4 (A 1 B 1 , x 1, 4) = (A 5 B 5 , x 4, 5) 34

Для прямой уровня данное преобразование выполняется за один этап Прямая уровня (h или f) параллельна плоскости проекций. Следовательно, если П′ (h или f), то П′ (П 1 или П 2), что удовлетворяет требования способа перемены плоскостей проекций. 35

Базовая задача № 3. Преобразование торсовой поверхности общего положения в проецирующую поверхность (построение проекции торсовой поверхности в виде линии) 36

Необходимо вспомнить, что: • • • Рассматриваемый нами метод проецирования является прямолинейным, т. е. все проецирующие линии прямые. Любая прямая, проходящая через центр проецирования, является проецирующей прямой и ее проекция вырождается в точку. В начертательной геометрии поверхность рассматривается как непрерывное множество последовательных положений образующей, перемещающейся в пространстве по определенному закону. Поверхность относится к классу линейчатых, если ее образующая прямая линия. Поверхность является проецирующей, если ее проекция при выбранном варианте метода проецирования вырождается в линию – кривую или 37 прямую.

Следовательно, при прямолинейном методе проецирования только линейчатая поверхность может стать проецирующей поверхностью, но при выполнении условия: все образующие поверхности должны быть проецирующими прямыми. Центр проецирования (реальная или несобственная точка), должен принадлежать этой поверхности (являться ее элементом) и принадлежать каждой образующей. Следовательно, все образующие поверхности должны пересекаться в одной точке (реальной или несобственной). 38

Сформулированному требованию отвечают только линейчатые торсовые поверхности – цилиндрическая, коническая и плоская (плоскость). Если точку пересечения образующих совместить с центром проецирования, то торсовая поверхность становится проецирующей. 39

Построение дополнительной проекции торсовой поверхности в виде линии на основе центрального и параллельного косоугольного проецирования 40

Дополнительную вырожденную проекцию торсовой поверхности в виде линии следует рассматривать как линию пересечения этой поверхности с выбранной плоскостью проекций. 41

′ = ∩ П′ d ; d П′ d = ∩ П′ d ≡ ′ 42

43

Построение дополнительной проекции плоскости общего положения в виде прямой линии способом перемены (замены) плоскостей проекций 44

(П 4 Т) (П 4 П 1 П 4 П 2) Если (П 4 Т), то (П 4 l l ⊂ Т) Если (l П 4) и (П 4 П 1 П 4 П 2) то (l II П 1 l II П 2) (l ≡ h) (l ≡ f ) Следовательно, если (П 4 П 1), то (П 4 h, h Т) и (x 1, 4 h 1) если (П 4 П 2), то (П 4 f, f Т) и (x 2, 4 f 2) 45

В качестве примера П 4 П 1 46

47

Базовая задача № 4. Построение проекции плоской фигуры на параллельной ей плоскости проекций 48

Решение задачи способом перемены (замены) плоскостей проекций 49

П′ II Т Так как плоскость Т – плоскость общего положения, то и любая плоскость ей параллельная, в том числе и проекций П′, также будет плоскостью общего положения, т. е. П′ П 1 и П′ П 2, что противоречит способу перемены (замены) плоскостей проекций. Следовательно, задача решается в два этапа. 1 -й этап. 2 -й этап. П 4 Т (базовая задача № 3). П 5 II Т. 50

1). П 4 Т( АВС), П 4 П 1 П 4 h 2). П 5 II Т( АВС), П 5 П 4 51

1) П 4 Т( АВС), П 4 П 1 П 4 h х1, 4 h 1 2) П 5 ‖ Т( АВС), П 5 П 4 х4, 5 ‖ Т 4 52

Решение задачи способом вращения вокруг прямой уровня 53

54

55