Лекция 06, ФЭТП, Тэттэр-Пономарев.ppt
- Количество слайдов: 27
 Лекция 6 r, L и r, C в цепях синусоидального тока. Комплексный метод расчета. Показательная и алгебраическая формы записи комплексных чисел. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
Лекция 6 r, L и r, C в цепях синусоидального тока. Комплексный метод расчета. Показательная и алгебраическая формы записи комплексных чисел. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 2 Активно-индуктивная цепь Второй закон Кирхгофа для мгновенных значений: (3. 22) Подставим (3. 4) в полученное уравнение. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
2 Активно-индуктивная цепь Второй закон Кирхгофа для мгновенных значений: (3. 22) Подставим (3. 4) в полученное уравнение. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 3 Преобразуем это уравнение с использованием известных математических приемов: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
3 Преобразуем это уравнение с использованием известных математических приемов: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 4 На основе полученного результата: (3. 26) (3. 27) Величина называется полным сопротивлением. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
4 На основе полученного результата: (3. 26) (3. 27) Величина называется полным сопротивлением. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 5 Полное сопротивление z содержит в своем составе активное сопротивление r. Это сопротивление отличается по величине от сопротивления, измеренного на постоянном токе в силу поверхностного эффекта. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
5 Полное сопротивление z содержит в своем составе активное сопротивление r. Это сопротивление отличается по величине от сопротивления, измеренного на постоянном токе в силу поверхностного эффекта. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 Поверхностный эффект 6 Плотность переменного тока по сечению проводника распределяется неравномерно. Максимальные значения плотности тока имеют место у поверхности проводника; минимальные – на оси проводника. Вследствие этого сопротивление проводника увеличивается по сравнению со случаем постоянного тока. Проявление поверхностного эффекта тем больше, чем больше частота тока. Сопротивления, измеренные при нулевой частоте (постоянный ток) и при 50 Гц отличаются мало. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
Поверхностный эффект 6 Плотность переменного тока по сечению проводника распределяется неравномерно. Максимальные значения плотности тока имеют место у поверхности проводника; минимальные – на оси проводника. Вследствие этого сопротивление проводника увеличивается по сравнению со случаем постоянного тока. Проявление поверхностного эффекта тем больше, чем больше частота тока. Сопротивления, измеренные при нулевой частоте (постоянный ток) и при 50 Гц отличаются мало. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 7 Входящее в состав полного сопротивления z индуктивное сопротивление х. L, равное ωL, относится к разряду реактивных сопротивлений. Активное сопротивление r связано с потерями электрической энергии. Реактивное сопротивление x. L определяется обратимыми процессами преобразования энергии магнитного поля (нет потерь электрической энергии). Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
7 Входящее в состав полного сопротивления z индуктивное сопротивление х. L, равное ωL, относится к разряду реактивных сопротивлений. Активное сопротивление r связано с потерями электрической энергии. Реактивное сопротивление x. L определяется обратимыми процессами преобразования энергии магнитного поля (нет потерь электрической энергии). Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 Основы комплексного (символического) метода расчета электрических цепей синусоидального тока 8 Соотношения для мгновенных значений напряжений и токов неудобны для расчета сложных цепей (громоздкие выражения, большой объем вычислений). Упрощение расчетов достигается переходом к комплексным числам и соотношениям в комплексной форме. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
Основы комплексного (символического) метода расчета электрических цепей синусоидального тока 8 Соотношения для мгновенных значений напряжений и токов неудобны для расчета сложных цепей (громоздкие выражения, большой объем вычислений). Упрощение расчетов достигается переходом к комплексным числам и соотношениям в комплексной форме. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 Комплексное число можно представить в различных формах: 9 где: В основу рассуждений положим равенство: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
Комплексное число можно представить в различных формах: 9 где: В основу рассуждений положим равенство: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 10 Рассмотрим вектор, вращающийся с постоянной угловой скоростью ω на комплексной плоскости Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
10 Рассмотрим вектор, вращающийся с постоянной угловой скоростью ω на комплексной плоскости Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 11 Проекции вращающегося вектора на оси действительных и мнимых значений: (3. 38) где Величину называют комплексной амплитудой. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
11 Проекции вращающегося вектора на оси действительных и мнимых значений: (3. 38) где Величину называют комплексной амплитудой. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 12 Дифференцирование и интегрирование (3. 38) приводит к соотношениям: (3. 40) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
12 Дифференцирование и интегрирование (3. 38) приводит к соотношениям: (3. 40) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 13 Очевидны следующие свойства (3. 38): суммированию векторов соответствует суммирование их проекций; умножению вектора на постоянный множитель соответствует умножение его проекций на тот же множитель. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
13 Очевидны следующие свойства (3. 38): суммированию векторов соответствует суммирование их проекций; умножению вектора на постоянный множитель соответствует умножение его проекций на тот же множитель. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 14 Между мнимой частью уравнения (3. 38) слева и комплексной амплитудой справа существует однозначное соответствие: (3. 41) Следовательно, операции с синусоидальными функциями можно заменить операциями с комплексными числами. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
14 Между мнимой частью уравнения (3. 38) слева и комплексной амплитудой справа существует однозначное соответствие: (3. 41) Следовательно, операции с синусоидальными функциями можно заменить операциями с комплексными числами. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 15 Для производной и интеграла: (3. 42) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
15 Для производной и интеграла: (3. 42) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 16 При расчете электрических цепей используются комплексные амплитуды напряжения, тока, ЭДС: При этом имеют место следующие соответствия: (3. 43) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
16 При расчете электрических цепей используются комплексные амплитуды напряжения, тока, ЭДС: При этом имеют место следующие соответствия: (3. 43) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 17 Для активно-индуктивной цепи справедливо уравнение (3. 22): Запишем это уравнение в комплексной форме, используя понятие комплексных амплитуд: (3. 45) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
17 Для активно-индуктивной цепи справедливо уравнение (3. 22): Запишем это уравнение в комплексной форме, используя понятие комплексных амплитуд: (3. 45) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 18 где комплексное сопротивление цепи – (сопротивление цепи в комплексной форме). Величина называется индуктивным сопротивлением в комплексной форме. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
18 где комплексное сопротивление цепи – (сопротивление цепи в комплексной форме). Величина называется индуктивным сопротивлением в комплексной форме. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 Комплексное сопротивление Z записывается и в показательной форме: 19 где установленное ранее полное сопротивление. Полное сопротивление z – модуль комплексного сопротивления Z; φ – угол сдвига фаз между напряжением и током. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
Комплексное сопротивление Z записывается и в показательной форме: 19 где установленное ранее полное сопротивление. Полное сопротивление z – модуль комплексного сопротивления Z; φ – угол сдвига фаз между напряжением и током. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 20 Итогом решения является комплексная амплитуда тока: По комплексной амплитуде тока легко записывается мгновенное значение тока: где Im – мнимая часть. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
20 Итогом решения является комплексная амплитуда тока: По комплексной амплитуде тока легко записывается мгновенное значение тока: где Im – мнимая часть. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
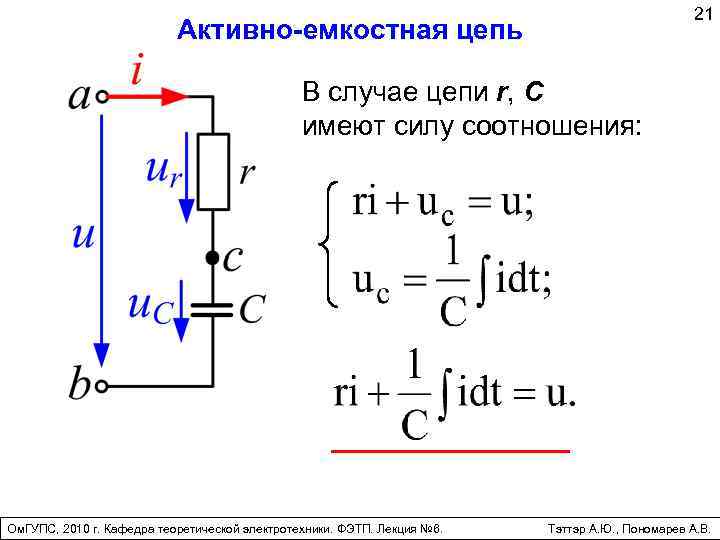 21 Активно-емкостная цепь В случае цепи r, C имеют силу соотношения: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
21 Активно-емкостная цепь В случае цепи r, C имеют силу соотношения: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 Уравнение для комплексных амплитуд: 22 где Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
Уравнение для комплексных амплитуд: 22 где Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 23 Здесь снова полное сопротивление активно-емкостной цепи; угол сдвига фаз. Комплексная амплитуда тока: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
23 Здесь снова полное сопротивление активно-емкостной цепи; угол сдвига фаз. Комплексная амплитуда тока: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 24 Параметр представляет емкостное сопротивление в комплексной форме. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
24 Параметр представляет емкостное сопротивление в комплексной форме. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 25 В операциях с комплексными числами полезно понимание следующих соотношений: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
25 В операциях с комплексными числами полезно понимание следующих соотношений: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 Например, емкостное сопротивление записывается в двух формах: 26 т. е. использовалось правило: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
Например, емкостное сопротивление записывается в двух формах: 26 т. е. использовалось правило: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
 27 Равенство показывает, что умножение комплекса на j определяет поворот соответствующего этому комплексному числу вектора на 90º в положительном направлении, т. е. против часовой стрелки. Умножению на соответствует поворот вектора на 90º в отрицательном направлении (по часовой стрелке). Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.
27 Равенство показывает, что умножение комплекса на j определяет поворот соответствующего этому комплексному числу вектора на 90º в положительном направлении, т. е. против часовой стрелки. Умножению на соответствует поворот вектора на 90º в отрицательном направлении (по часовой стрелке). Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 6. Тэттэр А. Ю. , Пономарев А. В.


