Лекция 6. Производство и технология Модуль 3. Теория

Лекция 6. Производство и технология Модуль 3. Теория производства Микроэкономика

Рассматриваемые вопросы 1. Технология производства и технологические ограничения. 2. Производственная функция. 2. 1. Свойства производственной функции. 2. 2. Основные характеристики производственных функций. 2. 3. Виды производственной функции 3. Валовой, средний и предельный продукт 3. 1 Взаимосвязь валового среднего и предельного продуктов 4. Изокванта и предельная норма технологического замещения. 5. Примеры технологий и виды изоквант. 6. Эффект масштаба.

1. Технология производства и технологические ограничения. Производство – процесс использования рабочей силы и оборудования в сочетании с природными ресурсами и материалами для изготовления необходимых товаров и услуг p Факторы процесса производства – производственные услуги труда, капитала и природных ресурсов p Технология – практические знания о производстве товаров и услуг p

2. Производственная функция. ПФ – количественная взаимосвязь между факторами производства и выпуском продукции Q = F(L, K) L- труд, рабочая сила К – капитал, основные фонды

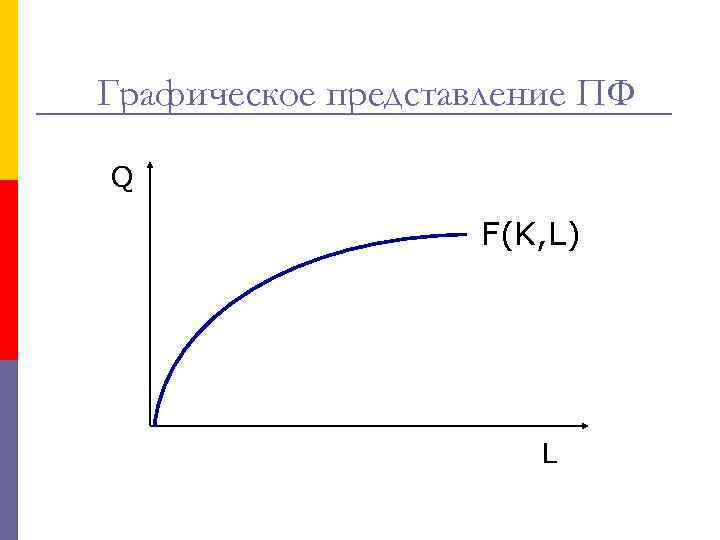Графическое представление ПФ Q F(K, L) L

2. 1. Свойства производственной функции.

2. 2. Основные характеристики производственных функций.

2. 3. Виды производственной функции 1. ПФ с фиксированными пропорциями Q = min {m. L, n. K} 2. Линейная производственная функция Q =a. L+b. K 3. Функция Кобба-Дугласа Q = A K Lβ

3. Валовой, средний и предельный продукты

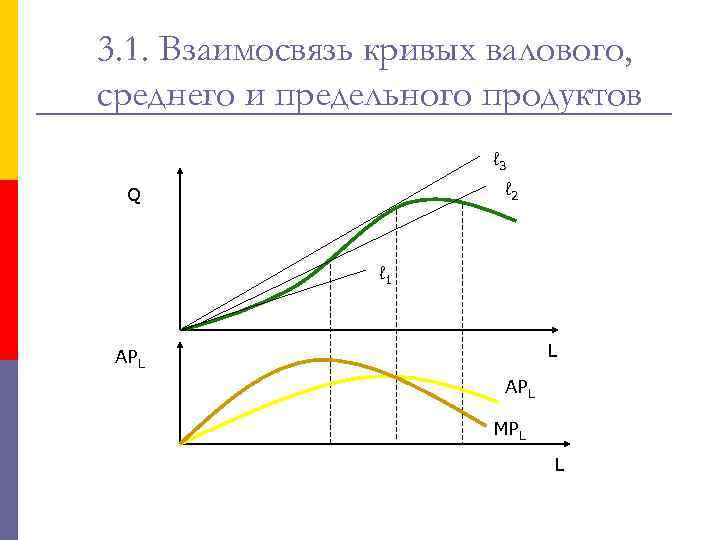3. 1. Взаимосвязь кривых валового, среднего и предельного продуктов ℓ 3 ℓ 2 Q ℓ 1 L APL АРL MPL L

4. Изокванта и предельная норма технологического замещения. p Изокванта – множество всех возможных комбинаций факторов производства (K, L), которые достаточны для производства данного объема выпуска (Q) p Предельная норма технологического замещения (MRTS) – наклон изокванты ∆Q = MPl ∆L +MPK∆K =0

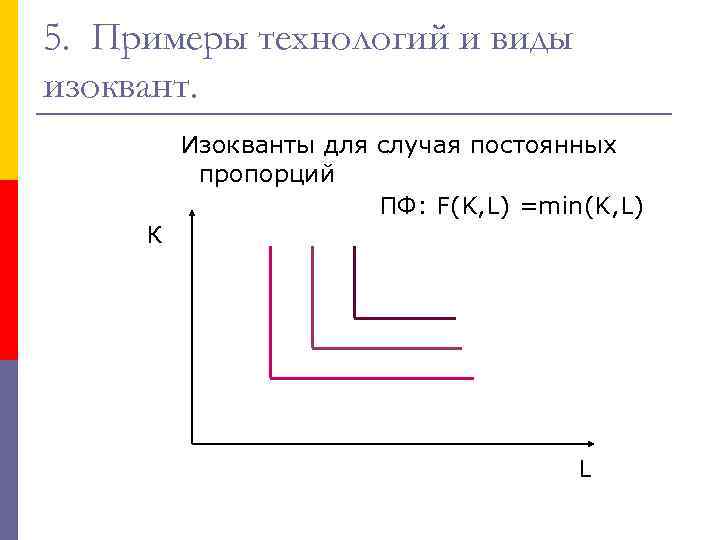5. Примеры технологий и виды изоквант. Изокванты для случая постоянныx пропорций ПФ: F(K, L) =min(K, L) К L

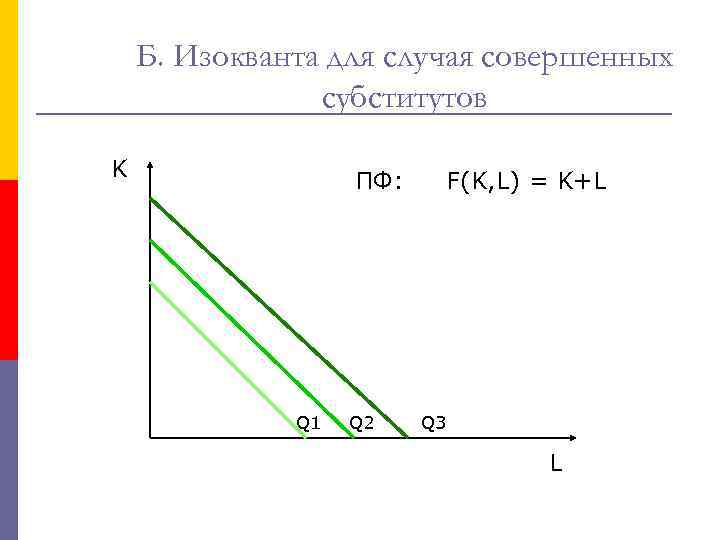Б. Изокванта для случая совершенных субститутов K ПФ: Q 1 Q 2 F(K, L) = K+L Q 3 L

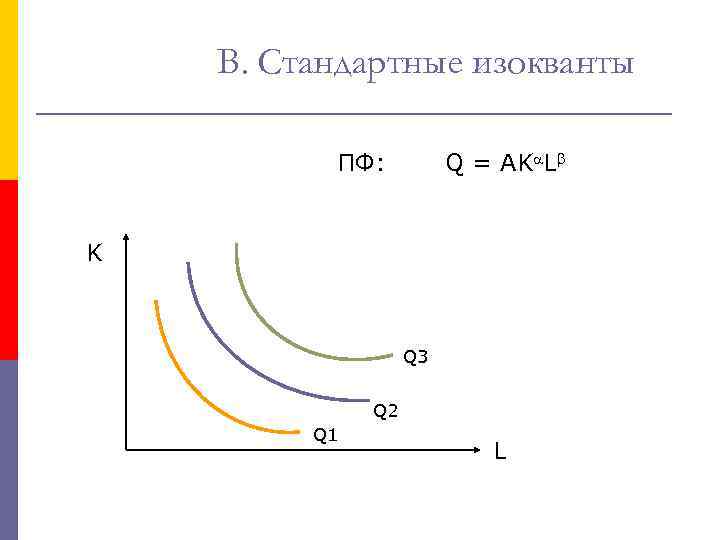В. Стандартные изокванты ПФ: Q = AK L K Q 3 Q 2 Q 1 L

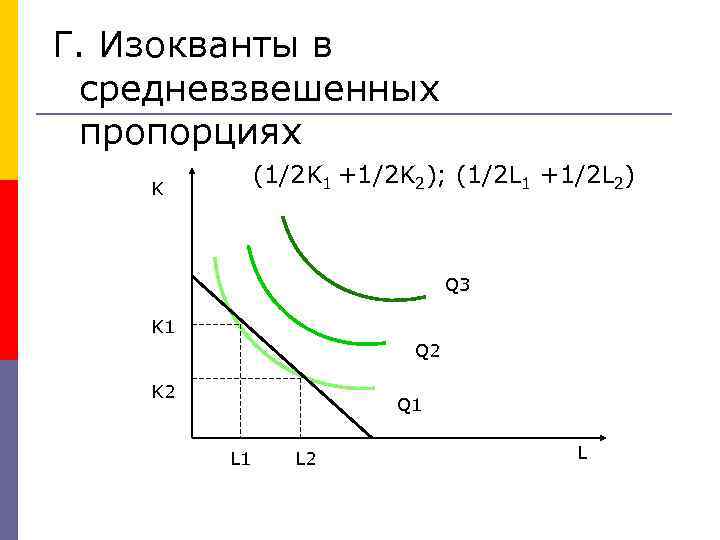Г. Изокванты в средневзвешенных пропорциях (1/2 K 1 +1/2 K 2); (1/2 L 1 +1/2 L 2) K Q 3 K 1 Q 2 K 2 Q 1 L 2 L

6. Эффект масштаба. А. Постоянная отдача от масштаба F(K, L) = F( K, L Б. Возрастающая отдача от масштаба F(K, L) > F( K, L) В. Убывающая отдача от масштаба F(K, L) < F( K, L)

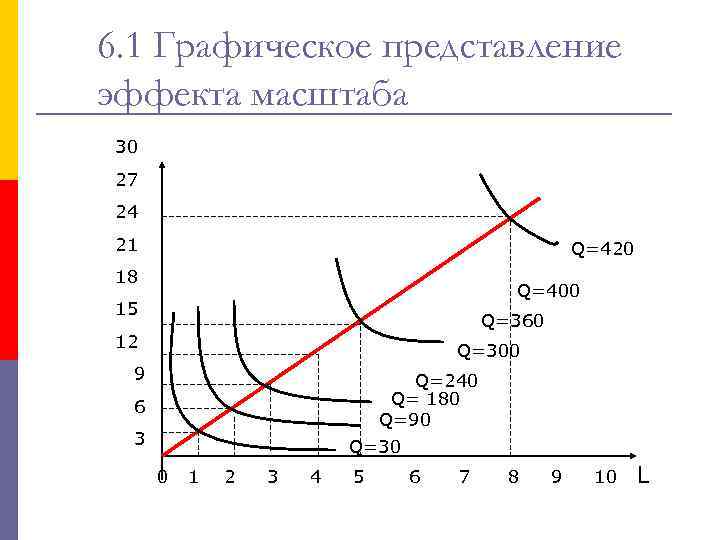6. 1 Графическое представление эффекта масштаба 30 27 24 21 Q=420 18 Q=400 15 Q=360 12 Q=300 9 Q=240 Q= 180 Q=90 6 3 Q=30 0 1 2 3 4 5 6 7 8 9 10 L

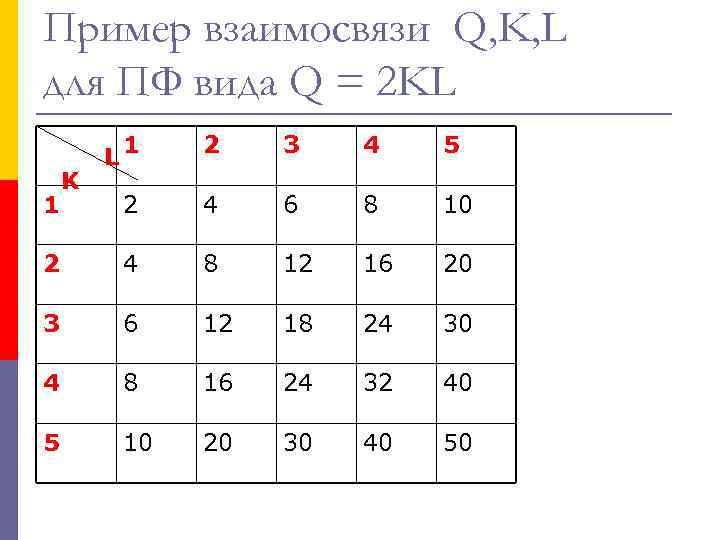Пример взаимосвязи Q, K, L для ПФ вида Q = 2 KL 1 2 3 4 5 2 4 6 8 10 2 4 8 12 16 20 3 6 12 18 24 30 4 8 16 24 32 40 5 10 20 30 40 50 1 K L