Лекция 6 Модуль I Электрические цепи синусоидального тока

Лекция 6 Модуль I. Электрические цепи синусоидального тока (продолжение).

Содержание 1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений i = Im sin(ωt+ψi) или По второму закону Кирхгофа для заданной цепи: или

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). Здесь - комплексное полное сопротивление цепи с тремя последовательно соединенными элементами. Модуль комплексного полного сопротивления: где – реактивное сопротивление цепи. Аргумент комплексного полного сопротивления

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). Действующее значение тока: Начальная фаза тока: или Действующие значения тока и напряжения в этой цепи определяется полным сопротивлением Z в форме закона Ома. По фазе напряжение опережает ток на угол φ. При этом полное сопротивление и разность фаз определяются соотношением сопротивлений трех элементов

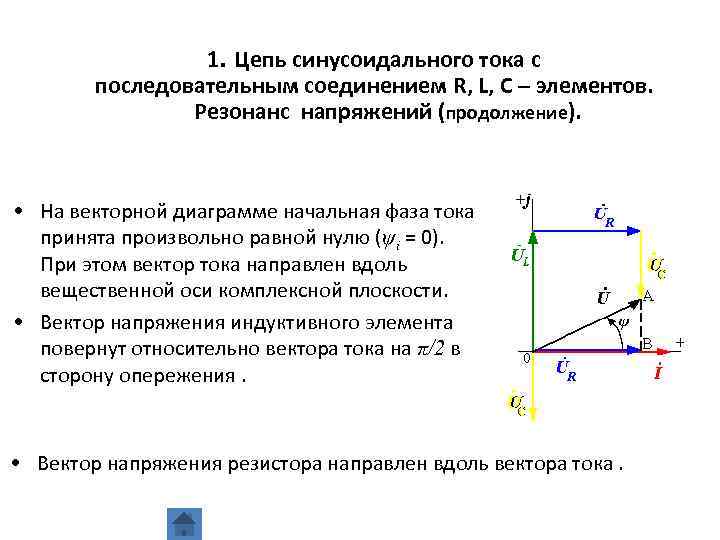1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • На векторной диаграмме начальная фаза тока принята произвольно равной нулю (ψi = 0). При этом вектор тока направлен вдоль вещественной оси комплексной плоскости. • Вектор напряжения индуктивного элемента повернут относительно вектора тока на π/2 в сторону опережения. • Вектор напряжения резистора направлен вдоль вектора тока.

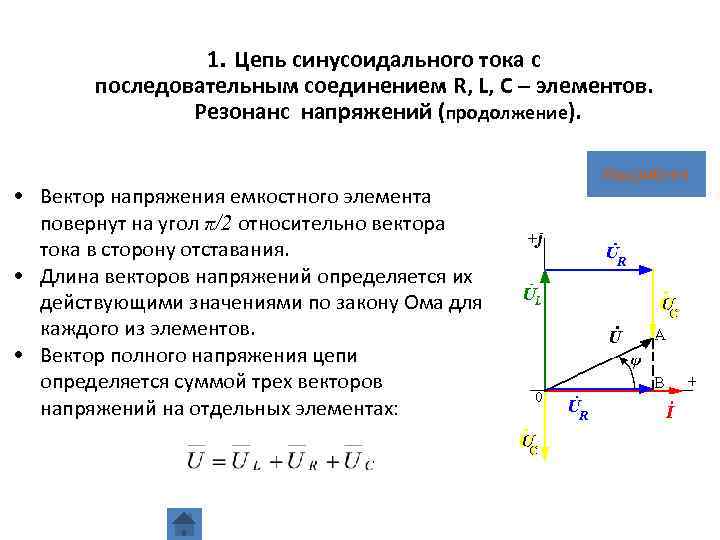1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Вектор напряжения емкостного элемента повернут на угол π/2 относительно вектора тока в сторону отставания. • Длина векторов напряжений определяется их действующими значениями по закону Ома для каждого из элементов. • Вектор полного напряжения цепи определяется суммой трех векторов напряжений на отдельных элементах: Подробней

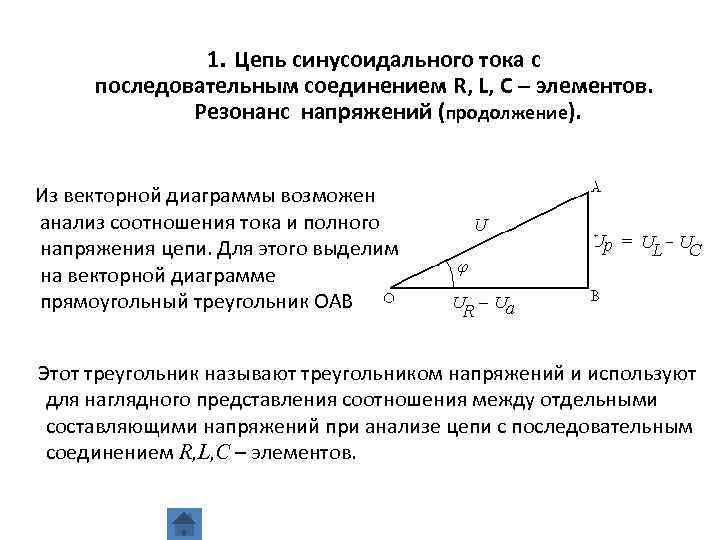1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). Из векторной диаграммы возможен анализ соотношения тока и полного напряжения цепи. Для этого выделим на векторной диаграмме прямоугольный треугольник ОАВ Этот треугольник называют треугольником напряжений и используют для наглядного представления соотношения между отдельными составляющими напряжений при анализе цепи с последовательным соединением R, L, C – элементов.

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). Поделим стороны треугольника напряжений на величину тока I. При этом получается подобный треугольник Этот треугольник называют треугольником сопротивлений и используют для наглядного представления соотношения между сопротивлениями отдельных элементов и полным сопротивлением цепи с последовательным соединением R, L, C – элементов.

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). По теореме Пифагора для треугольника сопротивлений модуль полного сопротивления: Из того же треугольника разность фаз для всей цепи:

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). Аналогичным образом можно определять комплексное полное сопротивление участка цепи, содержащего два других идеальных элемента, или один из них.

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). Для анализа энергетических соотношений в цепи с последовательным соединением R, L, C – элементов определим характер изменения мгновенной мощности в этой цепи: Перейдя к действующим значениям напряжения и тока

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Мощность в рассматриваемой цепи изменяется во времени по гармоническому закону с двойной частотой. При этом колебания мощности происходят вокруг среднего значения, определяемого первым слагаемым в правой части выражения. • Среднее значение мощности определяет активную мощность. или Активная мощность определяется мощностью резистора

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Произведение действующих значений тока и полного напряжения цепи называют полной мощностью S: Единица полной мощности – ВА, к. ВА, МВА. • Соотношение активной и полной мощностей: или • Отношение активной мощности к полной называется коэффициентом мощности. Коэффициент мощности обозначают cosφ.

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Коэффициент мощности можно определить соотношением сопротивлений отдельных элементов, например, исходя из треугольника сопротивлений: • Графически соотношение активной и полной мощности отображается треугольником мощностей.

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Нижний катет треугольника пропорционален активной мощности: • Правый катет треугольника пропорционален величине: Это реактивная мощность всей цепи. • Гипотенуза треугольника оказывается равной полной мощности: • Из треугольника мощностей: или

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Комплексное значение полной мощности • Здесь сопряженный комплексный ток. Тогда:

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). В рассматриваемой цепи при разном соотношении сопротивлений элементов (R, XL, XC) создается разный режим работы. При этом характер цепи определяется разностью фаз φ, значения которой могут быть положительными или отрицательными в диапазоне от π/2 до – π/2. Векторная диаграмма построена в предположении, что индуктивное сопротивление больше емкостного (ХL> ХC ). Реактивное сопротивление всей цепи положительно:

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • При этом в соответствии с законом Ома напряжение на индуктивном элементе больше емкостного: • Разность фаз всей цепи оказывается положительной, т. е. полное напряжение опережает по фазе ток на угол φ, больший нуля: Треугольник сопротивлений и треугольник мощностей для этого режима имеют вид, рассмотренный ранее

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • В этом режиме цепь характеризуется активной мощностью P и положительной реактивной мощностью Q > 0. Положительное значение реактивной мощности свидетельствует о том, что индуктивная мощность больше емкостной, т. е. индуктивный элемент преобладает над емкостным элементом. • В этом режиме характер цепи называют активно–индуктивным.

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • При ХL < ХC реактивное сопротивление всей цепи отрицательно: • В соответствии с законом Ома напряжение на индуктивном элементе меньше емкостного: • Разность фаз всей цепи оказывается отрицательной, т. е. полное напряжение отстает по фазе от тока:

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Треугольник сопротивлений и треугольник мощностей для этого режима • В этом режиме цепь характеризуется активной мощностью P и отрицательной реактивной мощностью Q<0. Отрицательное значение реактивной мощности свидетельствует о том, что индуктивная мощность меньше емкостной, т. е. емкостный элемент преобладает над индуктивным элементом. В этом режиме характер цепи называют активно–емкостным.

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • При ХL = ХC. Реактивное сопротивление всей цепи оказывается равным нулю: • В соответствии с законом Ома напряжения на индуктивном и емкостном элементах равны между собой: • Разность фаз всей цепи оказывается равной нулю, т. е. полное напряжение совпадает по фазе с током:

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Треугольник сопротивлений и треугольник мощностей для этого режима вырождаются в отрезок, поскольку один катет становится равным нулю. • В этом режиме цепь характеризуется активной мощностью P. Реактивная мощность равна нулю Q = 0. При этом активная мощность равна полной мощности: P = S = UI, а коэффициент мощности равен:

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Отсутствие реактивной мощности при наличии в цепи индуктивного и емкостного элементов свидетельствует о том, что реактивная индуктивная мощность и реактивная емкостная мощность взаимно компенсируются. При этом цепь имеет активный характер, поскольку обладает лишь активной мощностью. • Явление, возникающее в неразветвленной цепи с элементами L, R, C, когда полное напряжение и ток совпадают по фазе, называется резонансом напряжений. • Условие резонанса напряжений: ХL = ХC или

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Создать резонанс напряжений в цепи можно изменяя параметры L или С при неизменной частоте, или изменяя частоту при заданных параметрах L и С. • На рисунке в точке A ХL = ХС. При этом полное сопротивление минимально и определяется лишь активным сопротивлением резистора: • Эта точка определяет резонансную частоту:

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). • Ток цепи в этом режиме наибольший: • Активная мощность определяется величиной резонансного тока: Аналогичным образом возникает режим резонанс напряжений при неизменной частоте и изменении индуктивности индуктивного элемента, либо емкости емкостного элемента.

1. Цепь синусоидального тока с последовательным соединением R, L, C – элементов. Резонанс напряжений (продолжение). Признаком резонанса напряжений в цепи является максимальное значение тока и активной мощности • Резонанс напряжений используется в радиотехнических цепях при построении схем резонансных фильтров. При этом свойства цепи оказываются различными для сигналов разных частот. • В электротехнических установках частота неизменна. Здесь возникновение резонанса напряжений обусловлено изменением параметров элементов. При ХL = ХС > R при резонансе напряжений возможны перенапряжения на отдельных участках цепи.

Заключение 1. В цепи синусоидального тока с последовательным соединением R, L, C – элементов соотношение между током и напряжением по величине: Полное сопротивление цепи Разность фаз всей цепи с тремя элементами определяется соотношением параметров отдельных элементов: Соотношение между комплексными током и напряжением соответствует закону Ома: Полное комплексное сопротивление

Заключение 2. Полная мощность в цепи с тремя элементами: Отношение активной мощности к полной называется коэффициентом мощности: 3. Характер цепи в разных режимах работы определяется соотношением параметров ее элементов. При равенстве индуктивного и емкостного сопротивлений возникает резонанс напряжений. В этом режиме полное сопротивление равно активному ток цепи максимален, разность фаз равна нулю коэффициент мощности т. е. активная мощность равна полной мощности.

Контрольные вопросы Установите соответствие между элементами Параметры элементов участка цепи: R=40 Ом, XL =50 Ом, XC =20 Ом. Модуль полного сопротивления участка цепи Z равен. . . Ом.

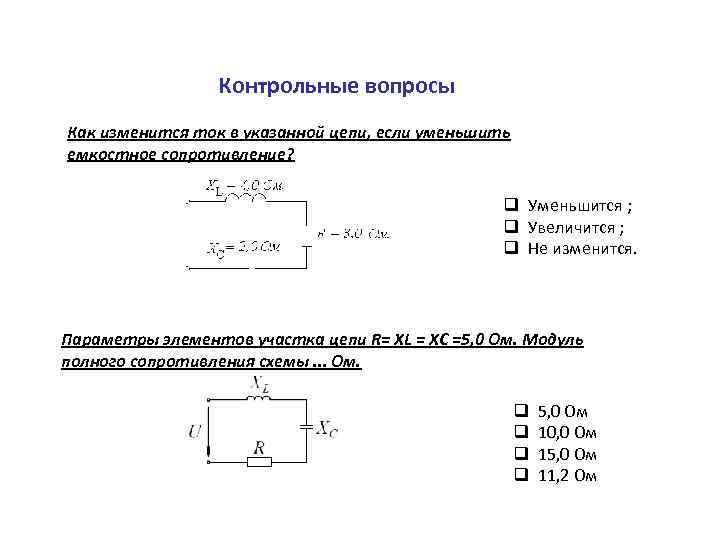Контрольные вопросы Как изменится ток в указанной цепи, если уменьшить емкостное сопротивление? q Уменьшится ; q Увеличится ; q Не изменится. Параметры элементов участка цепи R= XL = XC =5, 0 Ом. Модуль полного сопротивления схемы. . . Ом. q q 5, 0 Ом 10, 0 Ом 15, 0 Ом 11, 2 Ом

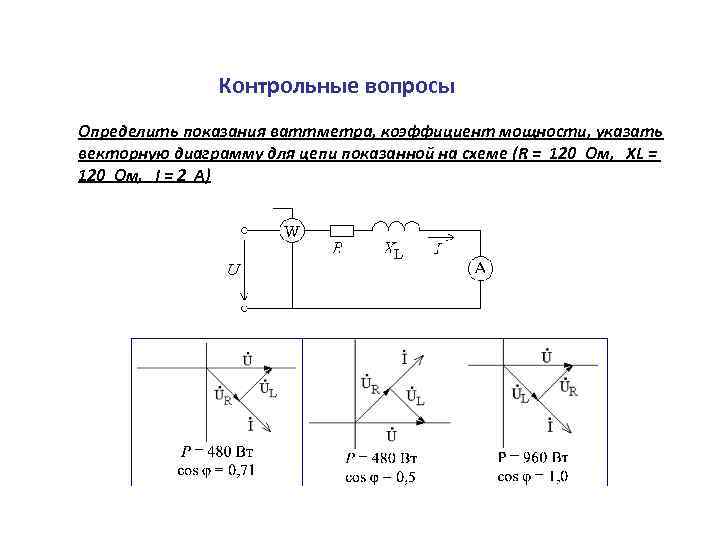Контрольные вопросы Определить показания ваттметра, коэффициент мощности, указать векторную диаграмму для цепи показанной на схеме (R = 120 Ом, XL = 120 Ом, I = 2 А)

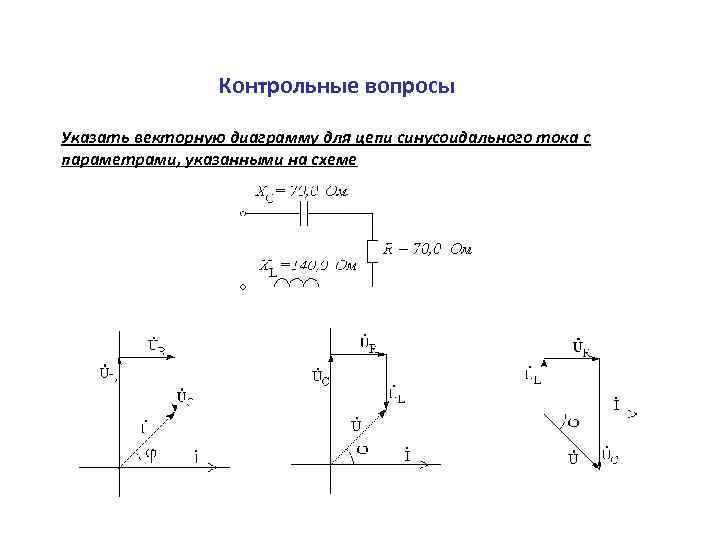Контрольные вопросы Указать векторную диаграмму для цепи синусоидального тока с параметрами, указанными на схеме

Контрольные вопросы Каким должно быть индуктивное сопротивление в предложенной цепи для создания режима резонанс напряжений? q q q XL = XL = 45 Ом; 35 Ом; 10 Ом; 0; 80 Ом. В цепи синусоидального тока активная мощность P=800 Вт, реактивная мощность Q=600 ВАр. Определить полную мощность и коэффициент мощности.