Лекция 6 Криволинейный интеграл первого рода 1 Определение

Лекция 6 Криволинейный интеграл первого рода 1. Определение криволинейного интеграла первого рода 2. Вычисление криволинейного интеграла первого рода 1

1. Определение криволинейного интеграла первого рода Определение Кривая L называется гладкой, если непрерывны на и имеют непрерывные производные, не обращающиеся одновременно в ноль (т. е. кривая в каждой точке имеет касательную, направление которой непрерывно зависит от точки касания) 2

Рассмотрим интеграл по фигуре в случае Пусть дуга AB кривой L – гладкая или кусочногладкая (составлена из конечного числа гладких кусков). - криволинейный интеграл первого рода 3

Приведем полученный интеграл к определенному. Введем параметр для кривой AB – длину дуги l, отсчитываемую от начальной точки. - параметрические уравнения кривой AB Поставим в соответствие 4

из равенства интегральных сумм 5

Замечания 1. - длина дуги Знак не зависит от того, какая точка кривой AB считается начальной, а какая конечной. Ориентация кривой AB (выбор направления) на величину криволинейного интеграла I рода 6 не влияет.

2. Если функция f(x, y) непрерывна вдоль гладкой кривой AB , то существует криволинейный интеграл Следует из (2), т. к. при данных условиях существует определенный интеграл справа, а оба интеграла либо существуют, либо не существуют одновременно. 7

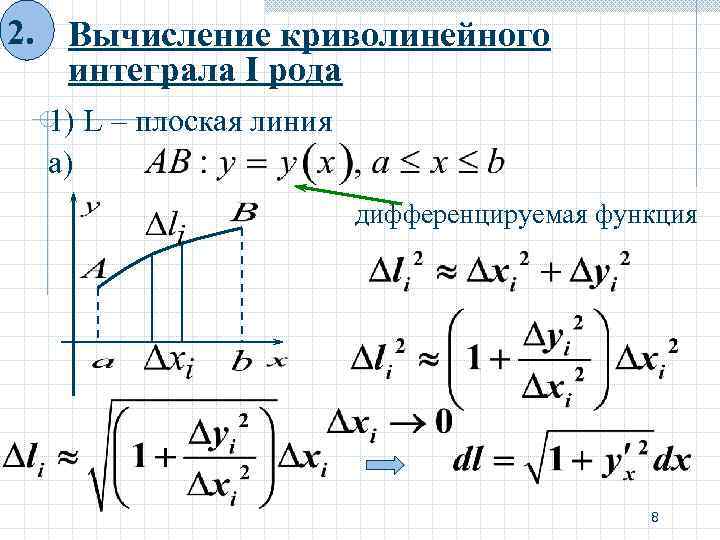2. Вычисление криволинейного интеграла I рода 1) L – плоская линия а) дифференцируемая функция 8

Правило Для вычисления криволинейного интеграла первого рода по плоской кривой необходимо произвести следующие замены: и вычислить определенный интеграл по x. 9

б) - непрерывны на и Тогда 10

Выберем направление отсчета для l так, чтобы возрастанию t соответствовало возрастание длины дуги l. Тогда 11

в) пространственная кривая 12

Полярная система координат 13

Пример Найти массу полуокружности, заданную уравнениями Решение 14

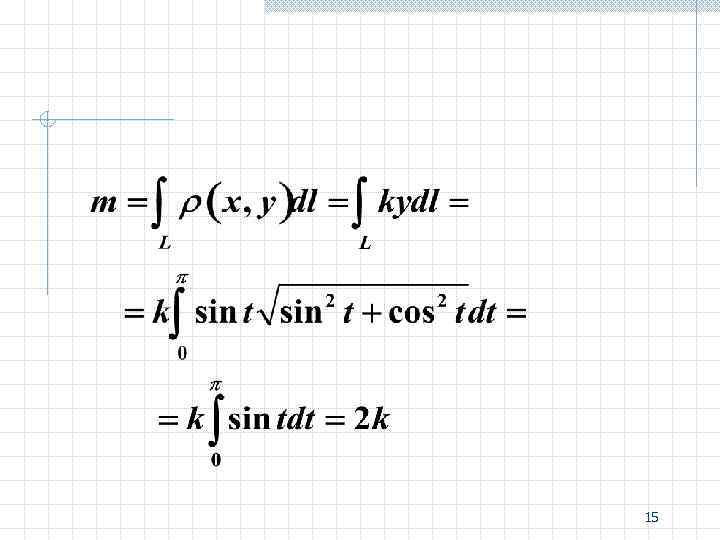15

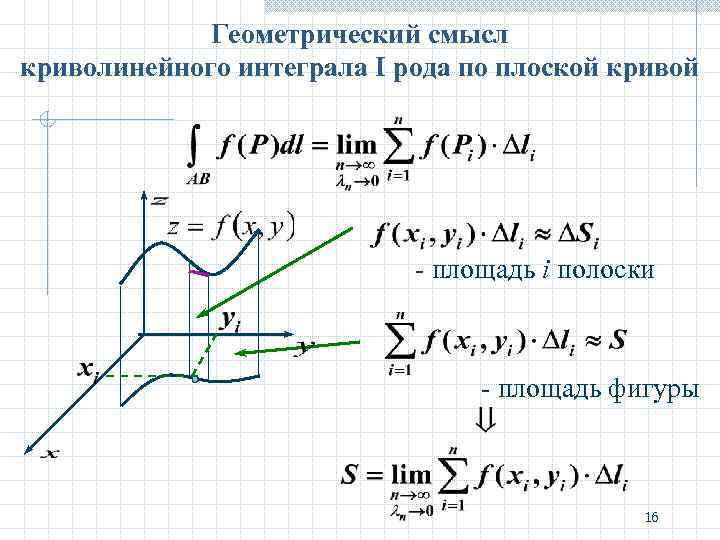Геометрический смысл криволинейного интеграла I рода по плоской кривой - площадь i полоски - площадь фигуры 16

Вывод Если L – плоская кривая, то криволинейный интеграл первого рода численно равен площади боковой поверхности цилиндра с основанием L, образующими, параллельными оси Oz, сверху срезанного графиком подынтегральной функции. 17

Примеры параметризации кривых 1. x - параметр 18

2. Линия пересечения поверхностей Уравнение окружности в параметрическом виде 19

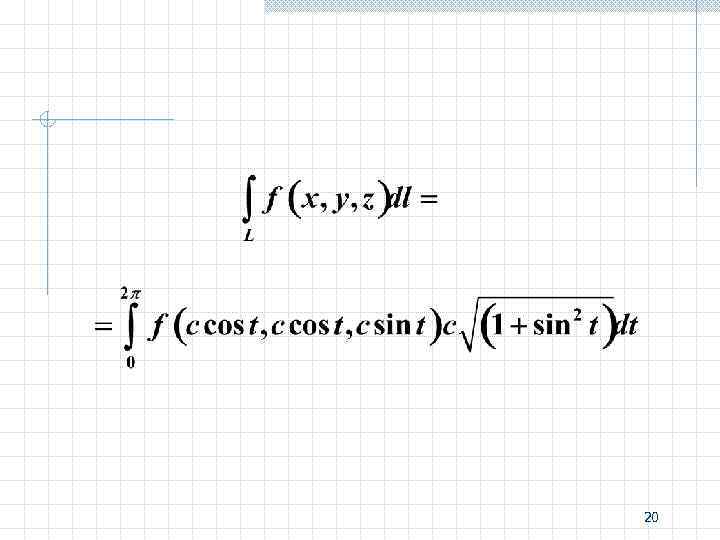20

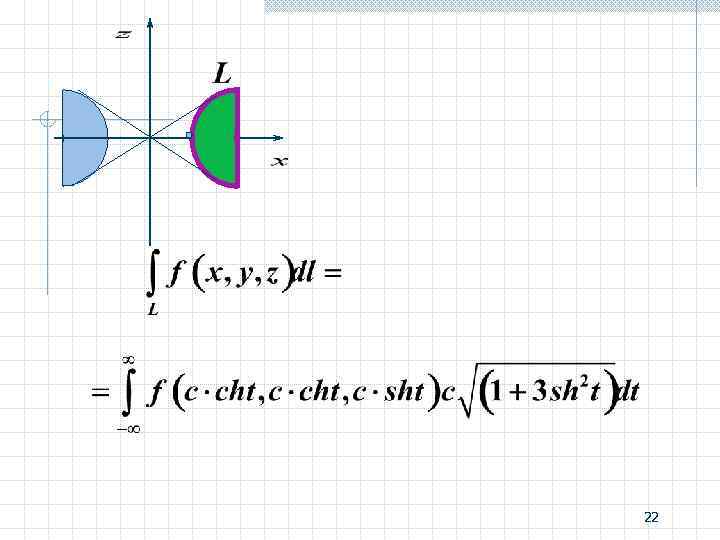
3. - гиперболоид - плоскость Линия пересечения поверхностей - гипербола Параметрические уравнения гиперболы 21

22