Лекция 6_Волновые свойства частиц.ppt
- Количество слайдов: 13

Лекция 6. Гипотеза де- Бройля. Волновые свойства вещества В 1924 году Луи-де-Бройль выдвинул гипотезу о том, что корпускулярно-волновой дуализм не является особенностью одних только оптических явлений, но имеет универсальное значение: Любые частицы вещества наряду с корпускулярными свойствами имеют также и волновые. Т. е. если ЭМВ с частотой и волновым вектором соответствует фотон с соответствующими энергией и импульсом: то и микрочастице (электрону) должна соотв. волна с частотой w и волновым вектором k, удовлетворяющая тем же соотношениям. По идее де-Бройля, движение электрона или какой-либо другой частицы связано с волновым процессом, длина волны: а частота:
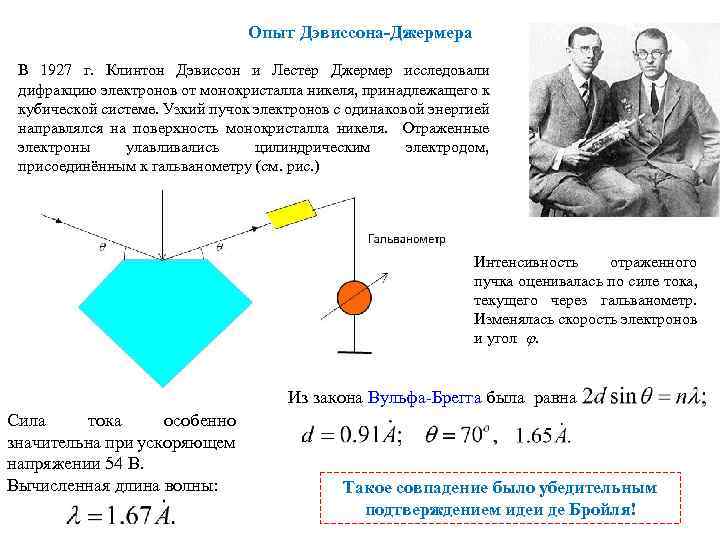
Опыт Дэвиссона-Джермера В 1927 г. Клинтон Дэвиссон и Лестер Джермер исследовали дифракцию электронов от монокристалла никеля, принадлежащего к кубической системе. Узкий пучок электронов с одинаковой энергией направлялся на поверхность монокристалла никеля. Отраженные электроны улавливались цилиндрическим электродом, присоединённым к гальванометру (см. рис. ) Интенсивность отраженного пучка оценивалась по силе тока, текущего через гальванометр. Изменялась скорость электронов и угол . Из закона Вульфа-Брегга была равна Сила тока особенно значительна при ускоряющем напряжении 54 В. Вычисленная длина волны: Такое совпадение было убедительным подтверждением идеи де Бройля!
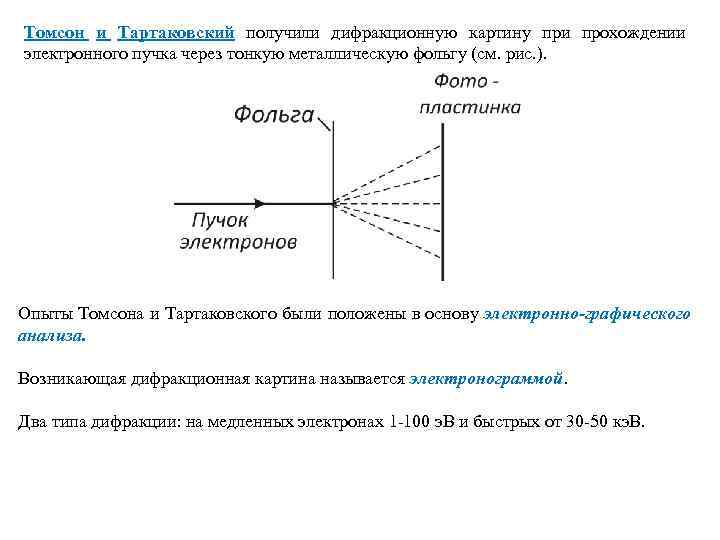
Томсон и Тартаковский получили дифракционную картину при прохождении электронного пучка через тонкую металлическую фольгу (см. рис. ). Опыты Томсона и Тартаковского были положены в основу электронно-графического анализа. Возникающая дифракционная картина называется электронограммой. Два типа дифракции: на медленных электронах 1 -100 э. В и быстрых от 30 -50 кэ. В.

Волна де Бройля и её свойства Равномерно и прямолинейно движущемуся потоку электронов с одинаковой энергией соответствует плоская волна В квантовой механике такую волну, импульс частиц которой точно задан, называют волной де Бройля. Ее физическую природу интерпретируют по Борну, как волну вероятности. Фазовая скорость дебройлевской волны: Т. о. фазовая скорость волны де Бройля больше скорости света в вакууме Электронные волны должны претерпевать большую дисперсию

Групповая скорость волны де Бройля: Групповая скорость волны де Бройля совпадает с фазовой Дисперсия волны де Бройля отсюда Из волн де Бройля нельзя составить волновой пакет. Он расплывается за время

Волновая функция и ее физический смысл Вероятность d. W обнаружить микрочастицу пропорциональна объему пространства d. V, который она занимает : d. W d. V В качестве коэф. пропорц-сти введем функцию : Т. о. состояние физической системы в квантовой механике описывается волновой функцией где xi – координаты микрочастицы Величина имеет смысл плотности вероятности

Если сложная система описывается n- координатами, то d. W- вероятность того, что значение координаты лежит в интервале от до ---------------------координаты лежит в интервале от до Для волны де Бройля имеем: т. е. плотность вероятности найти частицы равномерного потока постоянна во всем пространстве.

Условие нормировки волновой функции Вероятность того, что значения координат системы заключены в бесконечном объеме пространства, следует из определения волновой функции Это условие называют условием нормировки волновой функции. Оно служит для определения постоянного множителя, входящего в волновую функцию. PS. Нормировка не всегда возможна. Например, нельзя нормировать волну де Бройля.

СВОЙСТВА ВОЛНОВОЙ ФУНКЦИИ 1. Конечность. Ни при каких значениях координат она не должна обращаться в бесконечность. 2. Непрерывность. Волновая функция не должна иметь точек, в которых она терпит разрыв. 3. Однозначность. Каждому набору значений аргументов должно соответствовать одно определенное значение волновой функции. Перечисленные свойства необходимы для определения возможных значений физических величин, которые входят в волновую функцию в виде параметров.

Принцип неопределённостей Гейзенберга-Бора Двойственная природа «волна-частица» приводит к вопросу о границе применимости понятий классической механики. Рассмотрим вопрос о невозможности для микрочастицы одновременного определения ее координаты и импульса. Ранее в оптике говорилось, что пространственная ограниченность ∆x цуга волн связана с его принципиальной немонохроматичностью, т. е. неизбежно у такого цуга есть интервал ∆w возможных частот или интервал ∆k волновых чисел монохроматических волн, составляющих этот цуг. Было показано, что между этими интервалами существует связь: Это справедливо для любых волновых процессов В квантовомеханических системах микрочастица не может иметь одновременно точные значения координаты х и соответствующие этой координате составляющую импульса Рх.

Для волны де-Бройля частицы, движущиеся вдоль оси х с импульсом с учетом имеем Это соотношение Гейзенберга-Бора или принцип неопределенностей, который говорит о том, что понятие положения частицы в пространстве и её траектории из классической механики оказывается приближенными и не применимы к движению микрочастиц.

ПРИМЕР. Пусть частица летит на щель. 1. До щели: Координата х в левом полупространстве неопределена. 2. После щели: из-за дифракции она будет в пределах угла 2φ, где φ – угол первого дифракционного минимума, т. е. По закону дифракции т. е. :

Таким образом, ПРИМЕР подтверждает, что произведение неопределенности значений двух сопряженных переменных не может быть по порядку величины меньше ħ. Энергия и время являются также сопряженными величинами. Определение энергии с точностью ΔE должно занять интервал времени Δt, равный
Лекция 6_Волновые свойства частиц.ppt