Лекция 6, 7 1. 2. 3. 4. 5. Понятие «информация» Введение в теорию информации Понятие «энтропии» Понятие «количество информации» Основные результаты теории информации
Понятие «информация» Знания, сведения, сообщения, известия и т. д. Отражения реального мира в различной форме Как только состояние одного объекта приходит в соответствие с состоянием другого объекта. Соответствие устанавливается в результате физического взаимодействия между объектами, причём чаще всего посредством взаимодействия с одним или несколькими промежуточными объектами.
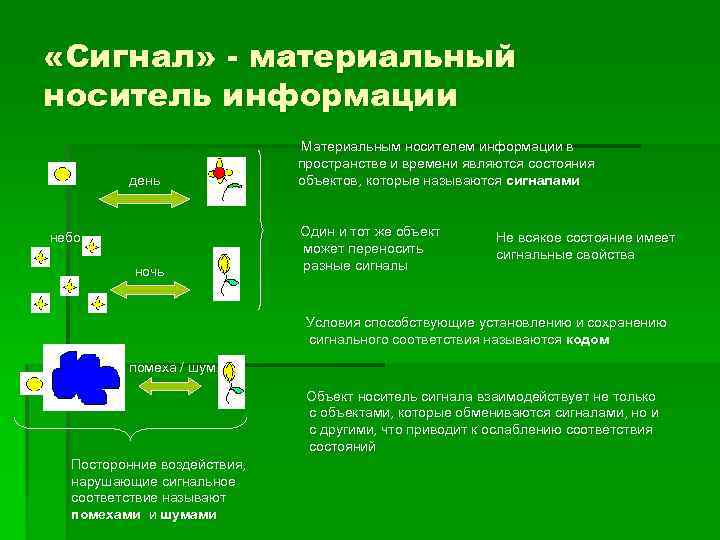«Сигнал» - материальный носитель информации день небо ночь Материальным носителем информации в пространстве и времени являются состояния объектов, которые называются сигналами Один и тот же объект может переносить разные сигналы Не всякое состояние имеет сигнальные свойства Условия способствующие установлению и сохранению сигнального соответствия называются кодом помеха / шум Объект носитель сигнала взаимодействует не только с объектами, которые обмениваются сигналами, но и с другими, что приводит к ослаблению соответствия состояний Посторонние воздействия, нарушающие сигнальное соответствие называют помехами и шумами
Объекты достаточно устойчивы во времени и к изменению положения объекта в пространстве Статические сигналы – стабильные состояния объектов § § Книга Фотография Запись в памяти ЭВМ Наскальный рисунок Динамические сигналы – динамическое состояние силовых полей § Звук § Радио сигналы § Световые сигналы
Непредсказуемость – основное свойств осигналов Пусть X(t) функциональная зависимость состояния объекта от времени Реализация x 1(t) x 2(t) x 3(t) x 4(t) X 5(t) ансамбль Таким образом x(t) приобретает сигнальные свойства если
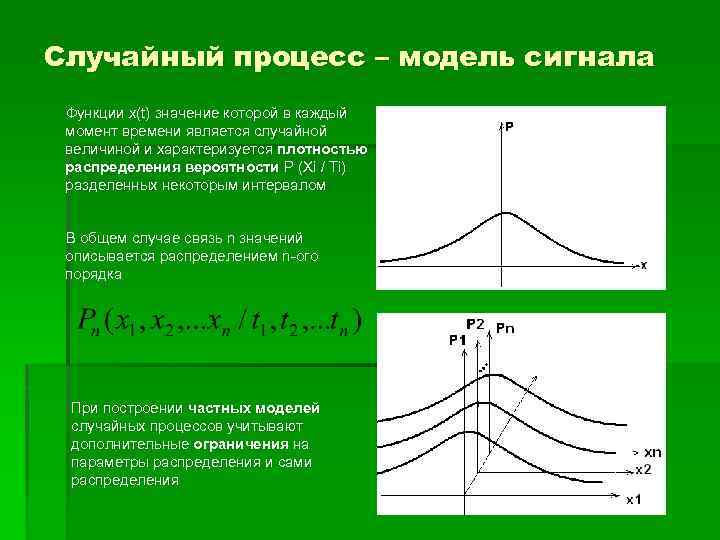Случайный процесс – модель сигнала Функции x(t) значение которой в каждый момент времени является случайной величиной и характеризуется плотностью распределения вероятности P (Xi / Ti) разделенных некоторым интервалом В общем случае связь n значений описывается распределением n-ого порядка При построении частных моделей случайных процессов учитывают дополнительные ограничения на параметры распределения и сами распределения
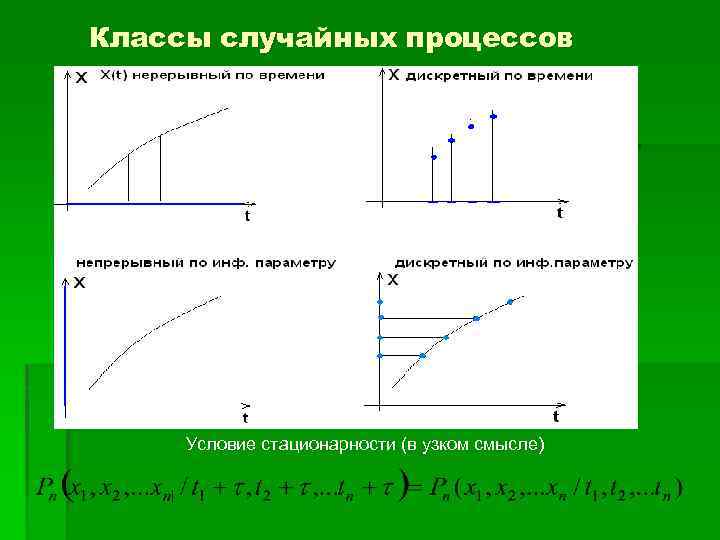Классы случайных процессов Условие стационарности (в узком смысле)
Модели реализаций непрерывных сигналов Модулированные сигналы переносят полезную информацию каким-нибудь одним параметром ограниченной полосой частот. Фурье- Процесс Сигналы с гармонического колебания (несущего колебания). изменения параметра называется модуляцией, а выделение этого изменения реобразование Хa временной реализации хф сигнала в чистом виде - демодуляцией. Пусть параметры с индексом 0 являются называется Сигналы с ограниченной энергией: ее постоянными, тогда : спектром: Периодические сигналы: Гармонические (синусоидальные) о Сигналы из множества длительности. сигналах ограниченной Интервал Т называется сигналы сигнала x(t), если: длительностью Sτ={x: x(t)=x(t+τ); -∞
Принцип частотно-временной неопределённости но
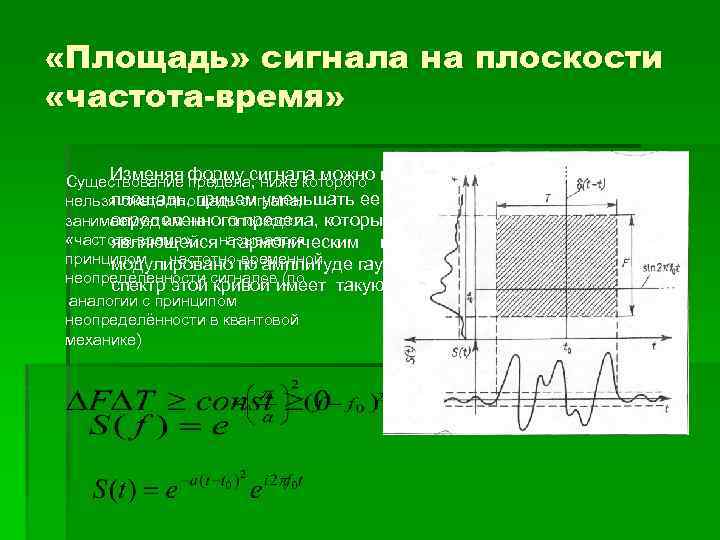«Площадь» сигнала на плоскости «частота-время» Изменяя предела, ниже которого Существование форму сигнала можно изменять и занимаемую им площадь, причем уменьшать ее можно только до нельзя сжать площадь сигнала, занимаемую им на плоскости который достигается на кривой определенного предела, «частота-время» , называется являющейся гармоническим колебанием, которое принципом частотно-временной модулировано по амплитуде гауссовым импульсом. При этом неопределенности сигналовимеет такую же форму: спектр этой кривой (по аналогии с принципом неопределённости в квантовой механике)
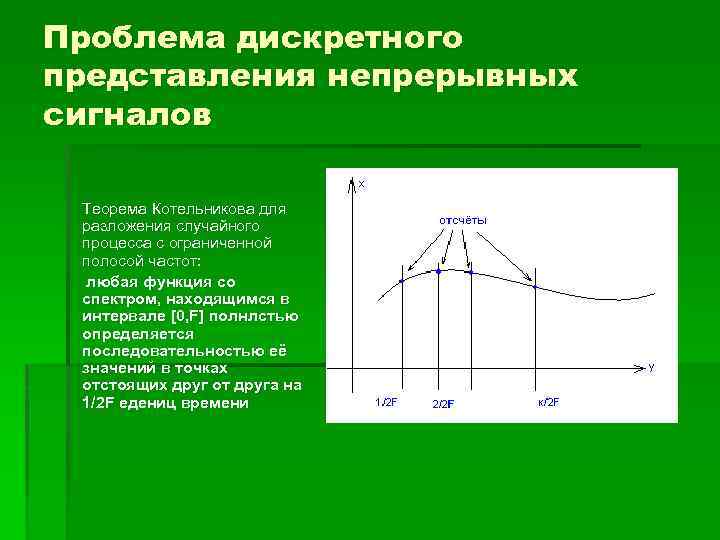Проблема дискретного представления непрерывных сигналов Теорема Котельникова для разложения случайного процесса с ограниченной полосой частот: любая функция со спектром, находящимся в интервале [0, F] полнлстью определяется последовательностью её значений в точках отстоящих друг от друга на 1/2 F едениц времени
Введение в теорию информации Научная дисциплина, которая специально рассматривает сигнальную специфику случайных процессов – теория информации
Понятие «энтропии»
Понятие «энтропии» Количественной мерой неопределенности случайного объекта А с конечным множеством возможных состояний А 1, А 2, …Аn с соответствующими вероятностями p 1, p 2, … pn принимают H(A) = H({pi)} , = -Σpi log pi, I = 1, 2, …n, которую называют энтропией случайного объекта А или распределения (pi) Свойство № 1 H(p 1, …, pn) = 0 только в том случае, когда какоенибудь одно из (pi) равно единице (а остальные нули). Это соответствует случаю когда исход опыта может быть предсказан с полной достоверностью, т. е. при отсутствии любой неопределённости. В других случаях энтропия положительна. Свойство № 2 log n = H(p 1, …, pn) достигает наибольшего значения при p 1 = p 2 =…=pn =1/n, т. е. в случае максимальной неопределённости
Дифференциальная энтропия Обобщение энтропии дискретной случайной величины на непрерывную величину можно выполнить следующим образом: Прямая аналогия не приводит к нужному результату. Плотность p(x) является размерной величиной, а логарифм размерной величины не имеет смысла: Однако если умножить p(x) под знаком логарифма на величину ξ, имеющую ту же размерность, что и х, то: Теперь величину ξ можно принять равной некоторой произвольной единице измерения х, что приводит к функционалу: Т. к. Единица измерения произвольна, то это условный, относительный аналог энтропии дискретной величины. Величина h(x) в отличие от H(x) может быть не только положительной. Также h(x) изменяется при нелинейных преобразованиях шкалы, что в дискретном случае не важно.
Понятие «количество информации» Современное толкование процесса получения информации измерение неопределённости в результате приёма сигнала Полезный (оправляемый) сигнал является последовательностью статистически независимых символов{xi} с вероятностями p(xi), i=1, m шума нет Yk = Xk шум есть Yk = Xk Принимаемый сигнал является последовательностью символов yk того же алфавита. Yk = Xi, P( Yk | Xi ) до получения символа H(x) = max Апостериорная энтропия H (x | y ) = Ø H (x | y ) < Ø Количество информации определяет меру снятой неопределенности: числовое значение количество информации о некотором объекте равно разности априорной и апостериорной энтропии этого объекта, т. е. I (X , Y ) = H (X ) – H (X / Y ) или I(X, Y) = H(Y) – H(Y/X)
Свойство симметрии количества информации Отражаемый и отражающий объекты выступают совершенно равноправно Отражение одного объекта другим есть результат взаимодействия, т. е. взаимного, обоюдного изменения состояний НО Одно явление всегда выступает как причина, другой – как следствие , что никак не учитывается при введенном количественном описании информации Количество информации в объекте Х об объекте Y равно количеству информации в объекте Y об объекте Х. Таким образом количество информации, является не характеристикой одного из объектов, а характеристикой их связи.
Единицы измерения количества информации и энтропии, их безразмерность, одинаковость единиц Из определений I и H следует Из линейности их связи следует их безразмерность одинаковость единиц Для определенности рассмотрим энтропию дискретного случая Для однозначного определения еденицы измерения энтропии необходимо конкретизировать число m состояний объекта и оснований логарифма Пусть Наименьшее число возможных состоянии, при котором объект ещё остаётся случайным, m=2 соответственно в качестве логарифма возьмём также 2 Следовательно единицей неопределенности служит энтропия объекта с двумя равновероятными состояниями. Она получила название «БИТ»
Избыточность Основные характеристики сигнала
Скорость передачи информации Где указанные энтропии исчисляются в единицу времени Темп обычной речи имеет скорость порядка 20 бит/с, муравьи обмениваются информацией со скоростью 1/10 бит/с Скорость передачи информации по каналу связи зависит от энергии сигнала, числа символов в алфавите избыточности, полосы частот, способа кодирования/декодирования Существует предел, выше которого увеличение скорости невозможно, это пропускная способность канала: Где Ra- скорость передачи информации при условиях а, {a}-множество условий подлежащих перебору Каналы первого рода, для которых указанный предел бесконечен Каналы второго рода, имеющие конечную пропускную способность даже при бесконечной мощности передатчика, этот предел и называют мощностью передатчика Пропускные способности зрительного, слухового и тактильного каналов связи человека имеют порядок 50 бит/с. Если включить в канал исполнительные органы человека, то пропускная способность близка к 10 бит/с
Основные результаты теории информации Основными результатами теории информации являются теоремы о существовании которые носят асимптотический характер, т. е. не являются конструктивными Однако уже само знание потенциальных возможностей имеет огромное значение: сравнение характеристик реальных систем с теоретическими пределами позволяет судить о достигнутом уровне и о целесообразности дальнейших затрат на его повышение Эвристическое значение основных понятий теории информации привело к обсуждению новых понятий, к более глубокому пониманию закономерностей природы и к тому, что понятие информации вошло в число философских категорий Конкретные пркланые методы и результаты теории информации позволяют провести ряд количественных исследований информационных потоков в изучаемой или проектируемой системе Системный анализ по определению нацелен на исследование ресурсов, которые потребуются для решения анализируемой проблемы. При этом, если энергетические и вещественные потоки «питают» систему, то потоки информации организуют её функционирование, управляют ею. Винер Н. подчеркивал, что общество простирается, до тех пределов, до каких распространяется информация.
Техническое выполнение презентации: Студент группы 41 -Р Змеёв. А. А. Руководители: д. т. н. , проф. Колоколов Ю. В. , к. т. н. Моновская А. В. Проект «Курс лекций «ИСС» выполнен на кафедре ПТЭи. ВС, Орел. ГТУ, 2006 г.