Лекция 5 Второе начало термодинамики Вопросы к

Лекция 5 Второе начало термодинамики

Вопросы к зачёту 13. Определение второго начала термодинамики. 14. Понятие замкнутой системы. 15. Понятие деградации энергии. Примеры. 16. Принцип двойственности систем. 17. Определение энтропии системы. Формула Больцмана. 18. Свойства замкнутой системы.

Вопросы к зачёту • 19. Открытые системы и их свойства. • 20. Понятие диссипативных структур. Примеры. • 21. Понятие самоорганизации. Примеры. • 22. Как «работают» ячейки Бенара. • 23. Суть синергетического подхода.

Первое начало термодинамики или закон сохранения энергии Q = U + A

Формулировка второго начала термодинамики • Тепло само собой всегда переходит от более нагретого тела к более холодному Или невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.

Замкнутая система Система не обменивающаяся с внешней средой • ни энергией, • ни веществом, • ни информацией.

Формулировка второго начала термодинамики • Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая невозможность перехода всей внутренней энергии системы в полезную работу. • Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на осно ве обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Формулировка второго начала термодинамики • Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса). • Постулат Томсона: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Необратимые процессы • Необратимым называется процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы. Примеры необратимых процессов: диффузия, термодиффузия, теплопроводность, и др.

Деградация энергии • “Высококачественная” световая энергия превращается в энергию химических связей тканей растений, которая затем после гибели растения деградирует в тепловую энергию в процессе гниения. • Деградация энергии – переход от высокоупорядоченной энергии к энергии хаотического движения (т. е. тепловой энергии)

Энтропия Энтропи я (от греч. ἐντροπία — поворот, превращение) — мера беспорядка системы или мера хаотической составляющей любой системы Рудольф Клаузиус Энтропия впервые введена Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Она является функцией состояния и остаётся постоянной в обратимых процессах. В необратимых процессах энтропия увеличивается.

Принцип двойственности систем • Все системы состоят из двух составляющих: хаотической и упорядоченной. Соотношение этих составляющих меняется при всех изменениях системы.

Энтропи я – мера деградации энергии, мера неупорядоченности, неопределённости, нестабильности.

Свойства замкнутой системы • Энергия замкнутой системы остается постоянной. • Энтропия замкнутой системы возрастает

Формула Больцмана S = k ln. W Людвиг Больцман

Демон Максвелла • Демон Максвелла — мысленный эксперимент 1867 года, а также его главный персонаж — гипотетическое разумное существо микроскопического размера, придуманное Джеймсом Максвеллом с целью проиллюстрировать кажущийся парадокс Второго начала термодинамики. Джеймс Максвелл

Суть парадокса • Мысленный эксперимент состоит в следующем: предположим, сосуд с газом разделён непроницаемой перегородкой на две части: правую и левую. В перегородке отверстие с устройством (так называемый демон Максвелла), которое позволя ет пролетать быстрым (горячим) молекулам газа только из левой части сосуда в правую, а медлен- ным (холодным) молекулам — только из правой части сосуда в ле- вую. Тогда, через большой проме жуток времени, горячие молекулы окажутся в правом сосуде, а холод ные — в левом.

Суть парадокса • Таким образом, получается, что демон Максвелла позволяет нагреть правую часть сосуда и охладить левую без дополнительного подвода энергии к системе. Энтропия для системы, состоящей из правой и левой части сосуда, в начальном состоянии больше, чем в конечном, что противоречит термодинамическому принципу неубывания энтропии в замкнутых системах

Демон Максвелла и информация В информатике используется формула Хартли: x=log 2 N. Получена она в 1928 г. американским инженером Р. Хартли. Процесс получения информации он формулировал примерно так: если в заданном множестве, содержащем N равнозначных элементов, выделен некоторый элемент x, о котором известно лишь, что он принадлежит этому множеству, то, чтобы найти x, необходимо получить количество информации, равное log 2 N.

Наименьшее количество информации 1 бит – соответствует выбору одного из двух значений одной цифры при двоичной записи числа (0 или 1). Т. о. получаем из формулы 1=а. Ln 2 и тогда а= 1/Ln 2 Две цифры – два бита и т. д. I цифр – соответствует количеству информации в битах, равному I.

Лекция 6 Открытые системы

• Открытые системы – системы, обменивающиеся с окружающей средой веществом, энергией и информацией. • Энтропия открытой системы может как увеличиваться (в случае регресса и увеличения хаоса), так и уменьшаться (в случае развития и упорядочения).

• Автотрофы (др. -греч. αὐτός — сам и τροφή — пища) — живые организмы, синтезирующие органические соединения из неорганических. • Автотрофы составляют первый ярус в пищевой пирамиде (первые звенья пищевых цепей). Именно они являются первичными продуцентами органического вещества в биосфере, обеспечивая пищей гетеротрофов. Следует отметить, что иногда резкой границы между автотрофами и гетеротрофами провести не удается. Например, одноклеточ- ная эвглена на свету является автотрофом, а в темноте — гетеротрофом.

Диссипативные структуры • Диссипативная система (или диссипативная структура, от лат. dissipatio — «рассеиваю, разрушаю» ) — это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне. Диссипативная система иногда называется ещё стационарной открытой системой или неравновесной открытой системой.

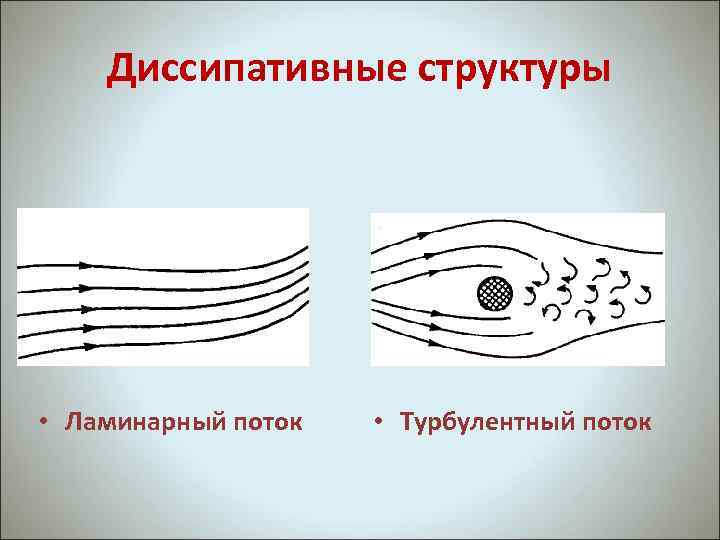Диссипативные структуры • Ламинарный поток • Турбулентный поток

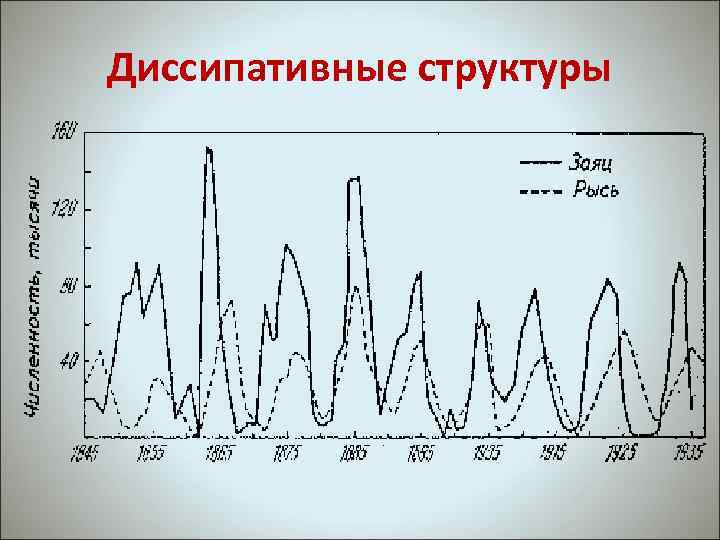
Диссипативные структуры • Диссипативные структуры в экологии связаны в первую очередь с системами "хищник - жертва" или "паразит - хозяин" и представляют собой циклические колебания (временная упорядочен ность), которые исследовались Лоткой (1926) и Вольтеррой (1930). Экспериментально такие колебания впервые наблюдались в Северной Америке для популяций зайцев и рысей на основании данных о числе заготовленных шкурок

Диссипативные структуры

Ячейки Бенара

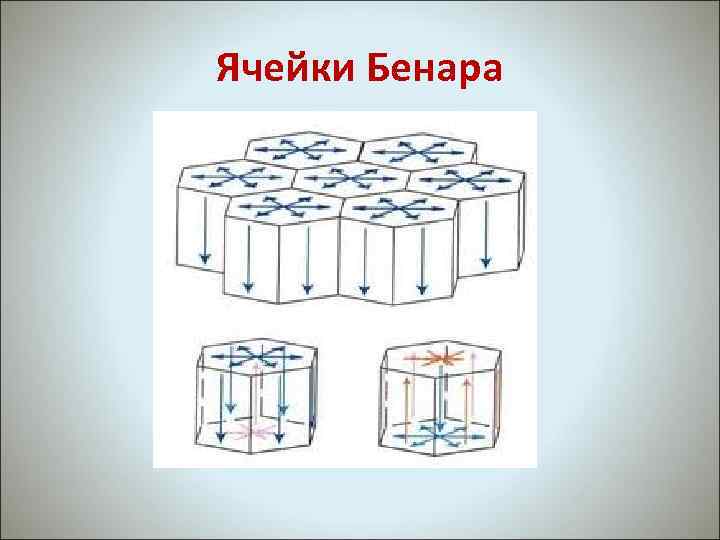Ячейки Бенара

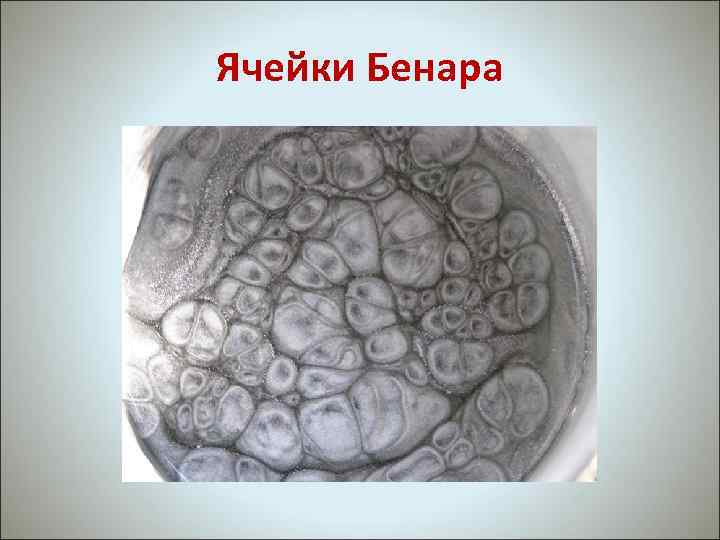Ячейки Бенара

Ячейки Бенара

Ячейки Бенара

Реакция Белоусова Жаботинского

Необходимые свойства самоорганизующихся систем • Система должна быть открытой; • Наличие управляющих параметров; • Наличие внутрисистемных связей.

Схема процесса самоорганизации • внешнее воздействие на систему; • изменение управляющего параметра; • изменение эффективности прежних или образование новых внутрисистемных связей; • образование диссипативных структур, усложнение системы.

Теория Дарвина и самоорганизация или от простого к сложному

Дарвин против Больцмана? Больцман против космоса?

Синергетика • Синергетический подход означает эквивалентность рассмотрения процессов в различных открытых системах, из которых состоит наш мир и проявляющихся как в живой так и неживой природе, так и в общественных, психологических и социальных системах.

Хаос и порядок Порядок из хаоса или хаос из порядка