 Лекция № 5 Тема № 2: ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ Занятие 2. 3. Элементы теории множеств: декартово произведение множеств и бинарные отношения
Лекция № 5 Тема № 2: ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ Занятие 2. 3. Элементы теории множеств: декартово произведение множеств и бинарные отношения
 Учебные вопросы: 1. 2. 3. 4. Основные равносильности теории множеств. Декартово произведение множеств. Отношения и свойства бинарных отношений. О парадоксах интуитивной теории множеств.
Учебные вопросы: 1. 2. 3. 4. Основные равносильности теории множеств. Декартово произведение множеств. Отношения и свойства бинарных отношений. О парадоксах интуитивной теории множеств.
 1. Равносильные (тождественные) преобразования Пример: Пусть дано множество: Зададимся вопросом: "Нельзя ли упростить правую часть приведенного равенства? ".
1. Равносильные (тождественные) преобразования Пример: Пусть дано множество: Зададимся вопросом: "Нельзя ли упростить правую часть приведенного равенства? ".
 На основании закона Де Моргана имеем Снимаем двойное дополнение . Применяем дистрибутивность пересечения относительно объединения:
На основании закона Де Моргана имеем Снимаем двойное дополнение . Применяем дистрибутивность пересечения относительно объединения:
 Используем ассоциативность пересечения: Применяем закон пустого множества: . Еще раз применяем закон пустого множества: И еще один раз:
Используем ассоциативность пересечения: Применяем закон пустого множества: . Еще раз применяем закон пустого множества: И еще один раз:
 Используя коммутативность и ассоциативность пересечения получаем: На основании дистрибутивности пересечения относительно объединения, имеем: . . Используя законы идемпотентности пересечения, получим:
Используя коммутативность и ассоциативность пересечения получаем: На основании дистрибутивности пересечения относительно объединения, имеем: . . Используя законы идемпотентности пересечения, получим:
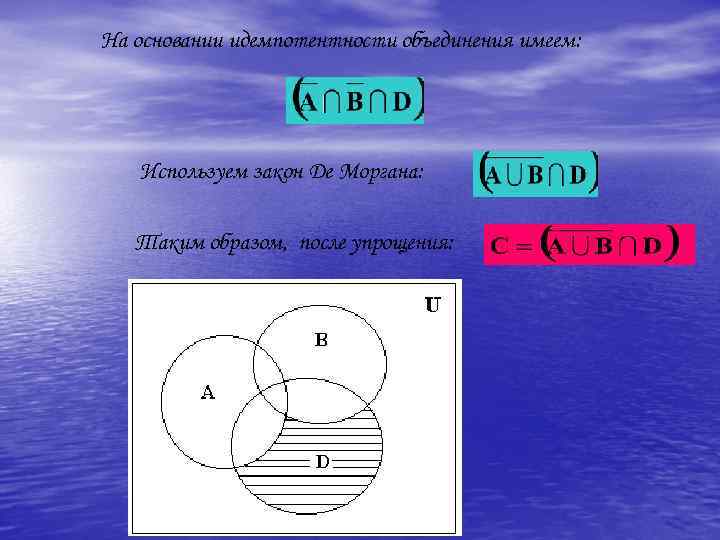 На основании идемпотентности объединения имеем: Используем закон Де Моргана: Таким образом, после упрощения:
На основании идемпотентности объединения имеем: Используем закон Де Моргана: Таким образом, после упрощения:
 2. Декартово произведение множеств Пусть даны два множества: X = {x 1, x 2, x 3, … , xi, … xn, … } и Y = {y 1, y 2, y 3, … , yj, … ym, …}. Декартовым произведением множеств X и Y называют множество Z={
2. Декартово произведение множеств Пусть даны два множества: X = {x 1, x 2, x 3, … , xi, … xn, … } и Y = {y 1, y 2, y 3, … , yj, … ym, …}. Декартовым произведением множеств X и Y называют множество Z={
 Если все множества, участвующие в декартовом произведении, равны, то есть по существу представляют собой одно множество: X 1 = X 2 = X 3 = … = Xn = X. n-тая декартова степень множества X обозначается Xn. В таком случае можно говорить о декартовом квадрате, декартовом кубе множества X и т. п. Интуитивно должно быть ясно, что декартово произведения конечного числа счетных множеств счетно, а декартово произведение конечного числа несчетных множеств несчетно. n-арным (или n-местным) отношением R(X 1, X 2, X 3, … , Xn) называется любое подмножество декартового произведения n множеств X 1, X 2, X 3, … , Xn.
Если все множества, участвующие в декартовом произведении, равны, то есть по существу представляют собой одно множество: X 1 = X 2 = X 3 = … = Xn = X. n-тая декартова степень множества X обозначается Xn. В таком случае можно говорить о декартовом квадрате, декартовом кубе множества X и т. п. Интуитивно должно быть ясно, что декартово произведения конечного числа счетных множеств счетно, а декартово произведение конечного числа несчетных множеств несчетно. n-арным (или n-местным) отношением R(X 1, X 2, X 3, … , Xn) называется любое подмножество декартового произведения n множеств X 1, X 2, X 3, … , Xn.
 Отношение представляет собой некоторую "выборку" из декартового произведения. Декартово произведение, подмножеством которого является отношение, задает область определения (или область определенности) отношения. Если n-арное отношение R определено на n-той декартовой степени множества Х, то будем говорить, что оно просто определено на множестве Х, то есть множество Х является областью определенности отношения R.
Отношение представляет собой некоторую "выборку" из декартового произведения. Декартово произведение, подмножеством которого является отношение, задает область определения (или область определенности) отношения. Если n-арное отношение R определено на n-той декартовой степени множества Х, то будем говорить, что оно просто определено на множестве Х, то есть множество Х является областью определенности отношения R.
 3. Отношения и свойства бинарных отношений.
3. Отношения и свойства бинарных отношений.
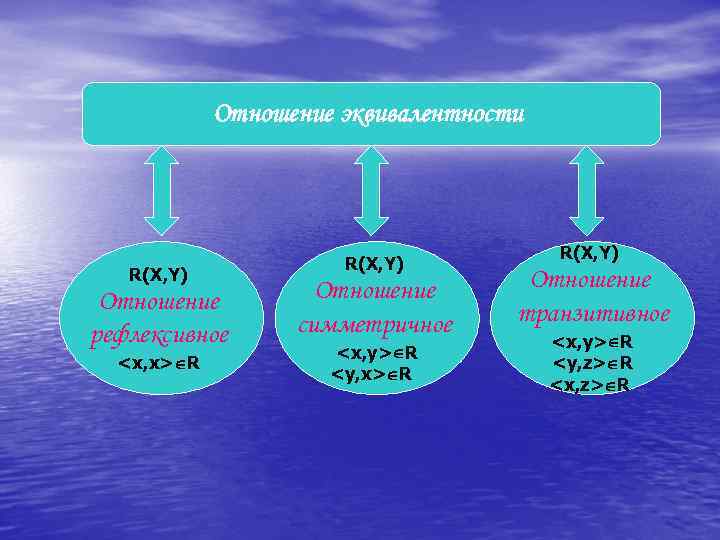 Отношение эквивалентности R(X, Y) Отношение рефлексивное
Отношение эквивалентности R(X, Y) Отношение рефлексивное
 Справедливы следующие свойства разбиения множества на классы эквивалентности: 1. Классы эквивалентности между собой не пересекаются. 2. Объединение всех классов эквивалентности, на которое отношение R разбивает множество X, дает множество X. С другой стороны, любое разбиение множества X на непересекающиеся подмножества задает некоторое отношение эквивалентности R на множестве X.
Справедливы следующие свойства разбиения множества на классы эквивалентности: 1. Классы эквивалентности между собой не пересекаются. 2. Объединение всех классов эквивалентности, на которое отношение R разбивает множество X, дает множество X. С другой стороны, любое разбиение множества X на непересекающиеся подмножества задает некоторое отношение эквивалентности R на множестве X.
 4. О парадоксах интуитивной теории множеств В качестве примера рассмотрим парадокс Рассела. Множество назовем собственным, если оно не является элементом самого себя. Например, множество всех столов само столом не является, то есть не является элементом множества всех столов. Множество назовем несобственным, если оно является элементом самого себя. Например, множество всех идей само является идеей, то есть является элементом множества всех идей. То есть, сами по себе понятия «собственное» и «несобственное» множества имеют «право на существование» . Ясно, что любое множество является либо собственным, либо несобственным.
4. О парадоксах интуитивной теории множеств В качестве примера рассмотрим парадокс Рассела. Множество назовем собственным, если оно не является элементом самого себя. Например, множество всех столов само столом не является, то есть не является элементом множества всех столов. Множество назовем несобственным, если оно является элементом самого себя. Например, множество всех идей само является идеей, то есть является элементом множества всех идей. То есть, сами по себе понятия «собственное» и «несобственное» множества имеют «право на существование» . Ясно, что любое множество является либо собственным, либо несобственным.
 Рассмотрим множество всех собственных множеств Р. Зададимся вопросом: каким является само это множество Р, то есть, собственное оно или несобственное? 1. Пусть Р собственное множество. Тогда, поскольку Р - есть множество всех собственных множеств, должно иметь место: Р Р. Но Р Р говорит о том, что множество Р является элементом самого себя, то есть должно быть признано нами как несобственное множество. Итак: если Р - собственное, то Р - несобственное. 2. Пусть теперь Р - несобственное множество. Это означает, что Р является элементом самого себя, то есть Р Р. Но поскольку Р множество всех собственных множеств, то как элемент этого множества множество Р тоже должно быть признано собственным. Итак: если Р - несобственное, то Р - собственное. В приведенном рассуждении используются лишь начальные понятия теории множеств: понятие множества как некоторой совокупности элементов, понятие элемента множества, понятия «элемент принадлежит множеству» и «элемент не принадлежит множеству» . И больше ничего! Тем не менее, парадокс налицо.
Рассмотрим множество всех собственных множеств Р. Зададимся вопросом: каким является само это множество Р, то есть, собственное оно или несобственное? 1. Пусть Р собственное множество. Тогда, поскольку Р - есть множество всех собственных множеств, должно иметь место: Р Р. Но Р Р говорит о том, что множество Р является элементом самого себя, то есть должно быть признано нами как несобственное множество. Итак: если Р - собственное, то Р - несобственное. 2. Пусть теперь Р - несобственное множество. Это означает, что Р является элементом самого себя, то есть Р Р. Но поскольку Р множество всех собственных множеств, то как элемент этого множества множество Р тоже должно быть признано собственным. Итак: если Р - несобственное, то Р - собственное. В приведенном рассуждении используются лишь начальные понятия теории множеств: понятие множества как некоторой совокупности элементов, понятие элемента множества, понятия «элемент принадлежит множеству» и «элемент не принадлежит множеству» . И больше ничего! Тем не менее, парадокс налицо.
 Литература: 1. Колесников Н. Г. Математические и логические основы информатики. Краснодар издат. Куб. АГУ. 2000 г. 224 с. 2. Калбертсон Дж. Т. Математика и логика цифровых устройств. -М. : Прсвещение, 1965. -267 с. 3. Кук Д. , Бейз Г. Компьютерная математика. – М. : Наука, 1990. 4. Мальцев А. И. Алгебраические системы. – М. : Наука, 1970. 5. Ершов Ю. Л. , Палютин Е. А. Математическая логика. – М. : Наука, 1979. 6. Верещагин Н. К. , Шень А. Начала теории множеств М. МЦНМО, 1999 г. , 127 с.
Литература: 1. Колесников Н. Г. Математические и логические основы информатики. Краснодар издат. Куб. АГУ. 2000 г. 224 с. 2. Калбертсон Дж. Т. Математика и логика цифровых устройств. -М. : Прсвещение, 1965. -267 с. 3. Кук Д. , Бейз Г. Компьютерная математика. – М. : Наука, 1990. 4. Мальцев А. И. Алгебраические системы. – М. : Наука, 1970. 5. Ершов Ю. Л. , Палютин Е. А. Математическая логика. – М. : Наука, 1979. 6. Верещагин Н. К. , Шень А. Начала теории множеств М. МЦНМО, 1999 г. , 127 с.


