 Лекция 5 , т. к. - касательное ускорение точки направлен по касательной к траектории Определим направление и величину второго слагаемого:
Лекция 5 , т. к. - касательное ускорение точки направлен по касательной к траектории Определим направление и величину второго слагаемого:
 Направление - с : Т. к. b О + a 0: Вектора кости, а т. к. нормали. , то и ; 0 ; лежат в соприкасающейся плос, то он направлен по главной
Направление - с : Т. к. b О + a 0: Вектора кости, а т. к. нормали. , то и ; 0 ; лежат в соприкасающейся плос, то он направлен по главной
 Величина b : Из a или . . Из геометрии: ( - кривизна траектории в т. М - радиус кривизны) , следовательно
Величина b : Из a или . . Из геометрии: ( - кривизна траектории в т. М - радиус кривизны) , следовательно
 - нормальное ускорение точки направлен по главной нормали Итак: ; ; Ускорение точки лежит в соприкасающейся плоскости.
- нормальное ускорение точки направлен по главной нормали Итак: ; ; Ускорение точки лежит в соприкасающейся плоскости.
 Частные случаи движения точки Если знаки и совпадают, то такое движение называется ускоренным. -О+ Если знаки ным. - О+ или и - О+ не совпадают, то замедленили - О +
Частные случаи движения точки Если знаки и совпадают, то такое движение называется ускоренным. -О+ Если знаки ным. - О+ или и - О+ не совпадают, то замедленили - О +
 Если , то движение называется равнопеременным: равноускоренным или равнозамедленным. Если , то движение называется равномерным. При прямолинейном движении: , т. к. , сл.
Если , то движение называется равнопеременным: равноускоренным или равнозамедленным. Если , то движение называется равномерным. При прямолинейном движении: , т. к. , сл.
 Перейдем от кинематики точки к кинематике твердого тела. Рассмотрим сначала простейшие движения т. т. : поступательное и вращательное движения.
Перейдем от кинематики точки к кинематике твердого тела. Рассмотрим сначала простейшие движения т. т. : поступательное и вращательное движения.
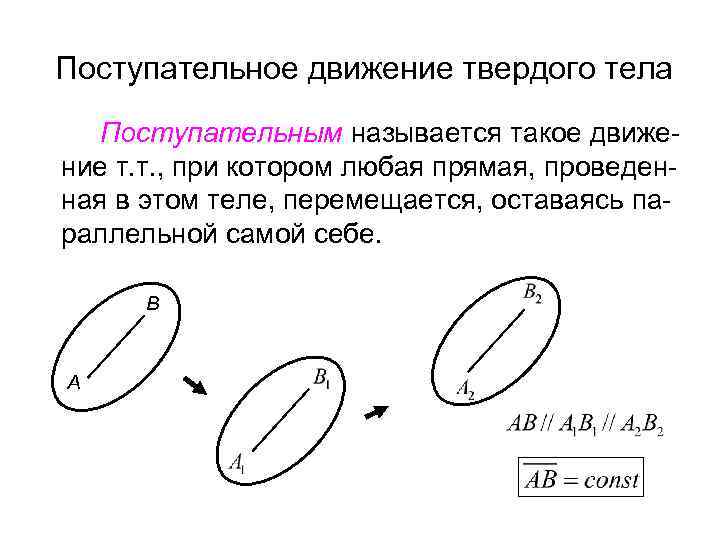 Поступательное движение твердого тела Поступательным называется такое движение т. т. , при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной самой себе. В А
Поступательное движение твердого тела Поступательным называется такое движение т. т. , при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной самой себе. В А
 Теорема: при поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. z В А О x y Т. к. , из уравнения следует, что положение т. В при любом положении тела можно получить, сместив т. А на величину, равную постоянному вектору. Таким образом, траектория т. В одинакова с траекторией т. А, но смещена относительно ее на
Теорема: при поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. z В А О x y Т. к. , из уравнения следует, что положение т. В при любом положении тела можно получить, сместив т. А на величину, равную постоянному вектору. Таким образом, траектория т. В одинакова с траекторией т. А, но смещена относительно ее на
 Продифференцируем уравнение по времени, получим: или ч. т. д. Таким образом, изучение поступательного движения т. т. сводится к изучению движения ка-кой - либо его точки. Обычно в качестве ее рассматривают т. С – центр тяжести тела. - уравнения поступательного движения т. т.
Продифференцируем уравнение по времени, получим: или ч. т. д. Таким образом, изучение поступательного движения т. т. сводится к изучению движения ка-кой - либо его точки. Обычно в качестве ее рассматривают т. С – центр тяжести тела. - уравнения поступательного движения т. т.
 Вращательное движение твердого тела Вращательным называется такое движение т. т. , при котором две точки, принадлежащие телу, остаются во все время движения неподвижными. Прямая, проходящая через эти В две точки, называется осью вращения. Положение тела в любой момент времени однозначно оп. М ределяется взятым с соответ. I ствующим знаком углом по. А II ворота тела.
Вращательное движение твердого тела Вращательным называется такое движение т. т. , при котором две точки, принадлежащие телу, остаются во все время движения неподвижными. Прямая, проходящая через эти В две точки, называется осью вращения. Положение тела в любой момент времени однозначно оп. М ределяется взятым с соответ. I ствующим знаком углом по. А II ворота тела.
 Итак: - уравнение вращательного движения т. т. II I + - средняя угловая скорость тела за II - угловая скорость тела в данный момент времени В технике: - частота вращения
Итак: - уравнение вращательного движения т. т. II I + - средняя угловая скорость тела за II - угловая скорость тела в данный момент времени В технике: - частота вращения
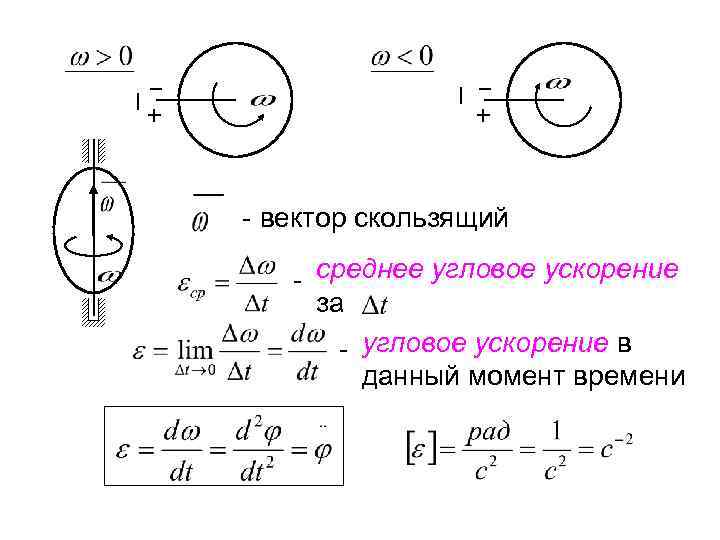 I + - вектор скользящий - среднее угловое ускорение за - угловое ускорение в данный момент времени
I + - вектор скользящий - среднее угловое ускорение за - угловое ускорение в данный момент времени
 I + Если знаки и совпадают, то ускоренное вращение Если нет, то замедленное
I + Если знаки и совпадают, то ускоренное вращение Если нет, то замедленное
 Скорости и ускорения точек вращающегося тела Рассмотрим движение т. М, находящейся на расстоянии от оси вращения Ускоренное вращение: I +
Скорости и ускорения точек вращающегося тела Рассмотрим движение т. М, находящейся на расстоянии от оси вращения Ускоренное вращение: I +
 Итак: Замедленное вращение:
Итак: Замедленное вращение:
 Перейдем к векторам: Докажем, что 1. Вектор пл. 2. 3. Направлен Значит как и - формула Эйлера
Перейдем к векторам: Докажем, что 1. Вектор пл. 2. 3. Направлен Значит как и - формула Эйлера
 Итак:
Итак:


