Лекция 5 Регрессионный анализ Понятие о регрессии

Лекция 5 Регрессионный анализ

Понятие о регрессии l l l l Коэффициент корреляции указывает лишь на степень (тесноту) связи двух переменных величин Коэффициент регрессии позволяет судить о том, как количественно меняется одна величина по мере изменения другой на единицу измерения Так как изменчивых величин две, то регрессия может быть двухсторонней: 1) определение изменения «y» по изменению «х» ; 2) определение изменения «х» по изменению «у» Различают прямолинейную и криволинейную регрессии При прямолинейной регрессии одинаковым приращениям одного признака соответствуют одинаковые приращения другого признака При криволинейной регрессии одинаковым приращениям одного признака соответствуют разные приращения другого признака. Регрессию можно выразить несколькими способами: 1) путем построения эмпирических линий регрессии; 2) путем составления уравнения регрессии и на этой основе построения теоретических линий регрессии; 3) путем вычисления коэффициента регрессии 2

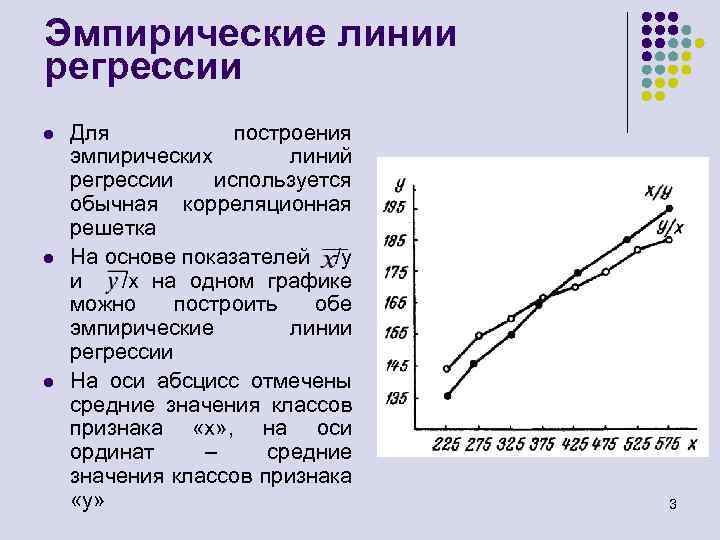Эмпирические линии регрессии l l l Для построения эмпирических линий регрессии используется обычная корреляционная решетка На основе показателей /у и /х на одном графике можно построить обе эмпирические линии регрессии На оси абсцисс отмечены средние значения классов признака «х» , на оси ординат – средние значения классов признака «у» 3

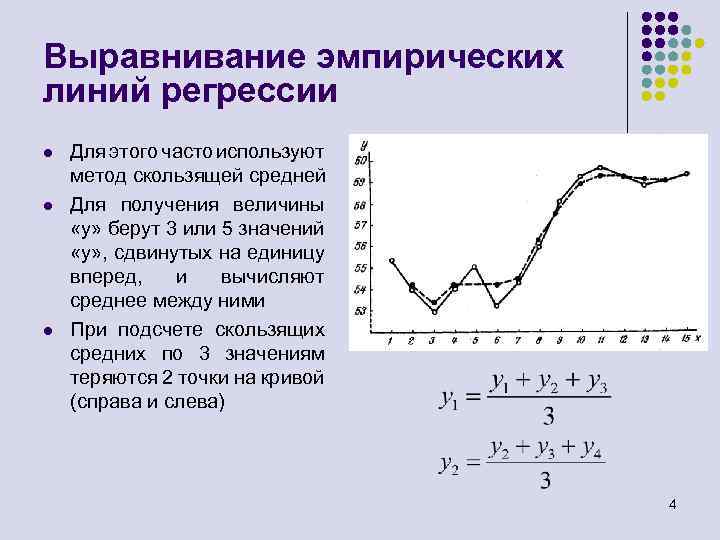Выравнивание эмпирических линий регрессии l l l Для этого часто используют метод скользящей средней Для получения величины «у» берут 3 или 5 значений «у» , сдвинутых на единицу вперед, и вычисляют среднее между ними При подсчете скользящих средних по 3 значениям теряются 2 точки на кривой (справа и слева) 4

Уравнение прямолинейной регрессии l l Показатель «b» является коэффициентом пропорциональности, то есть, величиной указывающей на количественную связь в изменении «у» при изменении «х» Преобразуем это уравнение: Если х=0, то «у» принимает некоторое значение «а» , тогда: (уравнение прямой) Для определения значений «а» и «b» необходимо решить систему двух уравнений: 5

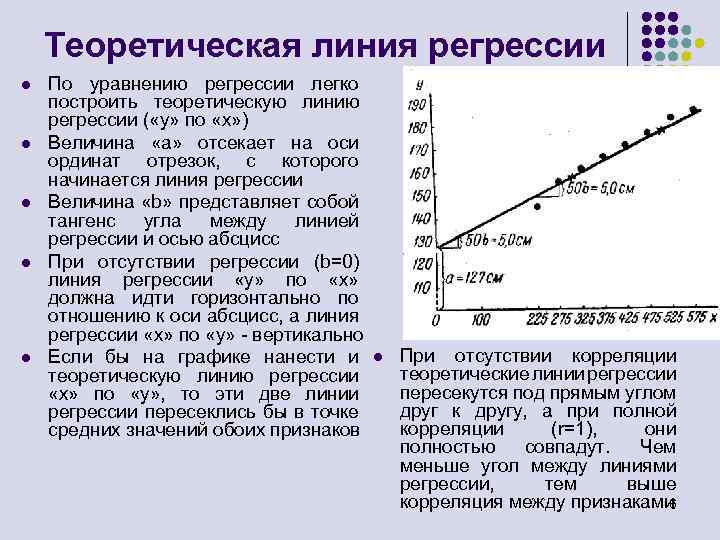Теоретическая линия регрессии l l l По уравнению регрессии легко построить теоретическую линию регрессии ( «у» по «х» ) Величина «а» отсекает на оси ординат отрезок, с которого начинается линия регрессии Величина «b» представляет собой тангенс угла между линией регрессии и осью абсцисс При отсутствии регрессии (b=0) линия регрессии «у» по «х» должна идти горизонтально по отношению к оси абсцисс, а линия регрессии «х» по «у» - вертикально Если бы на графике нанести и теоретическую линию регрессии «х» по «у» , то эти две линии регрессии пересеклись бы в точке средних значений обоих признаков l При отсутствии корреляции теоретические линии регрессии пересекутся под прямым углом друг к другу, а при полной корреляции (r=1), они полностью совпадут. Чем меньше угол между линиями регрессии, тем выше корреляция между признаками 6

Коэффициент регрессии l l Величина «b» представляет собой коэффициент регрессии Коэффициентов регрессии может быть два: 1) bx/y; 2) by/x 7

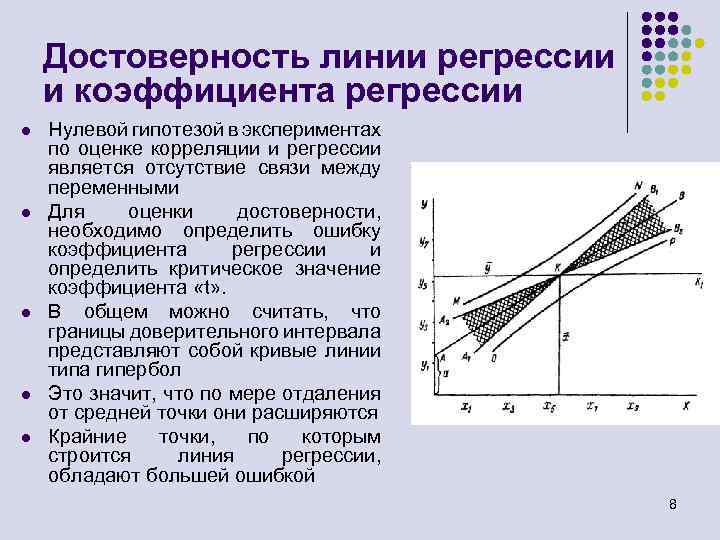Достоверность линии регрессии и коэффициента регрессии l l l Нулевой гипотезой в экспериментах по оценке корреляции и регрессии является отсутствие связи между переменными Для оценки достоверности, необходимо определить ошибку коэффициента регрессии и определить критическое значение коэффициента «t» . В общем можно считать, что границы доверительного интервала представляют собой кривые линии типа гипербол Это значит, что по мере отдаления от средней точки они расширяются Крайние точки, по которым строится линия регрессии, обладают большей ошибкой 8

Достоверность линии регрессии и коэффициента регрессии (df=N-2) 9

Сравнение коэффициентов регрессии (при малых объемах выборок) 10

Связь между регрессией и корреляцией l коэффициент корреляции представляет собой геометрическую из двух коэффициентов регрессии: среднюю l В формулах коэффициентов корреляции и коэффициентов регрессии центральное место занимает сумма произведений отклонений вариант от средних по ряду «х» и по ряду «у» , которая, в сущности, является основным мерилом сопряженной вариации двух признаков, эта сумма произведений носит название – ковариация: 11

Криволинейная регрессия. Параболические кривые второго порядка l Отличается тем, что сначала наблюдается подъем кривой до максимума, а затем её снижение. Выражается уравнением параболы второго порядка: у=а+bx+cx 2 l Чтобы получить значения параметров «а» , «b» и «с» , необходимо составить и решить систему из 3 уравнений: 1) na+(Σxi)b+(Σxi 2)c=Σyi 2) (Σxi)a+(Σxi 2)b+(Σxi 3)c=Σxiyi 3) (Σxi 2)a+(Σxi 3)b+(Σxi 4)c= Σxi 2 yi 12

Криволинейная регрессия. Экспоненциальные кривые l l l Экспоненциальная кривая подымается вверх со все возрастающей скоростью Это выражается уравнением: y=abx Логарифмируя это уравнение, получим: logy=loga+(logb)x, что соответствует уравнению прямой 13