рац. кормл.ppt
- Количество слайдов: 50

ЛЕКЦИЯ 5 РАЗРАБОТКА ЭКОНОМИКОМАТЕМАТИЧЕСКОЙ МОДЕЛИ ОПТИМИЗАЦИИ СУТОЧНОГО КОРМОВОГО РАЦИОНА ЖИВОТНЫХ 1. Постановка задачи 2. Структурная запись экономико-математической модели 3. Подготовка входной информации 4. Построение числовой экономико-математической модели 5. Анализ результатов решения задачи

1. Постановка задачи Характеристика объекта моделирования Скотоводство в хозяйстве является основной отраслью животноводства, на его долю приходилось в 2010 -2014 гг. 23, 9 -41, 4% всей товарной продукции, в том числе на молоко 15, 2 -24, 2%. Хозяйство содержит 1009 голов крупного рогатого скота, в том числе 300 коров. Среднегодовой надой молока на 1 корову составляет 2750 кг или среднесуточная продуктивность 9 кг.

1. Постановка задачи Организация рационального кормления молочного скота должна основываться на знании их потребности в энергии, питательных, биологически активных веществах, необходимых для синтеза молока, сохранения воспроизводительных функций и здоровья животных. В среднем коровы потребляют 2, 8 -3, 2 кг сухого вещества на 100 кг живой массы, 8 -11 МДж обменной энергии на 1 кг сухого вещества.

1. Постановка задачи Молочная продуктивность коров во многом определяется обеспеченностью рациона протеином. Норма переваримого протеина на 1 кормовую единицу составляет в зависимости от суточного удоя 95 -110 г. В рационе должно содержаться оптимальное количество клетчатки - 20 -28% от сухого вещества. Сахаропротеиновое отношение должно находиться в пределах 0, 8 -1, 1, а соотношение крахмала и сахаров 1, 5: 1. Количество жира в рационе должно составлять 60 -65 % от общего их содержания в суточном удое.

1. Постановка задачи В число основных нормируемых макроэлементов входят кальций, фосфор, натрий, хлор, магний, калий, сера, микроэлементов – марганец, йод, кобальт, медь, цинк, бор. Их недостаток может вызвать серьезные нарушения воспроизводительных функций коров. Обеспечение рационов витаминами необходимо для получения высокой продуктивности коров, улучшения воспроизводительных функций, нормализации обмена веществ. Дойные коровы особенно нуждаются в каротине, витаминах D и E.

1. Постановка задачи Полноценное кормление - один из главных факторов обеспечения высокой продуктивности сельскохозяйственных животных. Из одних и тех же кормов можно составить несколько вариантов рациона кормления. Экономикоматематические методы и ЭВМ позволяют выбрать оптимальный, наилучший вариант кормового рациона, сбалансированного по всем элементам питания и имеющего наименьшую стоимость.

1. Постановка задачи Разработаем экономико-математическую модель оптимизации кормового рациона для коровы массой 500 кг и суточным надоем молока 9 кг. Сформулируем цель задачи: исходя из имеющихся в наличии кормов, составить такой суточный рацион кормления коров в стойловый период, который удовлетворил бы потребность животного в питательных веществах, обеспечил плановую продуктивность и был бы самым дешевым.

1. Постановка задачи Основными переменными модели являются количества кормов, которые должны войти в рацион. Основные ограничения отражают условия по балансу элементов питания (кормовых единиц, обменной энергии, сухого вещества, протеина и др. ). Технико-экономические коэффициенты в этих ограничениях означают содержание соответствующих элементов питания в единице корма (в 1 кг). Константы в правой части ограничений (объемы) показывают минимальное количество питательных веществ, которое должно содержаться в рационе. С помощью дополнительных ограничений записывают условия по соотношению отдельных групп кормов в рационе и отдельных видов кормов внутри групп. Критерий оптимальности – минимум стоимости рациона.

2. Структурная запись экономикоматематической модели Экономико-математическую модель в структурном виде можно выразить через следующие условные обозначения: индексы: i - порядковый номер элемента питания корма; j - порядковый номер вида корма в рационе; к - номер группы кормов; множества: I - множество элементов питания животных; J - множество видов кормов; К - множество групп кормов; переменные: хj - искомая переменная, означающая количество j-ro вида корма, включаемого в рацион; х - вспомогательная переменная, обозначающая суммарное количество элементов питания в рационе;

2. Структурная запись экономикоматематической модели коэффициенты: - - минимально возможная доля кормов к - й группы суммарном количестве кормовых единиц; - - максимально возможная доля кормов к - й группы в суммарном количестве кормовых единиц; σjk - возможная доля включения j-ro вида корма в к - ю группу кормов; bi - минимальная потребность животного в i - м элементе питания; aij - содержание i - го элемента питания в j - м виде корма; cj - себестоимость или цена приобретения единицы j-ro вида корма;

2. Структурная запись экономикоматематической модели Структурная запись экономико-математической модели будет иметь следующий вид. Необходимо определить значения переменных xj, при которых целевая функция достигает экстремального значения: При этом должны соблюдаться следующие условия: 1. Рацион должен быть сбалансированным по питательным веществам:

2. Структурная запись экономикоматематической модели 2. Содержание кормов каждой группы (вида) в рационе должно быть ограничено: 3. В отдельных группах кормов содержание некоторых видов кормов может быть ограничено: 4. Условие неотрицательности переменных: xj 0.

3. Подготовка входной информации Входная информация для экономикоматематической модели – это техникоэкономические коэффициенты при переменных, оценки переменных в целевой функции и объёмы ограничений (константы).

3. Подготовка входной информации Для разработки числовой экономико-математической модели задачи по оптимизации рационов кормления животных необходимы следующие данные: • Виды кормов, имеющиеся в хозяйстве; • Суточная потребность животного в питательных веществах. • Содержание питательных веществ в единице массы кормов, имеющихся в хозяйстве. • Стоимость единицы кормов, входящих в состав рациона. • Научные рекомендации по допустимым пределам содержания различных групп кормов и добавок в рационе.

3. Подготовка входной информации В хозяйстве имеются следующие виды кормов: ячмень, отруби, шрот подсолнечный, солома пшеничная, солома ячменная, солома просяная, сено суданковое, сенаж суданковый, силос кукурузный, кормовая свёкла. С помощью справочника «Нормы и рационы кормления с. -х. животных» определим суточную потребность животного в элементах питания и представим в таблице 5. 1.
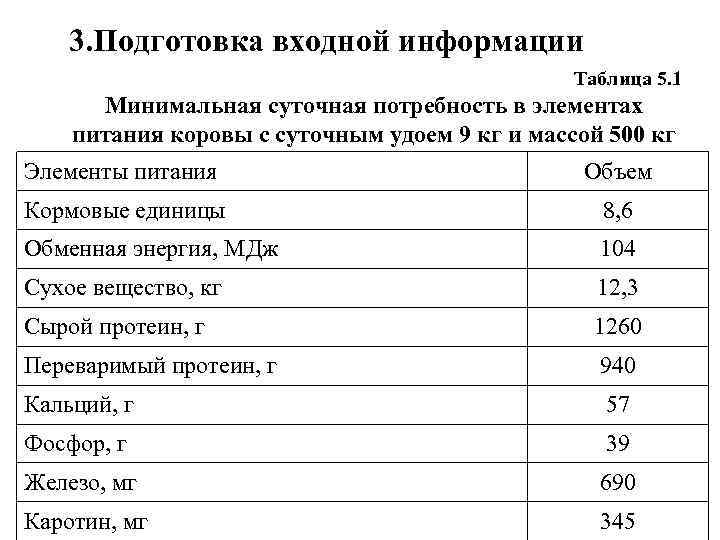
3. Подготовка входной информации Таблица 5. 1 Минимальная суточная потребность в элементах питания коровы с суточным удоем 9 кг и массой 500 кг Элементы питания Объем Кормовые единицы 8, 6 Обменная энергия, МДж 104 Сухое вещество, кг 12, 3 Сырой протеин, г 1260 Переваримый протеин, г 940 Кальций, г 57 Фосфор, г 39 Железо, мг 690 Каротин, мг 345

В этом же справочнике найдём содержание элементов питания в 1 кг корма Таблица 5. 2 Содержание питательных веществ в 1 кг корма Элементы питания Ячмень Отруби пшен. Шрот подсо лнечн ый Солома пшен. Соло- Соло ма ма ячмен. прос. Сено суда нковое Сенаж Силос Кормо кукувая рузный свекла Кормовые единицы 1, 15 0, 75 1, 03 0, 22 0, 34 0, 40 0, 57 0, 35 0, 20 0, 12 Обменная энергия, МДж 10, 5 9, 41 9, 87 4, 91 5, 71 6, 42 7, 9 4, 19 2, 30 1, 65 Сухое вещество, кг 0, 85 0, 9 0, 849 0, 83 0, 845 0, 865 0, 45 0, 25 120 Сырой протеин, г 113 151 429 46 49 57 121 103 25 13 Переваримый протеин, г 85 97 386 9 13 23 74 71 14 9 Кальций, г 2 2, 0 3, 6 3, 3 5, 4 6 10, 9 1, 4 0, 4 Фосфор, г 3, 9 9, 6 12, 2 0, 9 0, 8 1, 0 1, 6 1, 0 0, 4 0, 5 Железо, мг 50 170 332 409 373 790 117 126 61 8, 0 Каротин, мг 0, 5 2, 6 3 5 4 8 15 40 20 0, 1

3. Подготовка входной информации • Стоимость кормов берется на основе фактически сложившейся в хозяйстве себестоимости единицы корма (табл. 5. 3).
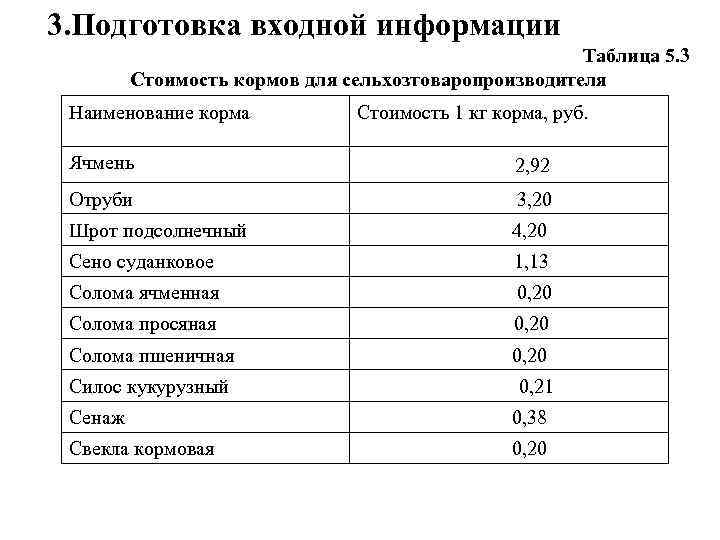
3. Подготовка входной информации Таблица 5. 3 Стоимость кормов для сельхозтоваропроизводителя Наименование корма Стоимость 1 кг корма, руб. Ячмень 2, 92 Отруби 3, 20 Шрот подсолнечный 4, 20 Сено суданковое 1, 13 Солома ячменная 0, 20 Солома просяная 0, 20 Солома пшеничная 0, 20 Силос кукурузный 0, 21 Сенаж 0, 38 Свекла кормовая 0, 20

3. Подготовка входной информации Для жвачных животных существуют определенные пределы насыщения рациона отдельными группами кормов: концентрированные должны составлять 1530% питательности рациона, грубые 2060%, сочные 20 -65%. На их основе рассчитаны нижние и верхние границы содержания концентрированных, грубых и сочных кормов в суточном рационе коровы (табл. 5. 4).
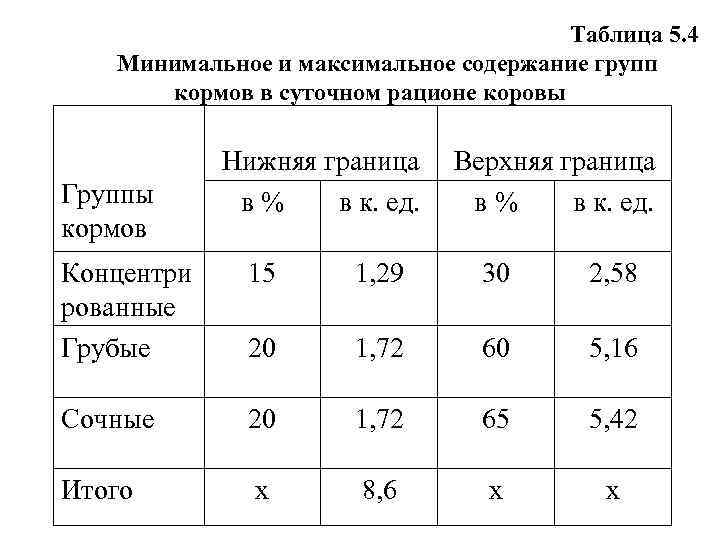
Таблица 5. 4 Минимальное и максимальное содержание групп кормов в суточном рационе коровы Группы кормов Нижняя граница в% в к. ед. Верхняя граница в% в к. ед. Концентри рованные Грубые 15 1, 29 30 2, 58 20 1, 72 60 5, 16 Сочные 20 1, 72 65 5, 42 Итого х 8, 6 х х

3. Подготовка входной информации Приведенные в таблицах 5. 1 -5. 4 показатели используются при построении числовой экономико-математической модели в качестве технико-экономических коэффициентов, оценок переменных в целевой функции и констант.

3. Подготовка входной информации Дополнительные условия: Масса отдельных групп кормов в рационе может колебаться в пределах: • Концентрированные корма – 2 -3 кг; • Грубые – 10 -15 кг; • Силос – 12 -20 кг; • Корнеклубнеплоды – 5 -8 кг. Сена в рационе должно быть не менее 50% общего количества кормовых единиц; сенажа – не менее 3 и не более 8%; ячмень должен составлять не менее 60% концентрированных кормов.

3. Подготовка входной информации Рацион должен полностью удовлетворять потребность коровы во всех перечисленных питательных веществах при заданном соотношении отдельных видов и групп кормов и одновременно иметь минимальную стоимость.

4. Построение числовой экономикоматематической модели Числовая экономико-математическая модель представляет собой систему уравнений и неравенств. При этом буквенно-символьные обозначения коэффициентов и свободных членов структурной записи заменяются числовыми величинами.

4. Построение числовой экономикоматематической модели Обозначим переменные следующим образом: х1 - количество ячменя в рационе, кг; х2 – количество отрубей в рационе, кг; х3 - количество шрота в рационе, кг; х4 – количество пшеничной соломы в рационе, кг; х5 – количество ячменной соломы в рационе, кг; х6 – количество просяной соломы в рационе, кг; х7 – количество сена суданкового в рационе, кг; х8 – количество сенажа в рационе, кг; х9 – количество силоса в рационе, кг; х10 – количество свёклы кормовой в рационе, кг;

4. Построение числовой экономикоматематической модели По экономическому содержанию и характеру формализации в модели можно выделить следующие группы ограничений: 1) по балансу питательных веществ; 2)по удельному весу групп кормов в рационе; 3)по удельному весу видов кормов внутри групп.

4. Построение числовой экономикоматематической модели Первая группа ограничений отражает требования к рациону по питательным веществам и показывает, что он должен содержать питательное вещество не менее требуемого по норме количества. 1 -е ограничение по кормовым единицам: 1)1, 15 х1 + 0, 75 х2 + 1, 03 х3 +…+0, 12 х10 8, 6 2 -е ограничение по обменной энергии: 2)10, 5 х1 +9, 41 х2 + 9, 87 х3 +…+ 1, 65 х10 104 3 -е ограничение по сухому веществу: 3)0, 85 х1 + 0, 85 х2 + 0, 9 х3+…+0, 12 х12≥ 12, 3 4 -е ограничение по сырому протеину: 4)113 х1 + 151 х2 + 429 х3 + … + 13 х10≥ 1200

4. Построение числовой экономикоматематической модели 5 -е ограничение по переваримому протеину: 5)85 х1+97 х2+386 х3+…+9 х10≥ 940 6 -е ограничение по кальцию: 6)2 х1+2 х2+3, 6 х3+…+0, 4 х10≥ 57 7 -е ограничение по фосфору: 7)3, 9 х1 + 9, 6 х2 + 12, 2 х3 + … +0, 5 х10≥ 39 8 -е ограничение по железу: 8)50 х1 + 170 х2 + 332 х3 + … + 8 х10≥ 690 9 -е ограничение по каротину: 9)0, 5 х1 + 2, 6 х2 + 3 х3 + … + 0, 1 х10≥ 345

4. Построение числовой экономикоматематической модели Первое ограничение означает, что питательность всех кормов в рационе не должна быть меньше 8, 6 к. ед. , второе, что рацион должен содержать не менее 104 МДж обменной энергии. Третье – девятое ограничения содержат условия по минимальному содержанию других элементов питания в рационе.

4. Построение числовой экономикоматематической модели Коэффициентами при переменных в первом ограничении являются содержание кормовых единиц в 1 кг корма разных видов, во втором ограничении – содержание обменной энергии в 1 кг корма, в третьем-девятом ограничениях – содержание соответствующих питательных веществ в 1 кг корма; свободными членами неравенств – минимальная суточная потребность одной головы в кормовых единицах, обменной энергии и других элементах питания.

4. Построение числовой экономикоматематической модели Вторая группа ограничений отражает физиологически допустимые пределы скармливания групп кормов. Эти дополнительные ограничения показывают нижние (минимальные) и верхние (максимальные) границы по каждой группе кормов.

4. Построение числовой экономикоматематической модели • 10 -е ограничение по минимальной границе содержания концентрированных кормов в рационе – их должно быть не меньше 15% питательности рациона: 10) 1, 15 х1 +0, 75 х2 +1, 03 х3 >= 1, 29 • 11 -е ограничение по минимальной границе содержания грубых кормов в рационе: 11)0, 22 х4 +0, 34 х5 + 0, 4 х6 + 0, 57 х7 + 0, 35 х8 >=1, 72 • 12 -е ограничение – по минимальной границе содержания сочных кормов в рационе: 12) 0, 2 х9 + 0, 12 х10>= 1, 72

4. Построение числовой экономикоматематической модели • 13 -е ограничение – по максимальной границе содержания концентрированных кормов в рационе: 13)1, 15 х1 +0, 75 х2 +1, 03 х3<=2, 58 • 14 -е ограничение – по максимальной границе содержания грубых кормов в рационе: 14) 0, 22 х4 +0, 34 х5 + 0, 4 х6 + 0, 57 х7 + 0, 35 х8<=5, 16 • 15 -е ограничение – по максимальной границе содержания сочных кормов в рационе: 15)0, 2 х9 + 0, 12 х10 5, 42

4. Построение числовой экономикоматематической модели Третья группа ограничений отражает физиологические, зоотехнические или экономические требования по удельному весу отдельных видов кормов внутри однородных групп. Коэффициентами при переменных в этих ограничениях выступают доли отдельных видов кормов. Так, 16 -е ограничение записывается следующим образом: 16) – 0, 4 х1 +0, 6 х2 + 0, 6 х3 0 Оно означает, что ячменя в составе концентрированных кормов должно быть не меньше 60%.

4. Построение числовой экономикоматематической модели 17 -е ограничение фиксирует условие по включению в рацион шрота (не менее 10%): 17) 0, 1 х1 + 0, 1 х2 - 0, 9 х3 0 18 -е и 19 -е ограничения по соотношению видов соломы в рационе: 18)х4 -0, 5 х5 - 0, 5 х6 0 19)0, 75 х6 – 0, 25 х5 0 20 -е ограничение – корнеплоды в составе сочных кормов должны занимать не менее 10%: 20) 0, 1 х9 – 0, 9 х10= 0

4. Построение числовой экономикоматематической модели 21 -е ограничение – сена в составе грубых кормов должно быть не менее 50: 21)0, 5 х4 +0, 5 х5+0, 5 х6+0, 5 х8– 0, 5 х7 = 0 22 -е ограничение по удельному весу отрубей в составе концентрированных кормов: 22)0, 1 х1 -0, 9 х2+0, 1 х3=0 23 -е ограничение – сенаж должен составлять не менее 3% питательности рациона: 23)0, 07 х1+0, 07 х2+0, 07 х3+0, 07 х4 +0, 07 х5+0, 07 х6+0, 07 х7– -0, 93 х8 +0, 07 х9 +0, 07 х10 = 0

4. Построение числовой экономикоматематической модели Целевая функция записывается так: 2, 92 х1+3, 2 х2+4, 2 х3+0, 2 х4+0, 2 х5+0, 2 х6+1, 13 х 7+0, 38 х8+0, 21 х9+0, 2 х10 min Записанная в виде матрицы экономикоматематическая модель приведена в приложении 1.
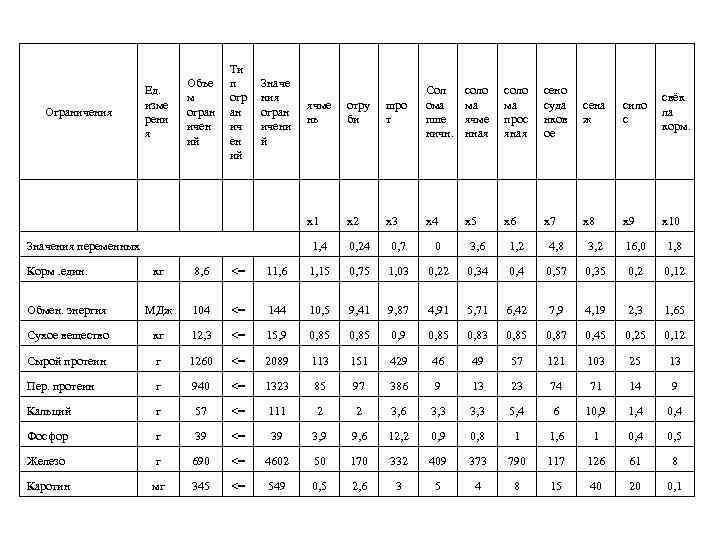
Ти п огр ан ич ен ий Значе ния огран ичени й Значения переменных Корм. един. ячме нь отру би шро т Сол ома пше ничн. х1 Ограничения Ед. изме рени я Объе м огран ичен ий х2 х3 х4 соло ма ячме нная соло ма прос яная сено суда нков ое сена ж сило с свёк ла корм. х5 х6 х7 х8 х9 х10 1, 4 0, 24 0, 7 0 3, 6 1, 2 4, 8 3, 2 16, 0 1, 8 кг 8, 6 <= 11, 6 1, 15 0, 75 1, 03 0, 22 0, 34 0, 57 0, 35 0, 2 0, 12 Обмен. энергия МДж 104 <= 144 10, 5 9, 41 9, 87 4, 91 5, 71 6, 42 7, 9 4, 19 2, 3 1, 65 Сухое вещество кг 12, 3 <= 15, 9 0, 85 0, 83 0, 85 0, 87 0, 45 0, 25 0, 12 Сырой протеин г 1260 <= 2089 113 151 429 46 49 57 121 103 25 13 Пер. протеин г 940 <= 1323 85 97 386 9 13 23 74 71 14 9 Кальций г 57 <= 111 2 2 3, 6 3, 3 5, 4 6 10, 9 1, 4 0, 4 Фосфор г 39 <= 39 3, 9 9, 6 12, 2 0, 9 0, 8 1 1, 6 1 0, 4 0, 5 Железо г 690 <= 4602 50 170 332 409 373 790 117 126 61 8 Каротин мг 345 <= 549 0, 5 2, 6 3 5 4 8 15 40 20 0, 1

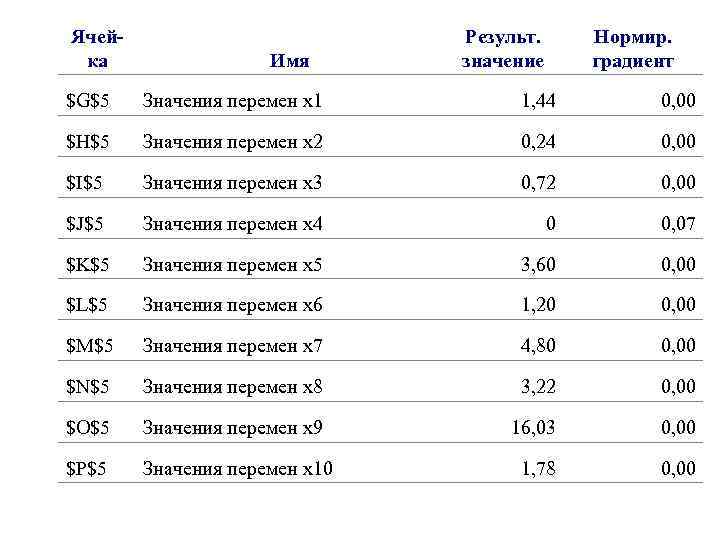
5. Анализ результатов решения задачи Разработанная экономико-математическая модель была перенесена на лист MS Excel и решена на персональном компьютере с помощью программного средства Microsoft Excel. Переменные получили значения, которые приведены в строке матрицы «Значения переменных» .

5. Анализ результатов решения задачи В результате решения задачи определилось количество кормов в рационе коровы. Полученный оптимальный рацион кормления представлен в таблице 5. 5.
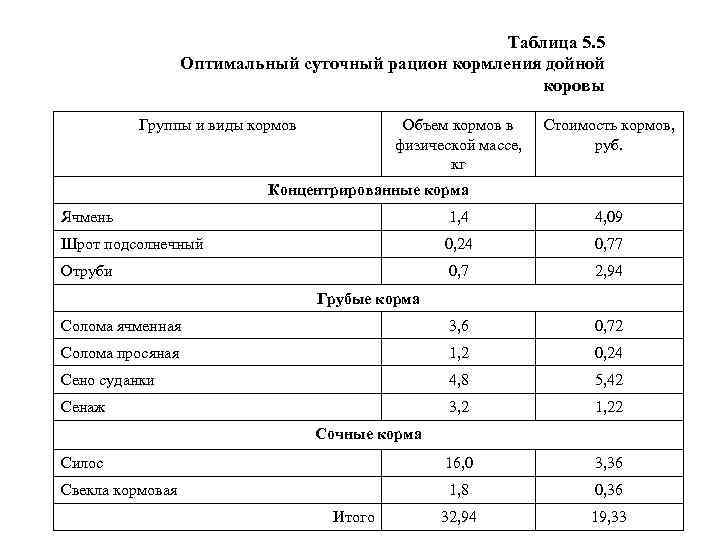
Таблица 5. 5 Оптимальный суточный рацион кормления дойной коровы Группы и виды кормов Объем кормов в физической массе, кг Стоимость кормов, руб. Концентрированные корма Ячмень 1, 4 4, 09 Шрот подсолнечный 0, 24 0, 77 Отруби 0, 7 2, 94 Солома ячменная 3, 6 0, 72 Солома просяная 1, 2 0, 24 Сено суданки 4, 8 5, 42 Сенаж 3, 2 1, 22 Силос 16, 0 3, 36 Свекла кормовая 1, 8 0, 36 32, 94 19, 33 Грубые корма Сочные корма Итого

5. Анализ результатов решения задачи Как видим, в состав рациона вошли почти все виды кормов (кроме соломы пшеничной), которыми располагает хозяйство. Составленный из имеющихся в хозяйстве кормов рацион имеет минимальную стоимость. Вошедшее в состав рациона количество кормов удовлетворяет суточную потребность животного в питательных веществах, что видно из таблицы 5. 6.
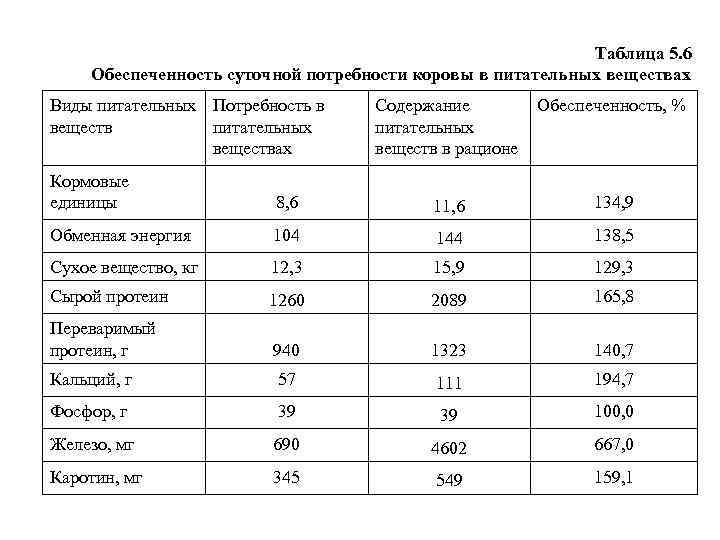
Таблица 5. 6 Обеспеченность суточной потребности коровы в питательных веществах Виды питательных Потребность в веществ питательных веществах Содержание питательных веществ в рационе Обеспеченность, % Кормовые единицы 8, 6 11, 6 134, 9 Обменная энергия 104 144 138, 5 Сухое вещество, кг 12, 3 15, 9 129, 3 Сырой протеин 1260 2089 165, 8 Переваримый протеин, г 940 1323 140, 7 Кальций, г 57 111 194, 7 Фосфор, г 39 39 100, 0 Железо, мг 690 4602 667, 0 Каротин, мг 345 549 159, 1

5. Анализ результатов решения задачи Данные таблицы показывают, что полученный в результате решения задачи кормовой рацион полностью удовлетворяет потребность животного во всех видах питательных веществ. По всем питательным веществам, кроме фосфора, наблюдается превышение содержания в кормах над потребностью. Лишь по фосфору – 100 -процентная обеспеченность.

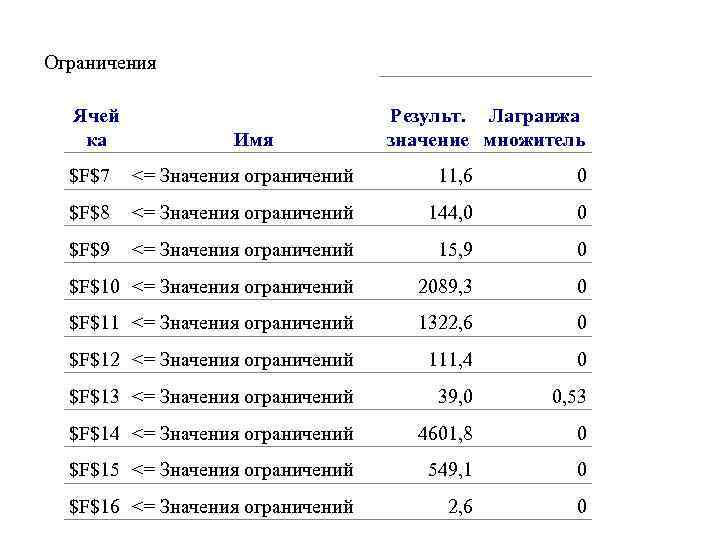
5. Анализ результатов решения задачи Недостаток фосфора в кормах, имеющихся в хозяйстве, ведет к тому, что в рацион включается дополнительное количество кормов, удорожающих его. Поэтому, чтобы избежать перерасхода кормов, необходимо включать в рацион животного минеральные добавки, содержащие фосфор, например, преципитат. Компьютер выдаёт Отчёт по устойчивости, который содержит двойственные оценки, позволяющие дать оценку кормов.
Ячейка Имя Результ. значение Нормир. градиент $G$5 Значения перемен х1 1, 44 0, 00 $H$5 Значения перемен х2 0, 24 0, 00 $I$5 Значения перемен х3 0, 72 0, 00 $J$5 Значения перемен х4 0 0, 07 $K$5 Значения перемен х5 3, 60 0, 00 $L$5 Значения перемен х6 1, 20 0, 00 $M$5 Значения перемен х7 4, 80 0, 00 $N$5 Значения перемен х8 3, 22 0, 00 $O$5 Значения перемен х9 16, 03 0, 00 $P$5 Значения перемен х10 1, 78 0, 00
Ограничения Ячей ка Имя Результ. Лагранжа значение множитель $F$7 <= Значения ограничений 11, 6 0 $F$8 <= Значения ограничений 144, 0 0 $F$9 <= Значения ограничений 15, 9 0 $F$10 <= Значения ограничений 2089, 3 0 $F$11 <= Значения ограничений 1322, 6 0 $F$12 <= Значения ограничений 111, 4 0 $F$13 <= Значения ограничений 39, 0 0, 53 $F$14 <= Значения ограничений 4601, 8 0 $F$15 <= Значения ограничений 549, 1 0 $F$16 <= Значения ограничений 2, 6 0
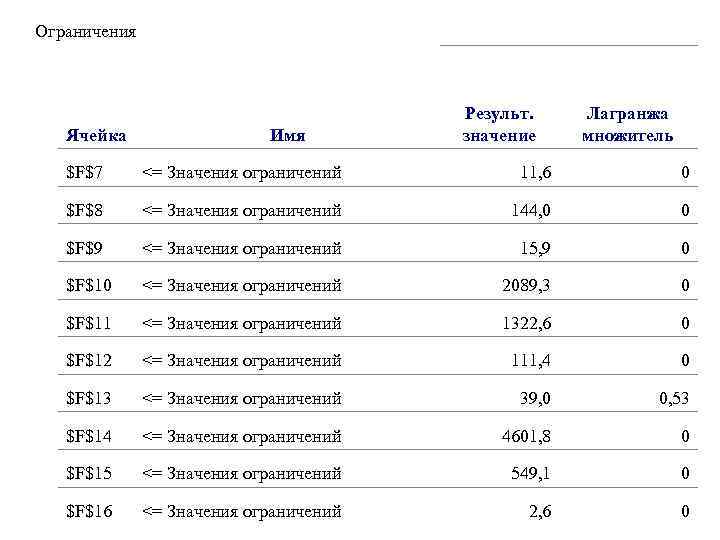
Ограничения Ячейка Имя Результ. значение Лагранжа множитель $F$7 <= Значения ограничений 11, 6 0 $F$8 <= Значения ограничений 144, 0 0 $F$9 <= Значения ограничений 15, 9 0 $F$10 <= Значения ограничений 2089, 3 0 $F$11 <= Значения ограничений 1322, 6 0 $F$12 <= Значения ограничений 111, 4 0 $F$13 <= Значения ограничений 39, 0 0, 53 $F$14 <= Значения ограничений 4601, 8 0 $F$15 <= Значения ограничений 549, 1 0 $F$16 <= Значения ограничений 2, 6 0
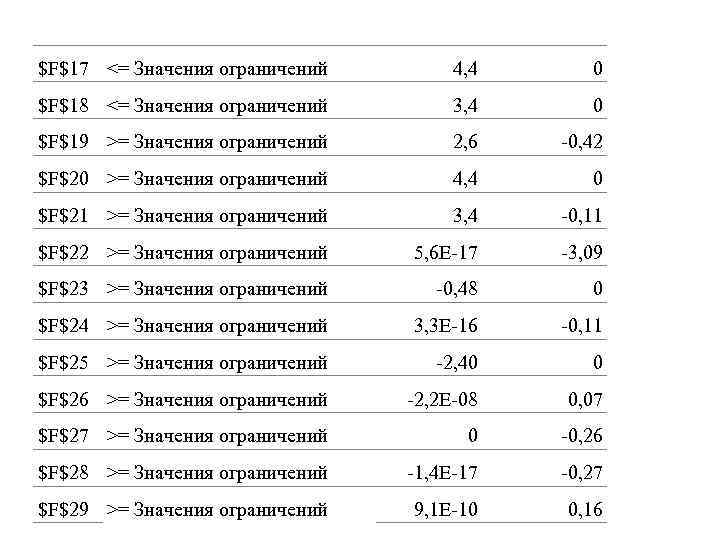
$F$17 <= Значения ограничений 4, 4 0 $F$18 <= Значения ограничений 3, 4 0 $F$19 >= Значения ограничений 2, 6 -0, 42 $F$20 >= Значения ограничений 4, 4 0 $F$21 >= Значения ограничений 3, 4 -0, 11 $F$22 >= Значения ограничений 5, 6 E-17 -3, 09 $F$23 >= Значения ограничений -0, 48 0 $F$24 >= Значения ограничений 3, 3 E-16 -0, 11 $F$25 >= Значения ограничений -2, 40 0 $F$26 >= Значения ограничений -2, 2 E-08 0, 07 $F$27 >= Значения ограничений 0 -0, 26 $F$28 >= Значения ограничений -1, 4 E-17 -0, 27 $F$29 >= Значения ограничений 9, 1 E-10 0, 16
рац. кормл.ppt