Лекция 5 Поверхности Следует рассматривать поверхность как

Лекция 5 Поверхности

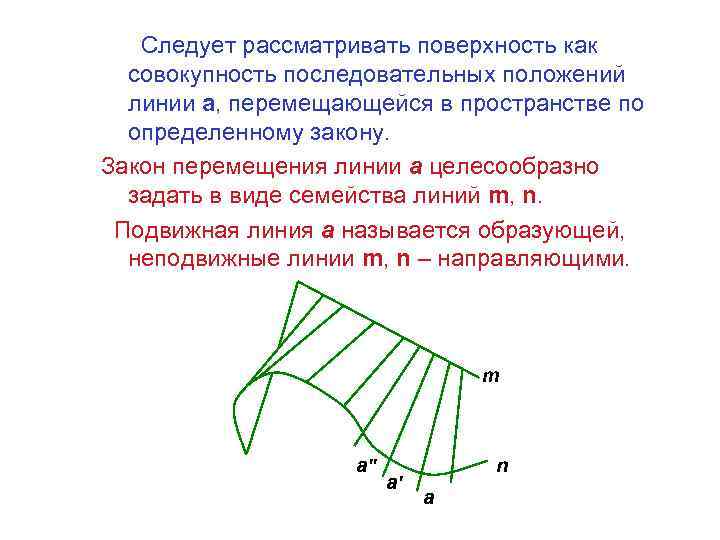Следует рассматривать поверхность как совокупность последовательных положений линии a, перемещающейся в пространстве по определенному закону. Закон перемещения линии а целесообразно задать в виде семейства линий m, n. Подвижная линия а называется образующей, неподвижные линии m, n – направляющими. m a'' a' n a

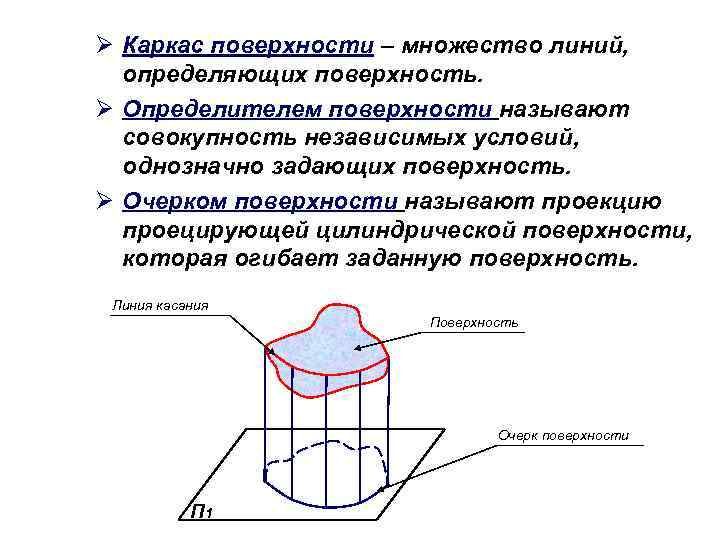Ø Каркас поверхности – множество линий, определяющих поверхность. Ø Определителем поверхности называют совокупность независимых условий, однозначно задающих поверхность. Ø Очерком поверхности называют проекцию проецирующей цилиндрической поверхности, которая огибает заданную поверхность. Линия касания Поверхность Очерк поверхности П 1

Основой классификации поверхностей могут служить их определители или геометрические особенности, связанные с кинематическим способом образования. Важными признаками формообразования поверхностей являются: • Вид образующей; • Постоянство образующей; • Закон перемещения образующей; • Развёртываемость куска поверхности.

Классификация поверхностей По виду образующей: • Линейчатые • Нелинейчатые По постоянству образующей: • С постоянной образующей • С переменной образующей По закону движения образующей: • Кинематические поверхности • Поверхности вращения • Винтовые поверхности По развёртываемости: • Развёртываемые • Не развёртываемые

Линейчатые развёртываемые поверхности Цилиндрические поверхности Ф(a, m, s) [a ∩ m, a II s], m-кривая направляющая s-направляющий вектор Если m-окружность и m⊥a, то поверхностью будет прямой круговой цилиндр. s a a a' a' a'' m a''''

Призматические поверхности Ф(a, m, s) [a ∩ m, a II s] m-ломаная линия s-направляющий вектор a s a''' a' a'' m

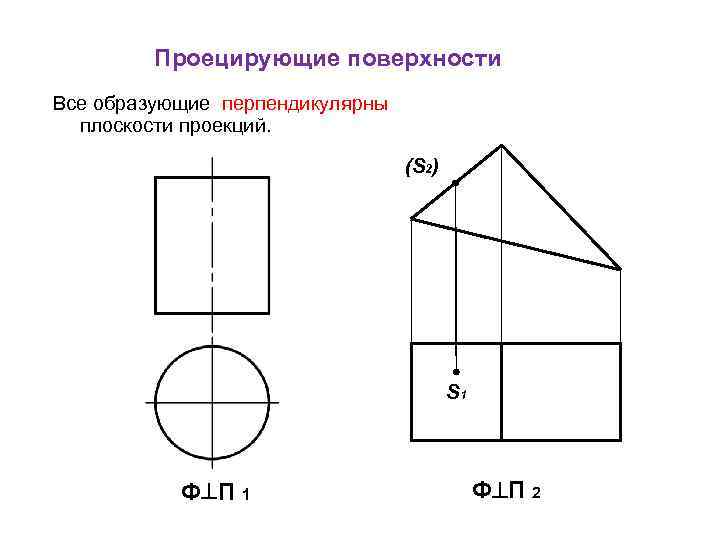Проецирующие поверхности Все образующие перпендикулярны плоскости проекций. (S 2) S 1 Ф П 2

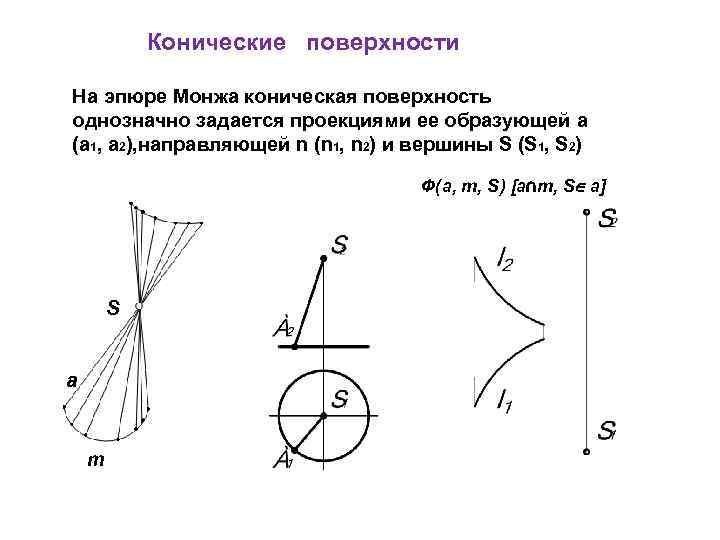Конические поверхности На эпюре Монжа коническая поверхность однозначно задается проекциями ее образующей a (a 1, a 2), направляющей n (n 1, n 2) и вершины S (S 1, S 2) Ф(a, m, S) [a∩m, S∈ a] S a m

Пирамидальные поверхности Ф(a, m, S) [a∩m, S∈ a] S a''' a a' m a''

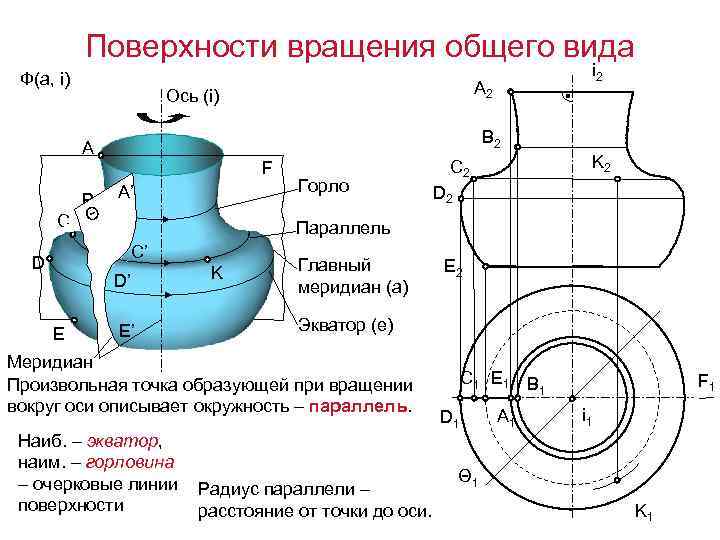Поверхности вращения общего вида Ф(а, i) B 2 F B A’ C Θ B’ D’ E’ Горло K Главный меридиан (а) D 2 E 2 Экватор (е) Меридиан Произвольная точка образующей при вращении вокруг оси описывает окружность – параллель. Наиб. – экватор, наим. – горловина – очерковые линии поверхности K 2 C 2 Параллель C’ E A 2 Ось (i) A D i 2 Радиус параллели – расстояние от точки до оси. C 1 E 1 B 1 D 1 A 1 F 1 i 1 Θ 1 K 1

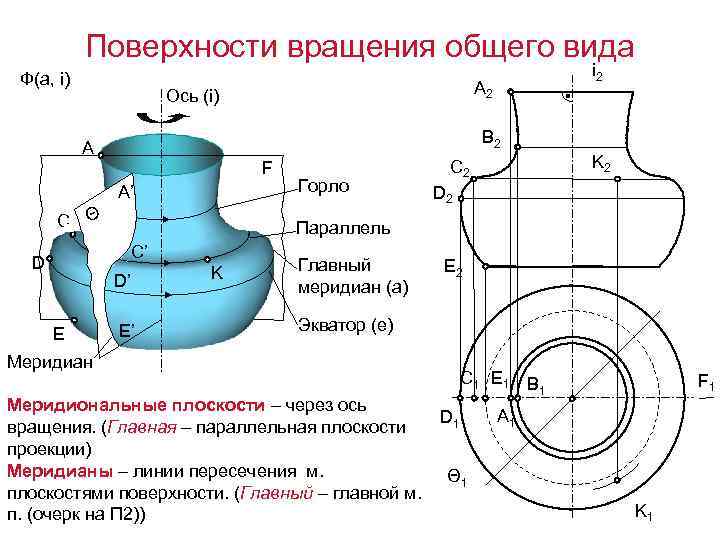Поверхности вращения общего вида Ф(а, i) A 2 Ось (i) B 2 A C F A’ Θ B’ D’ E E’ Горло K 2 C 2 D 2 Параллель C’ D i 2 K Главный меридиан (а) E 2 Экватор (е) Меридиан Меридиональные плоскости – через ось вращения. (Главная – параллельная плоскости проекции) Меридианы – линии пересечения м. плоскостями поверхности. (Главный – главной м. п. (очерк на П 2)) C 1 E 1 B 1 D 1 F 1 A 1 Θ 1 K 1

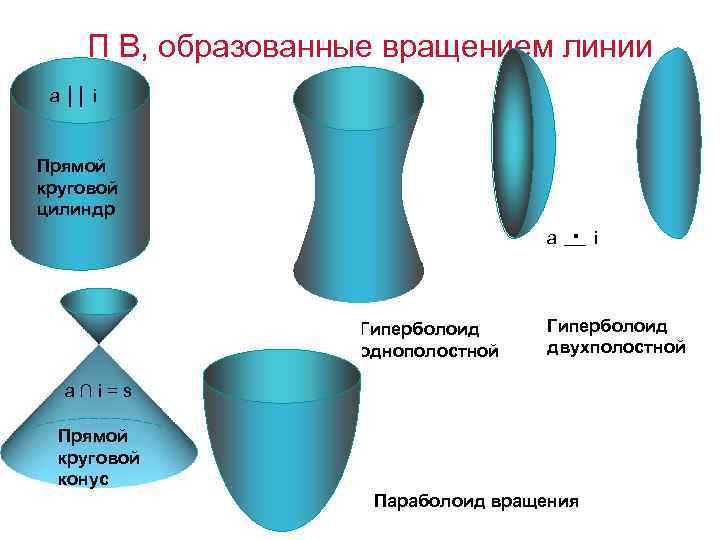П В, образованные вращением линии a ││ i Прямой круговой цилиндр a Гиперболоид однополостной i Гиперболоид двухполостной a∩i=s Прямой круговой конус Параболоид вращения

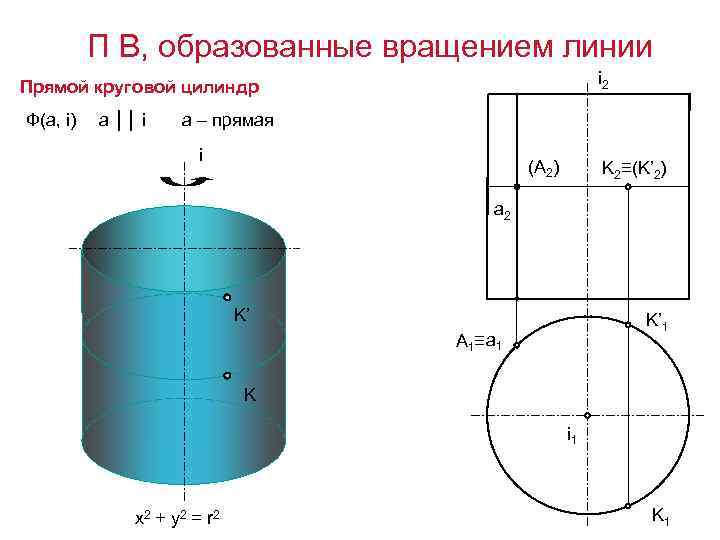П В, образованные вращением линии i 2 Прямой круговой цилиндр Ф(а, i) a ││ i а – прямая i (A 2) K 2≡(K’ 2) a 2 K’ K’ 1 A 1 ≡ a 1 K i 1 x 2 + y 2 = r 2 K 1

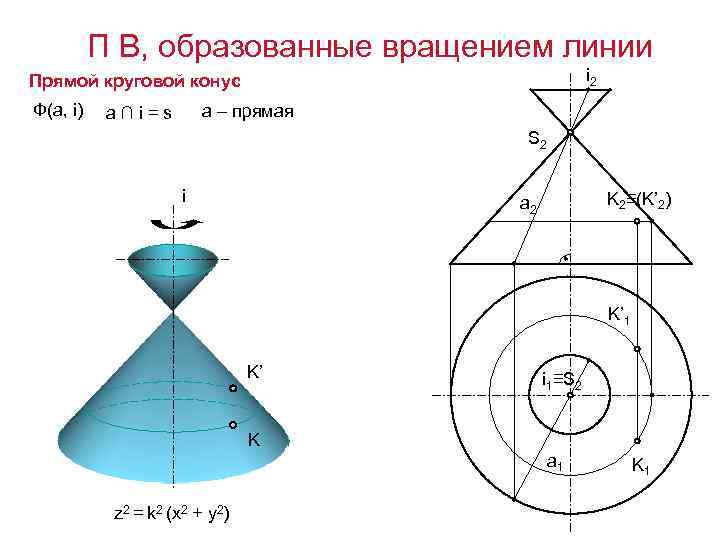П В, образованные вращением линии i 2 Прямой круговой конус Ф(а, i) а – прямая a∩i=s S 2 i K 2≡(K’ 2) a 2 K’ 1 K’ i 1≡S 2 K a 1 z 2 = k 2 (x 2 + y 2) K 1

П В, образованные вращением окружности t=0 t˂R Сфера Тор закрытый t>R Тор открытый

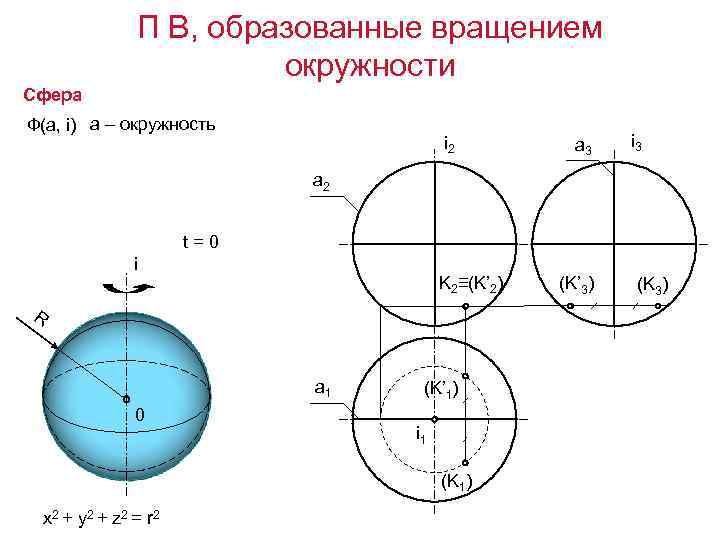П В, образованные вращением окружности Сфера Ф(а, i) а – окружность i 2 a 3 i 3 a 2 t=0 i K 2≡(K’ 2) R a 1 0 (K’ 1) i 1 (K 1) x 2 + y 2 + z 2 = r 2 (K’ 3) (K 3)

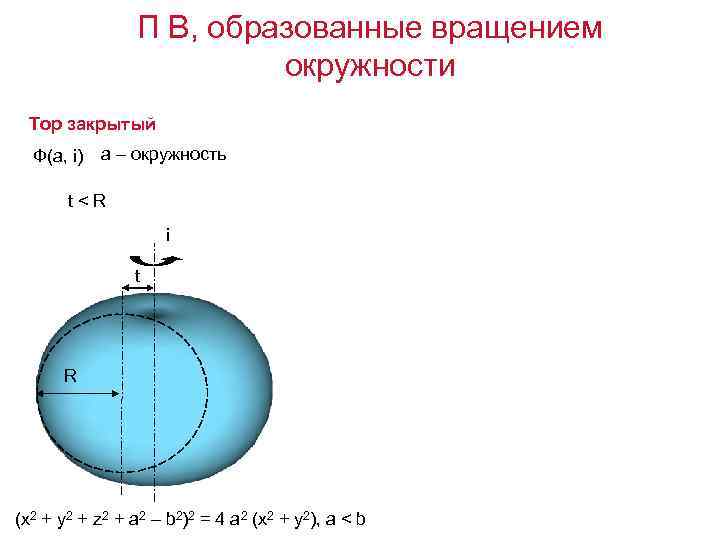П В, образованные вращением окружности Тор закрытый Ф(а, i) а – окружность t

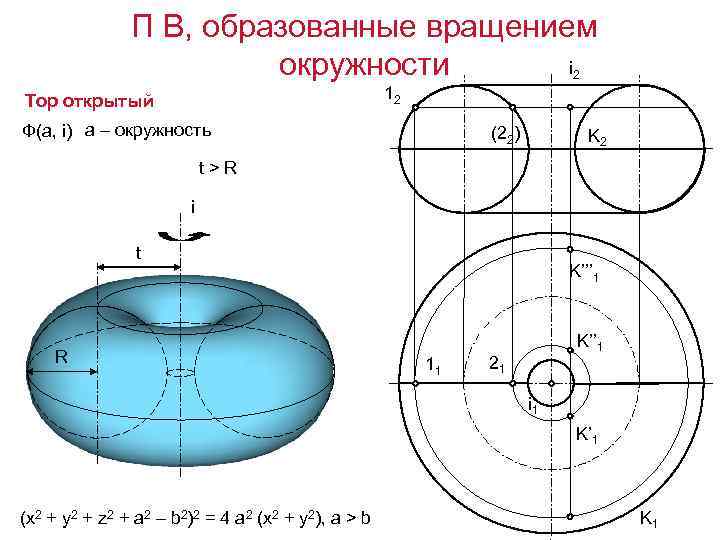П В, образованные вращением i окружности 2 12 Тор открытый Ф(а, i) а – окружность (22) K 2 t>R i t R 0 K’’’ 1 11 K’’ 1 21 i 1 K’ 1 (x 2 + y 2 + z 2 + a 2 – b 2)2 = 4 a 2 (x 2 + y 2), a > b K 1

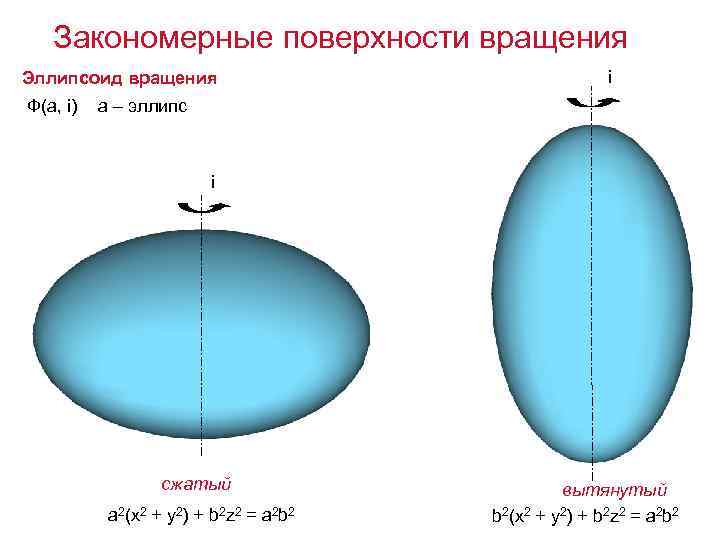Закономерные поверхности вращения Эллипсоид вращения Ф(а, i) i а – эллипс i сжатый a 2(x 2 + y 2) + b 2 z 2 = a 2 b 2 вытянутый b 2(x 2 + y 2) + b 2 z 2 = a 2 b 2

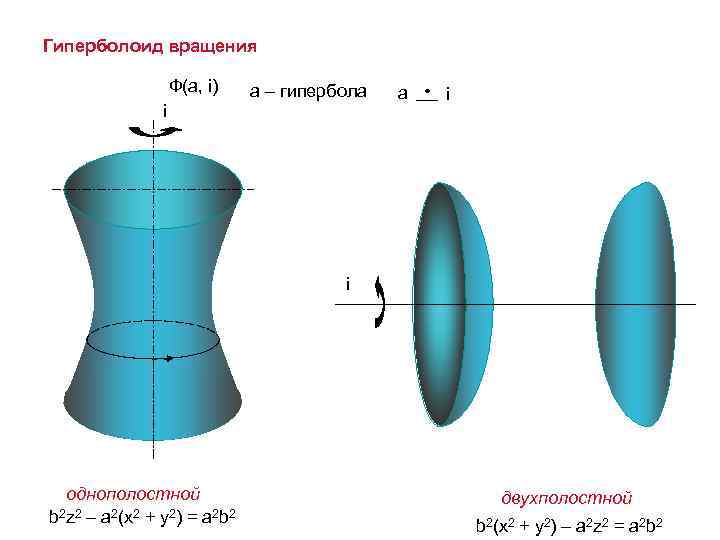Гиперболоид вращения Ф(а, i) i а – гипербола a i i однополостной b 2 z 2 – a 2(x 2 + y 2) = a 2 b 2 двухполостной b 2(x 2 + y 2) – a 2 z 2 = a 2 b 2

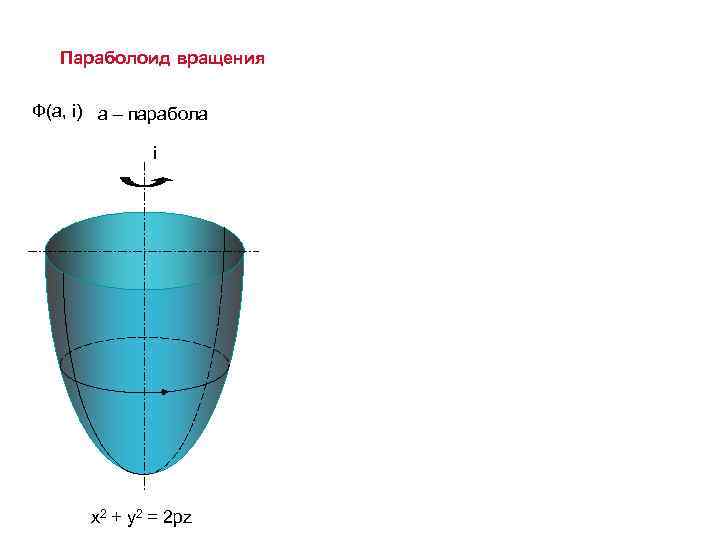Параболоид вращения Ф(а, i) а – парабола i x 2 + y 2 = 2 pz