Лекция 5 Пересечение прямой и плоскости

Лекция № 5

Пересечение прямой и плоскости • Если прямая не лежит в плоскости и не параллельна ей, то она пересекает плоскость и имеет с ней одну общую точку. • • Правила построения точки пересечения прямой и плоскости: Заключают прямую во вспомогательную плоскость ( как правило, вспомогательная плоскость – проецирующая). Строят линию пересечения заданной и вспомогательной плоскостей. Определяют искомую точку на пересечении заданной прямой и построенной линии пересечения плоскостей.

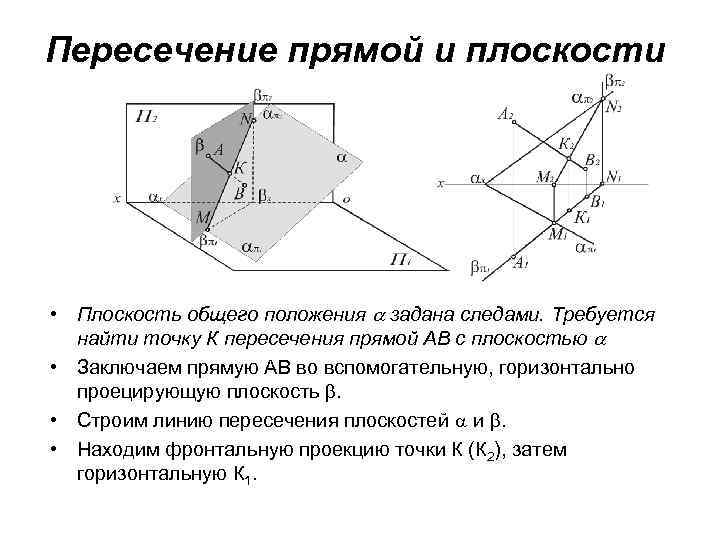Пересечение прямой и плоскости • Плоскость общего положения задана следами. Требуется найти точку К пересечения прямой АВ с плоскостью • Заключаем прямую АВ во вспомогательную, горизонтально проецирующую плоскость . • Строим линию пересечения плоскостей и . • Находим фронтальную проекцию точки К (К 2), затем горизонтальную К 1.

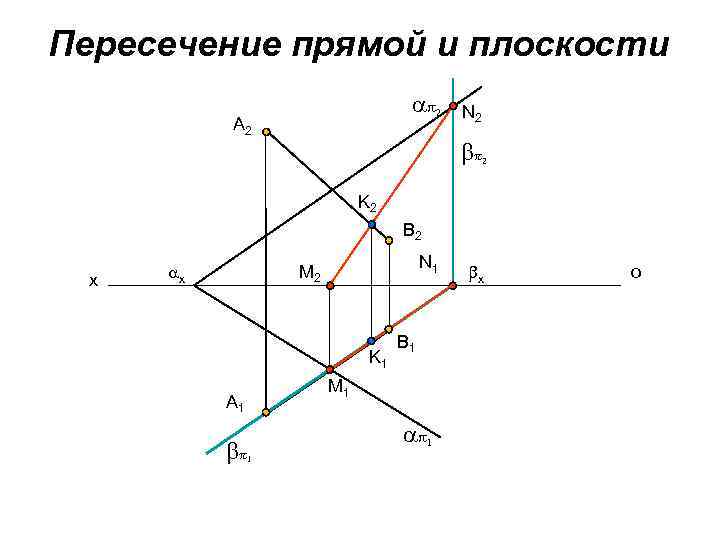Пересечение прямой и плоскости 2 A 2 N 2 2 K 2 B 2 x x N 1 M 2 K 1 M 1 A 1 B 1 1 1 x o

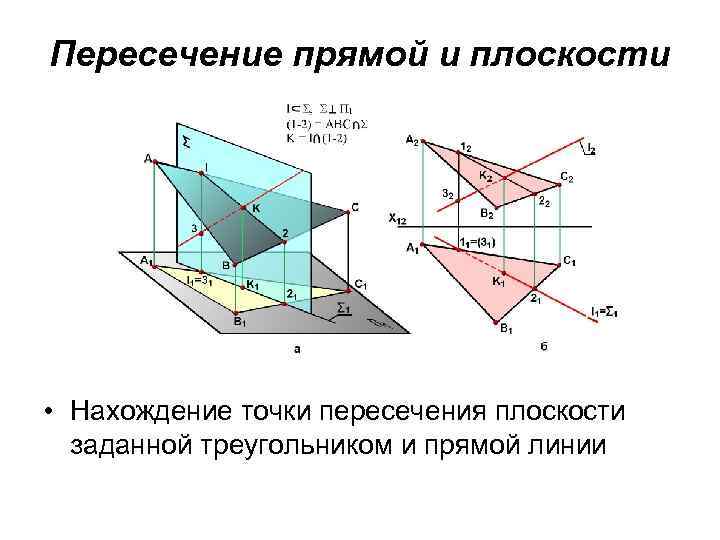Пересечение прямой и плоскости • Нахождение точки пересечения плоскости заданной треугольником и прямой линии

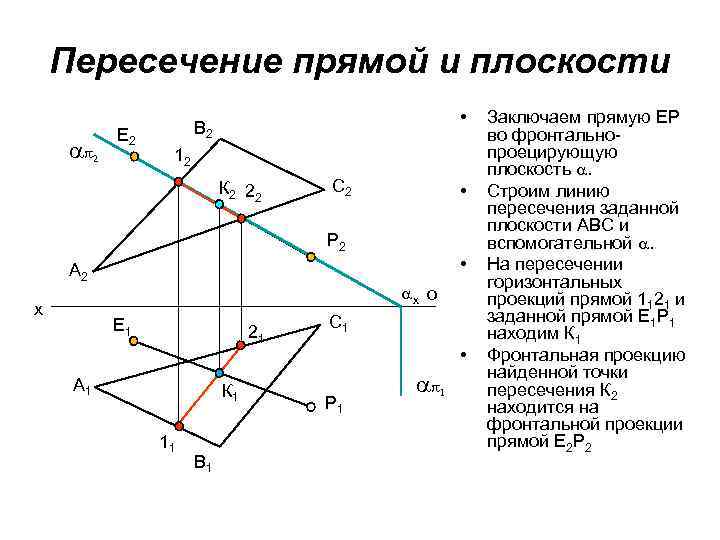Пересечение прямой и плоскости 2 E 2 • B 2 12 К 2 22 C 2 • P 2 • A 2 x x o E 1 21 A 1 К 1 11 B 1 C 1 • P 1 1 Заключаем прямую ЕР во фронтальнопроецирующую плоскость . Строим линию пересечения заданной плоскости АВС и вспомогательной . На пересечении горизонтальных проекций прямой 1121 и заданной прямой Е 1 Р 1 находим К 1 Фронтальная проекцию найденной точки пересечения К 2 находится на фронтальной проекции прямой Е 2 Р 2

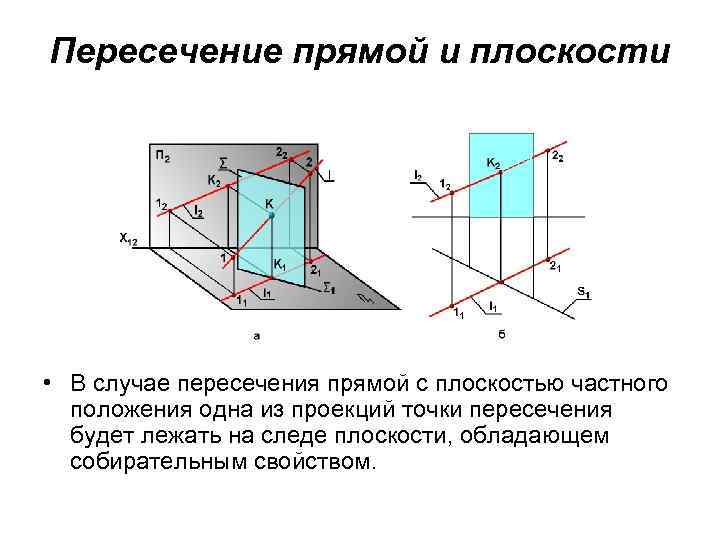Пересечение прямой и плоскости • В случае пересечения прямой с плоскостью частного положения одна из проекций точки пересечения будет лежать на следе плоскости, обладающем собирательным свойством.

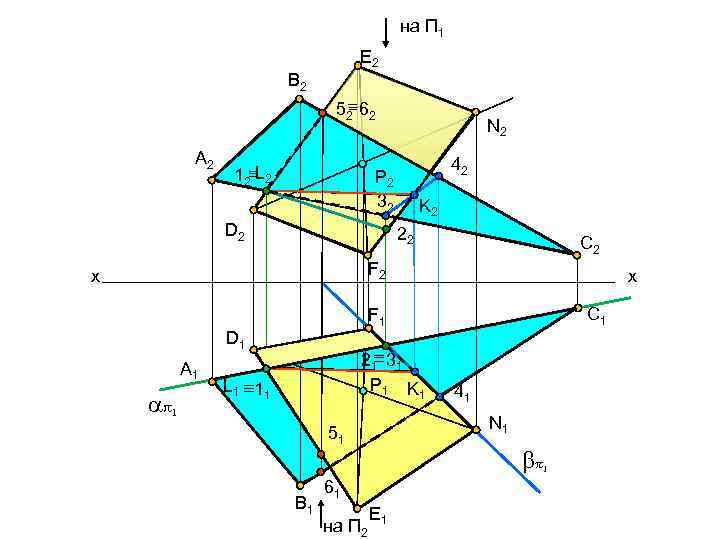
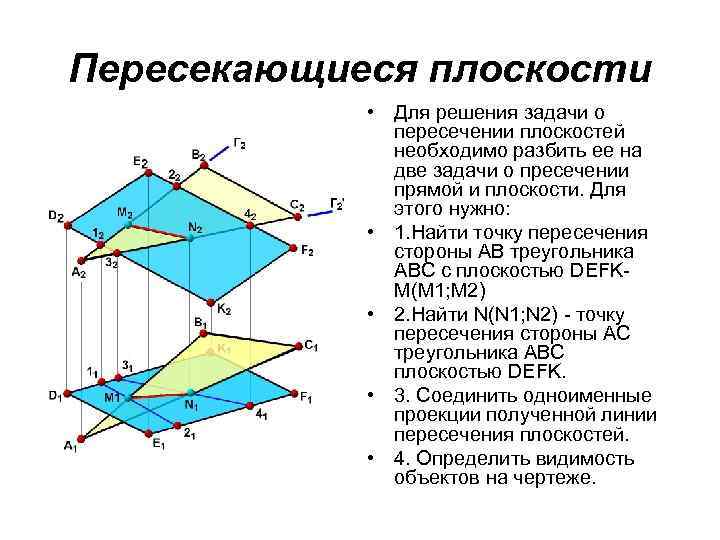Пересекающиеся плоскости • Для решения задачи о пересечении плоскостей необходимо разбить ее на две задачи о пресечении прямой и плоскости. Для этого нужно: • 1. Найти точку пересечения стороны АВ треугольника АВС с плоскостью DEFKМ(М 1; М 2) • 2. Найти N(N 1; N 2) - точку пересечения стороны АС треугольника АВС плоскостью DEFK. • 3. Соединить одноименные проекции полученной линии пересечения плоскостей. • 4. Определить видимость объектов на чертеже.

на П 1 E 2 B 2 52 62 A 2 12 L 2 N 2 42 P 2 32 D 2 K 2 22 C 2 F 2 x 1 C 1 F 1 D 1 A 1 x 21 31 P 1 K 1 L 1 11 N 1 51 B 1 61 на П 2 41 E 1 1

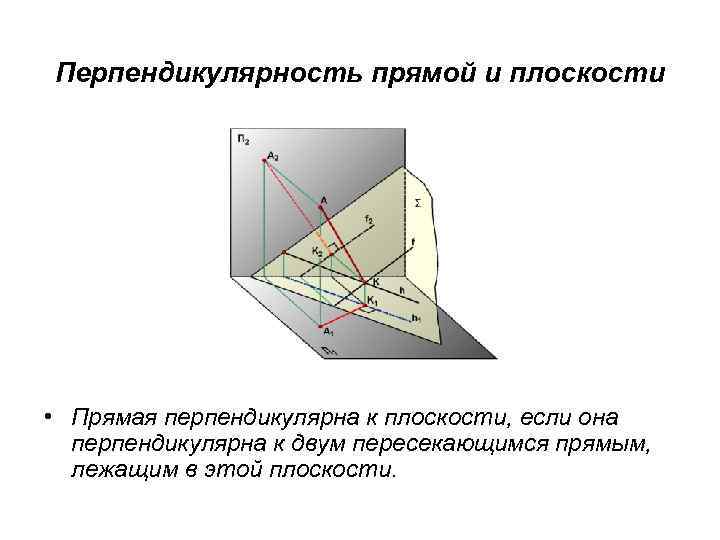Перпендикулярность прямой и плоскости • Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости.

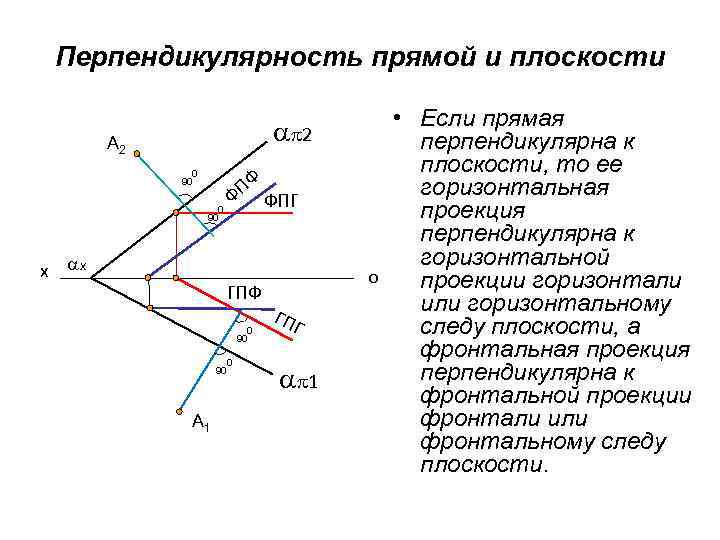Перпендикулярность прямой и плоскости 2 A 2 0 90 х х ПФ Ф ФПГ ГПФ 0 90 A 1 ГПГ 1 • Если прямая перпендикулярна к плоскости, то ее горизонтальная проекция перпендикулярна к горизонтальной о проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальной проекции фронтали или фронтальному следу плоскости.

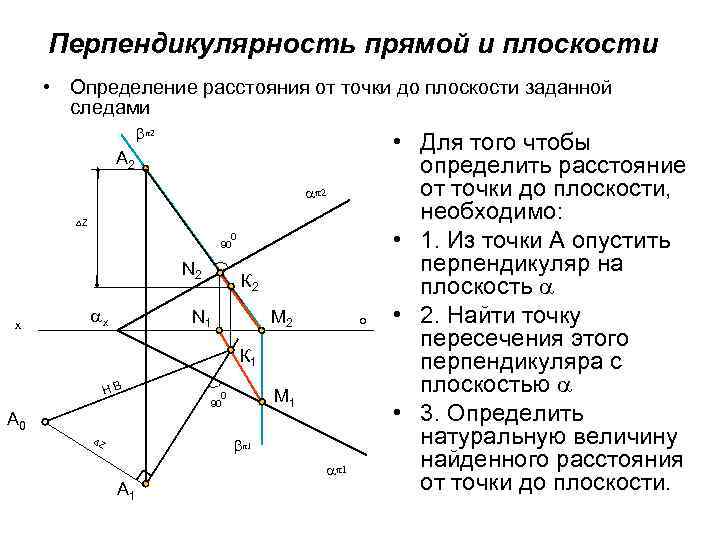Перпендикулярность прямой и плоскости • Определение расстояния от точки до плоскости заданной следами 2 A 2 2 DZ 0 90 N 2 x x К 2 N 1 M 2 o К 1 НВ M 1 0 90 A 0 DZ 1 1 A 1 • Для того чтобы определить расстояние от точки до плоскости, необходимо: • 1. Из точки А опустить перпендикуляр на плоскость • 2. Найти точку пересечения этого перпендикуляра с плоскостью • 3. Определить натуральную величину найденного расстояния от точки до плоскости.

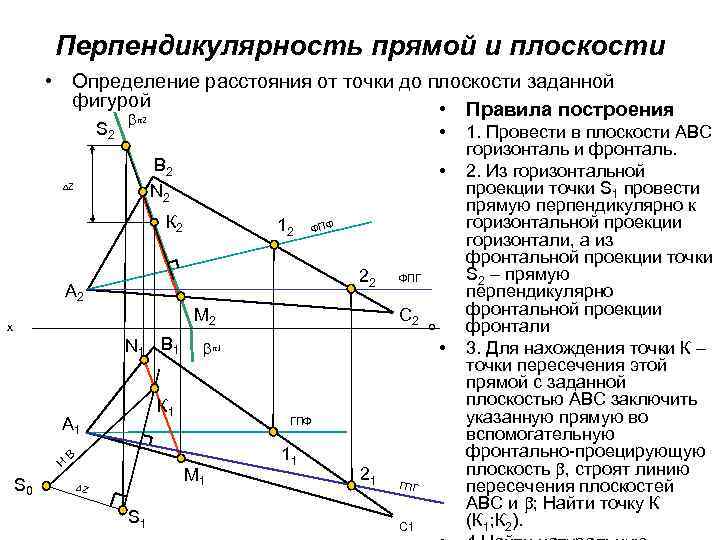Перпендикулярность прямой и плоскости • Определение расстояния от точки до плоскости заданной фигурой • Правила построения S 2 2 • B 2 N 2 DZ • К 2 12 ФПФ 22 A 2 М 2 x N 1 B 1 Н S 0 М 1 S 1 o • ГПФ В DZ C 2 1 К 1 A 1 ФПГ 11 21 ГПГ C 1 1. Провести в плоскости АВС горизонталь и фронталь. 2. Из горизонтальной проекции точки S 1 провести прямую перпендикулярно к горизонтальной проекции горизонтали, а из фронтальной проекции точки S 2 – прямую перпендикулярно фронтальной проекции фронтали 3. Для нахождения точки К – точки пересечения этой прямой с заданной плоскостью АВС заключить указанную прямую во вспомогательную фронтально-проецирующую плоскость , строят линию пересечения плоскостей АВС и ; Найти точку К (К 1; К 2).