Лекция 5. Определение графа. Изоморфизм. Представление графов в

Лекция 5. Определение графа. Изоморфизм. Представление графов в ЭВМ.

Определение графа Графом G = называется пара множеств, где V- непустое, конечное множество элементов (вершины графа), а множество E – множество неупорядоченных пар элементов из V (рёбра графа). e = (a, b) = (b, a), где a и b вершины графа. Если две вершины соединены ребром, то эти вершины называются смежными. Число вершин |V| графа G называется порядком графа (Обозначение: Gn). Число рёбер |E|=m. Если число рёбер равно 0, то граф G − пустой (On).

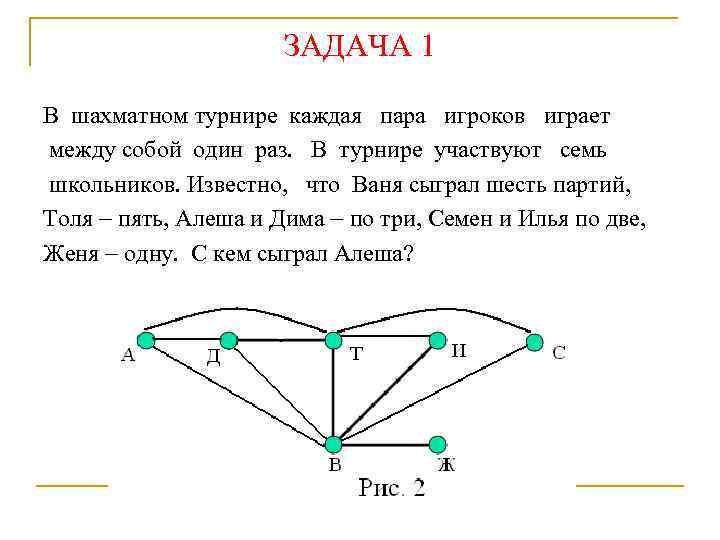ЗАДАЧА 1 В шахматном турнире каждая пара игроков играет между собой один раз. В турнире участвуют семь школьников. Известно, что Ваня сыграл шесть партий, Толя пять, Алеша и Дима по три, Семен и Илья по две, Женя одну. С кем сыграл Алеша?

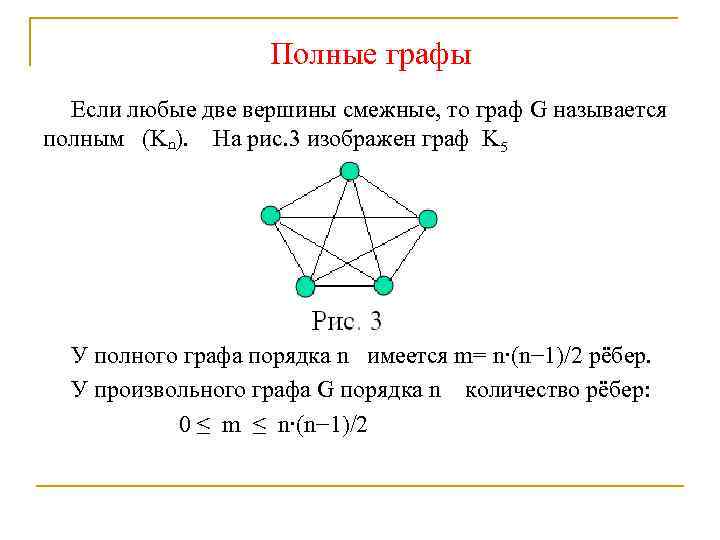Полные графы Если любые две вершины смежные, то граф G называется полным (Kn). На рис. 3 изображен граф K 5 У полного графа порядка n имеется m= n∙(n− 1)/2 рёбер. У произвольного графа G порядка n количество рёбер: 0 ≤ m ≤ n∙(n− 1)/2

ЗАДАЧА 2 Чемпионат детского лагеря по футболу проводился по круговой системе. За победу в матче давалось 2 очка, за ничью 1, за поражение 0. Если две команды набирали одинаковое количество очков, то место определялось по разности забитых и пропущенных мячей. Чемпион набрал 7 очков, второй призер 5, третий 3 очка. Сколько очков набрала команда, занявшая последнее место?

Таблица распределения мест Пусть было n команд. В графе будет n (n-1)/2 ребер. Разыграно n (n-1) очков. На долю трех призеров приходится 15 очков. Остальные команды набрали не более 3 (n-3) очков. Поэтому n (n 1) – 15<= 3 (n 3), (n 2)2 <=11, n<=5. При n=4 n(n-1)=12<15. Значит, n = 5.

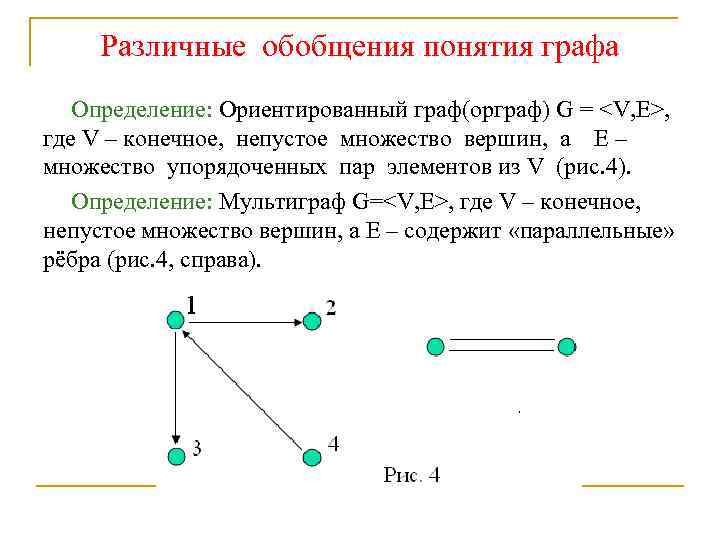Различные обобщения понятия графа Определение: Ориентированный граф(орграф) G = , где V – конечное, непустое множество вершин, а Е – множество упорядоченных пар элементов из V (рис. 4). Определение: Мультиграф G=, где V – конечное, непустое множество вершин, а Е – содержит «параллельные» рёбра (рис. 4, справа).

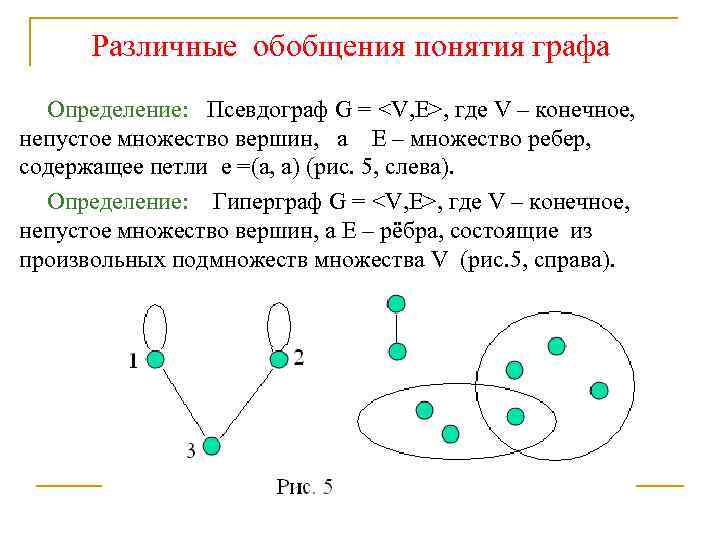Различные обобщения понятия графа Определение: Псевдограф G = , где V – конечное, непустое множество вершин, а Е – множество ребер, содержащее петли e =(a, a) (рис. 5, слева). Определение: Гиперграф G = , где V – конечное, непустое множество вершин, а Е – рёбра, состоящие из произвольных подмножества V (рис. 5, справа).

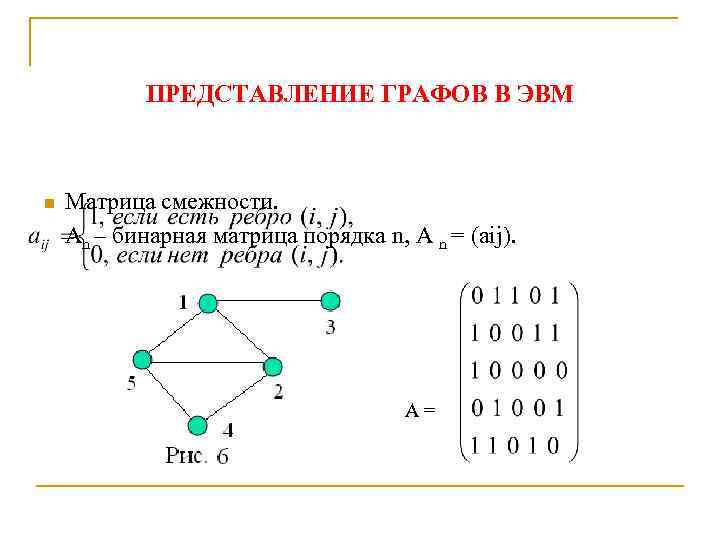ПРЕДСТАВЛЕНИЕ ГРАФОВ В ЭВМ n Матрица смежности. Аn – бинарная матрица порядка n, А n = (аij). A=

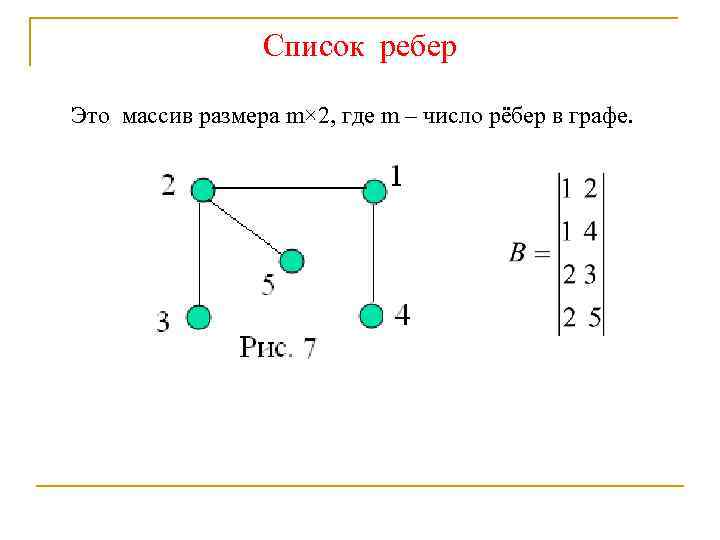Список ребер Это массив размера m× 2, где m – число рёбер в графе.

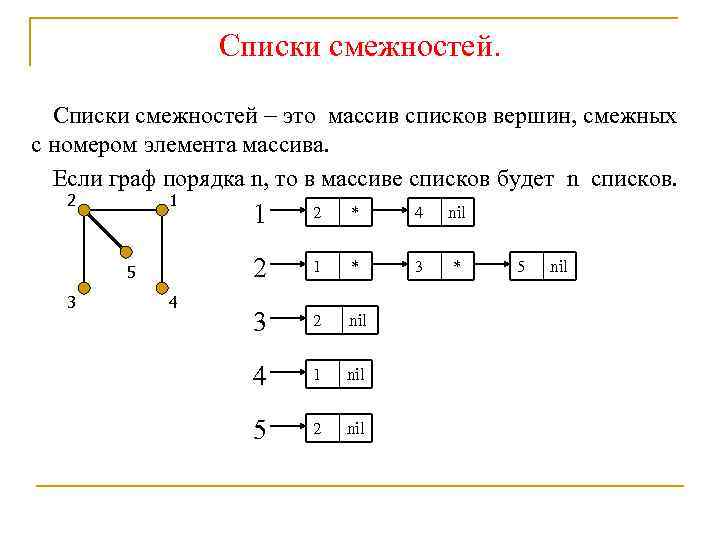Списки смежностей это массив списков вершин, смежных с номером элемента массива. Если граф порядка n, то в массиве списков будет n списков. 2 1 3 4 2 * 4 nil 2 5 1 1 * 3 2 nil 4 1 nil 5 2 nil 5 nil

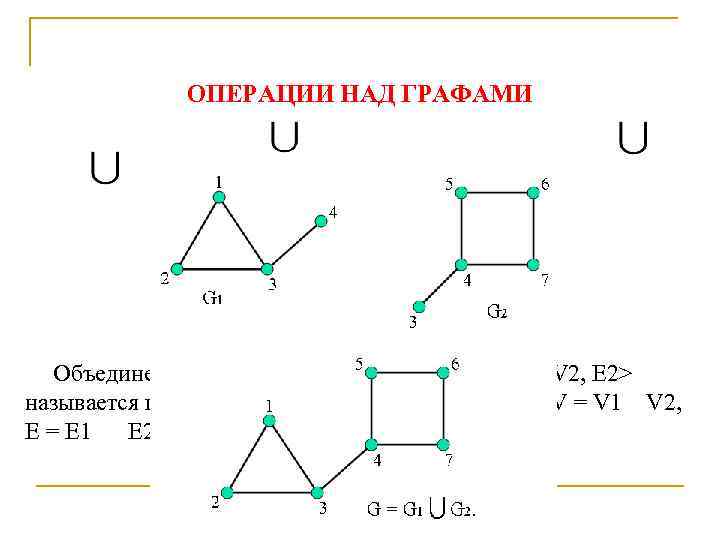ОПЕРАЦИИ НАД ГРАФАМИ Объединением графов G 1= и G 2= называется граф G = G 1 G 2, где G = , и V = V 1 V 2, E = E 1 E 2.

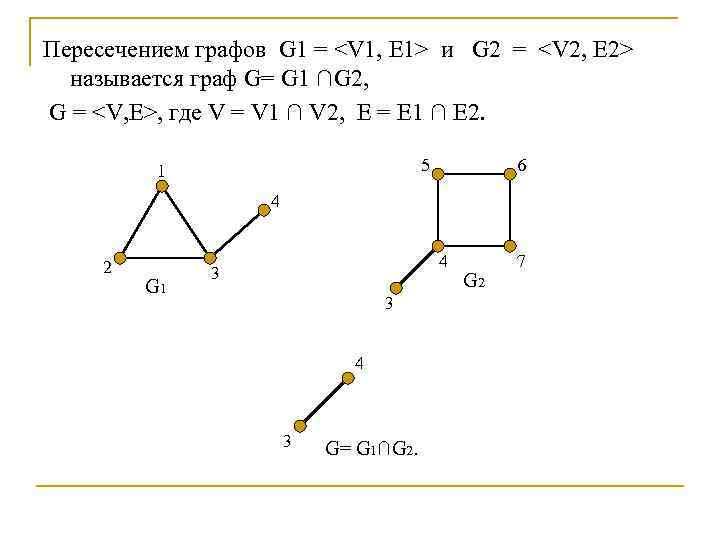Пересечением графов G 1 = и G 2 = называется граф G= G 1 ∩G 2, G = , где V = V 1 ∩ V 2, E = E 1 ∩ E 2. 5 1 6 4 2 G 1 4 3 3 4 3 G= G 1∩G 2. G 2 7

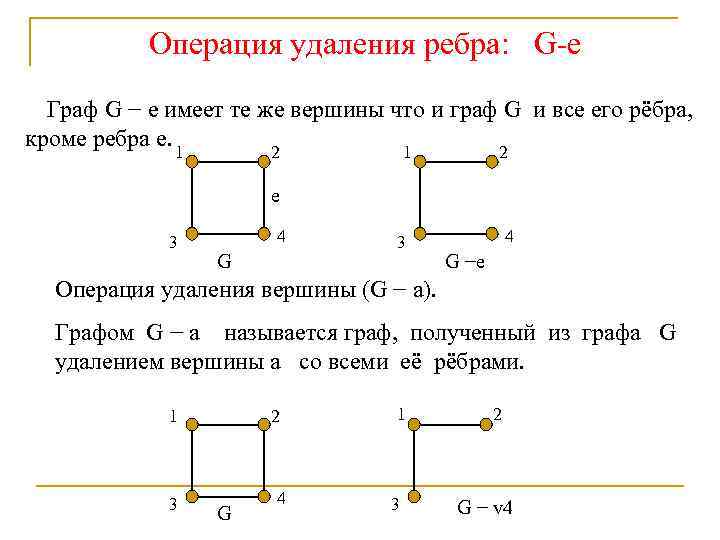Операция удаления ребра: G-e Граф G − e имеет те же вершины что и граф G и все его рёбра, кроме ребра е. 1 2 e 3 4 G −e Операция удаления вершины (G − а). Графом G − а называется граф, полученный из графа G удалением вершины а со всеми её рёбрами. 1 3 2 G 4 1 3 2 G − v 4

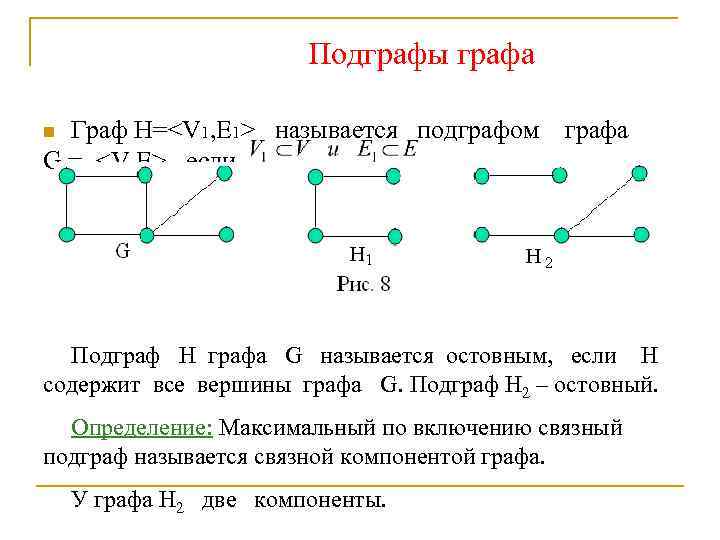Подграфы графа Граф Н= называется подграфом G = , если. n графа Подграф Н графа G называется остовным, если Н содержит все вершины графа G. Подграф Н 2 – остовный. Определение: Максимальный по включению связный подграф называется связной компонентой графа. У графа Н 2 две компоненты.

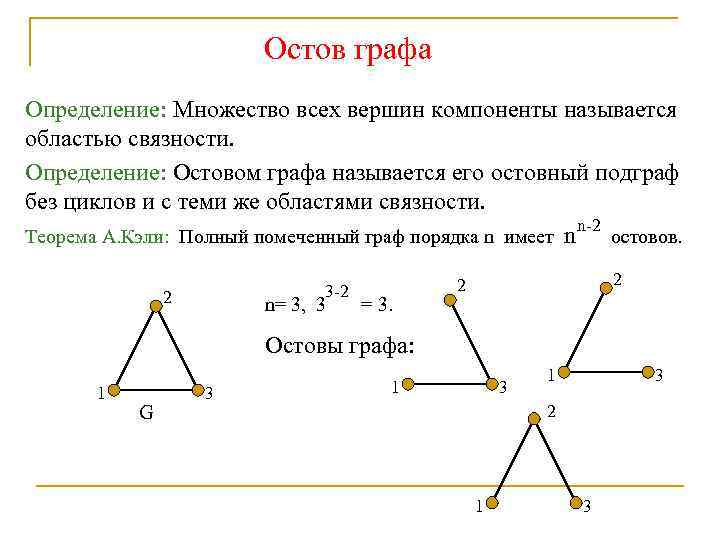Остов графа Определение: Множество всех вершин компоненты называется областью связности. Определение: Остовом графа называется его остовный подграф без циклов и с теми же областями связности. n-2 Теорема А. Кэли: Полный помеченный граф порядка n имеет n остовов. 3 -2 2 n= 3, 3 = 3. 2 2 Остовы графа: 1 G 3 1 3 2 1 3

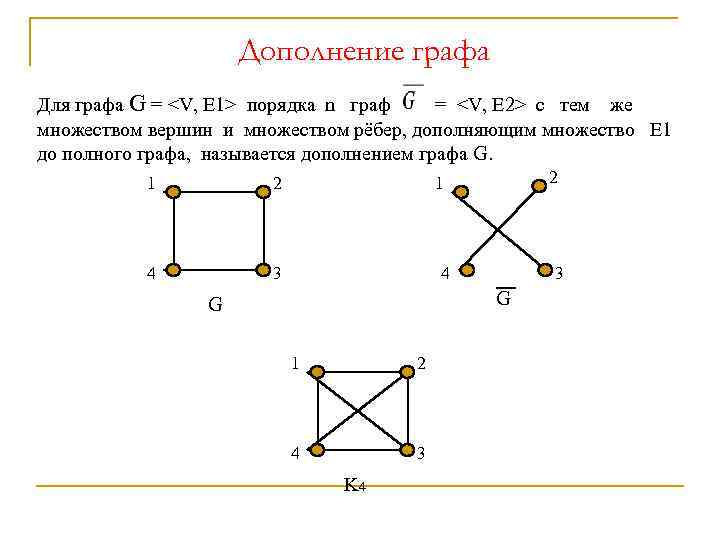Дополнение графа Для графа G = порядка n граф = с тем же множеством вершин и множеством рёбер, дополняющим множество E 1 до полного графа, называется дополнением графа G. 1 2 4 3 2 1 4 3 G G 1 2 4 3 K 4

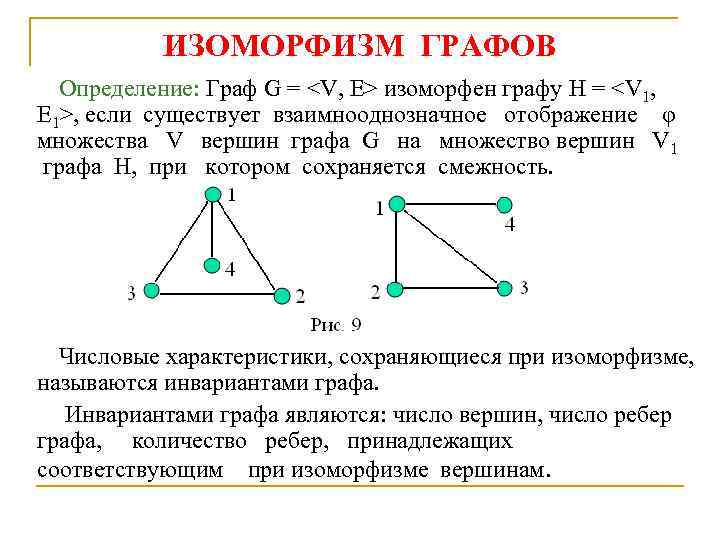ИЗОМОРФИЗМ ГРАФОВ Определение: Граф G = изоморфен графу H = , если существует взаимнооднозначное отображение φ множества V вершин графа G на множество вершин V 1 графа H, при котором сохраняется смежность. Числовые характеристики, сохраняющиеся при изоморфизме, называются инвариантами графа. Инвариантами графа являются: число вершин, число ребер графа, количество ребер, принадлежащих соответствующим при изоморфизме вершинам.

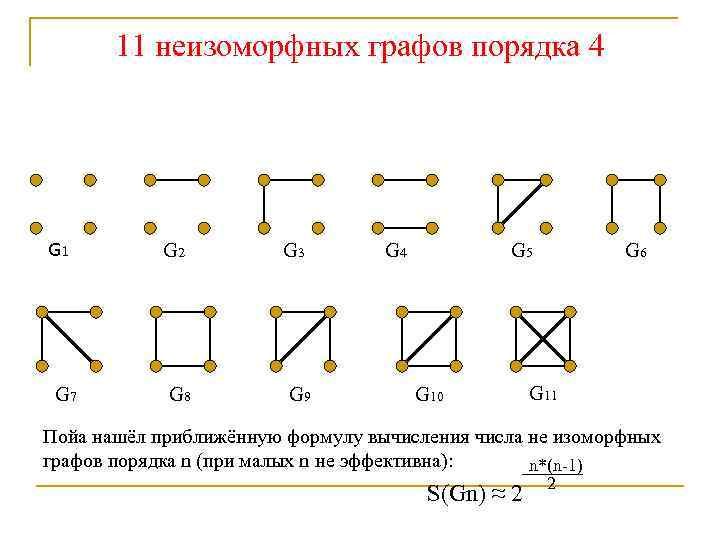11 неизоморфных графов порядка 4 G 1 G 7 G 2 G 3 G 8 G 9 G 4 G 5 G 10 G 6 G 11 Пойа нашёл приближённую формулу вычисления числа не изоморфных графов порядка n (при малых n не эффективна): n*(n-1) S(Gn) ≈ 2 2