Лекция 5 Методы расчета и анализа электрических цепей

Лекция 5 Методы расчета и анализа электрических цепей

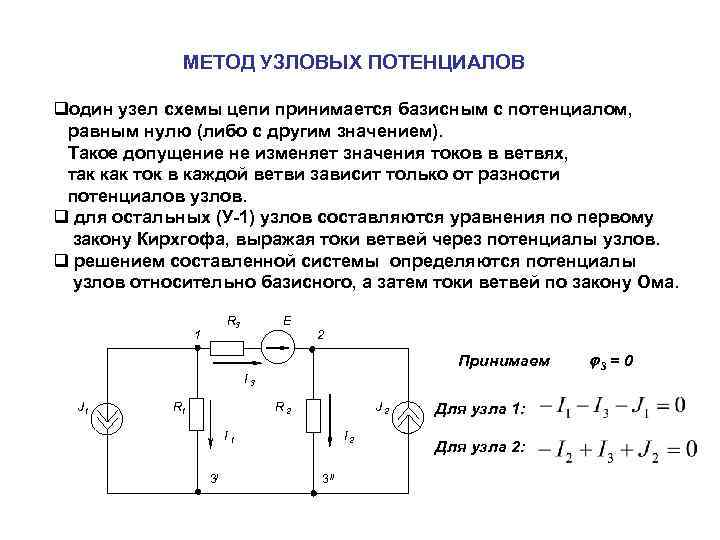МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ qодин узел схемы цепи принимается базисным с потенциалом, равным нулю (либо с другим значением). Такое допущение не изменяет значения токов в ветвях, так как ток в каждой ветви зависит только от разности потенциалов узлов. q для остальных (У-1) узлов составляются уравнения по первому закону Кирхгофа, выражая токи ветвей через потенциалы узлов. q решением составленной системы определяются потенциалы узлов относительно базисного, а затем токи ветвей по закону Ома. 1 R 3 E 2 Принимаем I 3 J 1 R 2 I 1 3/ 3 // J 2 I 2 Для узла 1: Для узла 2: 3 = 0

После подстановки в уравнения токов:

Метод узловых потенциалов • Метод в котором за неизвестные принимают потенциалы узлов схемы • Составляют Nуп = m – 1, так как один узел в схеме можно заземлить, то есть принять его потенциал равным нулю без изменения тока распределения в схеме

Метод узловых потенциалов • Если схема имеет в своем составе(у+1) узел, а потенциал у+1 узла равен нулю, для определения потенциалов ост узлов необходимо составить у уравнений • ϕ 1 g 11 -ϕ 2 g 12 -ϕ 3 g 13 -…ϕyg 1 y=∑J+∑Eg • -ϕ 1 g 21+ϕ 2 g 22 -ϕ 3 g 23 -…ϕyg 2 y=∑J+∑Eg • -ϕ 1 g 31 -ϕ 2 g 22+ϕ 3 g 33 -…ϕyg 3 y=∑J+∑Eg • -ϕ 1 gy 1 -ϕ 2 gy 2 -ϕ 3 g 33 -…+ϕygyy=∑J+∑Eg

Метод узловых потенциалов • Gnn -сумма проводимостей ветвей, присоединенных к узлу n (Gnn = 1/Rnn) • Gkm=Gmk – сумма проводимостей ветвей, соединяющих k и m узлы (Gkm = 1/Rmk) • ∑J – сумма токов источников тока присоединенных к узлу k (+ от узла, -к узлу) • ∑Eg – сумма произведений ЭДС источника на проводимость для каждой ветви узла (+ от узла, -к узлу)

Метод узловых потенциалов • Если в схеме есть узлы соединенные через идеальный источник ЭДС, то число уравнений сокращается m-Nвиэ-1 • m- число узлов • Nвиэ- число ветвей с идеальным источником ЭДС • Рекомендуется принять равным нулю потенциал узла к которой подходит ЭДС

Метод узловых потенциалов • Составляем систему из k=m-Nвит-1 • Решаем систему относительно потенциалов узлов • Находим токи в ветвях по закону Ома ток в ветви с идеальным источником ЭДС находится в последнюю очередь по первому закону Кирхгофа

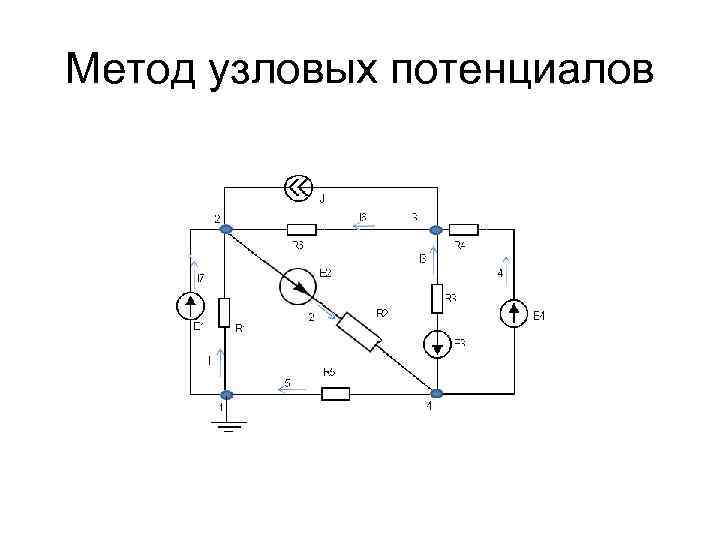Метод узловых потенциалов

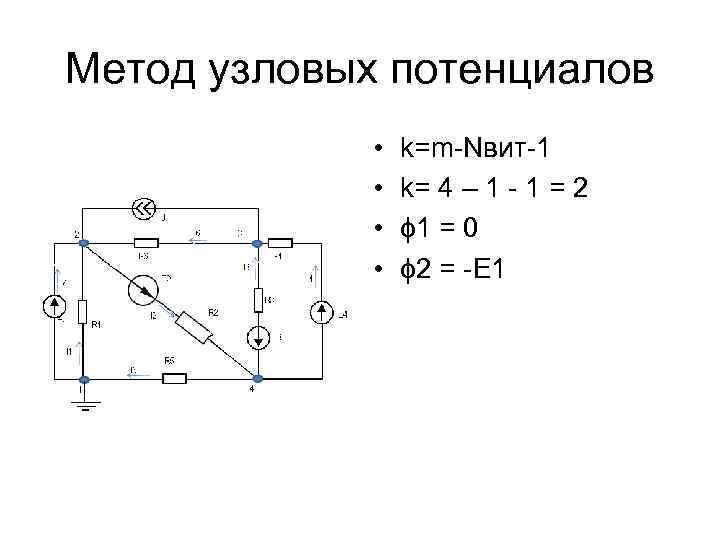Метод узловых потенциалов • • k=m-Nвит-1 k= 4 – 1 - 1 = 2 ϕ 1 = 0 ϕ 2 = -E 1

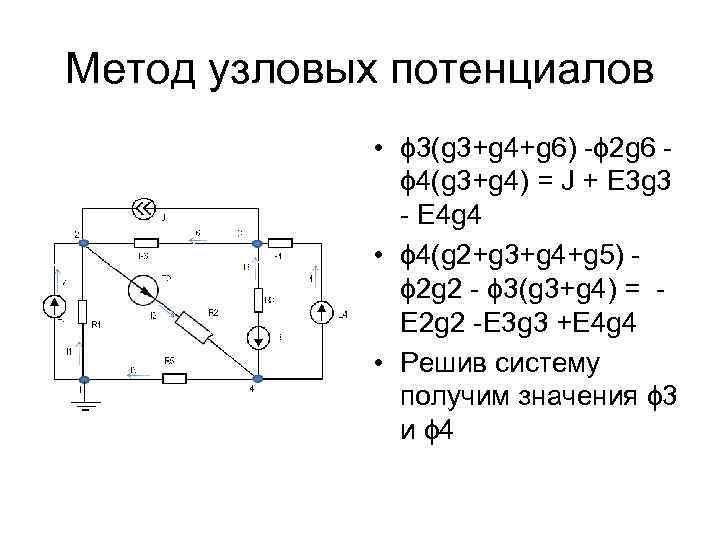Метод узловых потенциалов • ϕ 3(g 3+g 4+g 6) -ϕ 2 g 6 - ϕ 4(g 3+g 4) = J + E 3 g 3 - E 4 g 4 • ϕ 4(g 2+g 3+g 4+g 5) ϕ 2 g 2 - ϕ 3(g 3+g 4) = E 2 g 2 -E 3 g 3 +E 4 g 4 • Решив систему получим значения ϕ 3 и ϕ 4

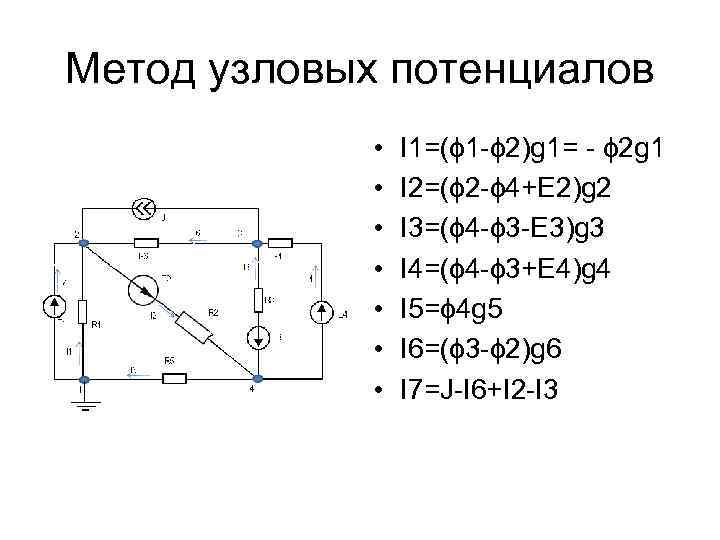Метод узловых потенциалов • • I 1=(ϕ 1 -ϕ 2)g 1= - ϕ 2 g 1 I 2=(ϕ 2 -ϕ 4+E 2)g 2 I 3=(ϕ 4 -ϕ 3 -E 3)g 3 I 4=(ϕ 4 -ϕ 3+E 4)g 4 I 5=ϕ 4 g 5 I 6=(ϕ 3 -ϕ 2)g 6 I 7=J-I 6+I 2 -I 3

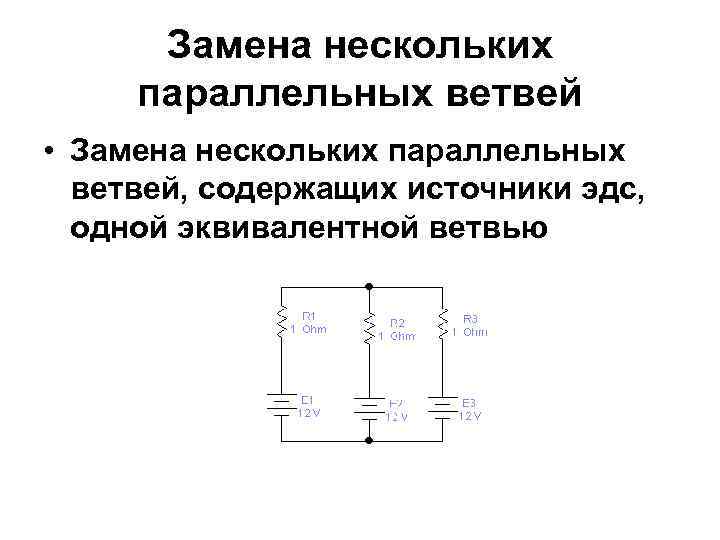Замена нескольких параллельных ветвей • Замена нескольких параллельных ветвей, содержащих источники эдс, одной эквивалентной ветвью

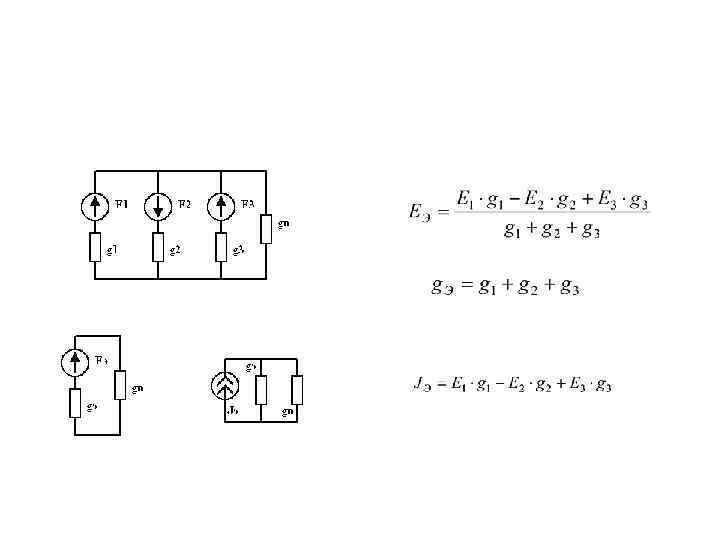
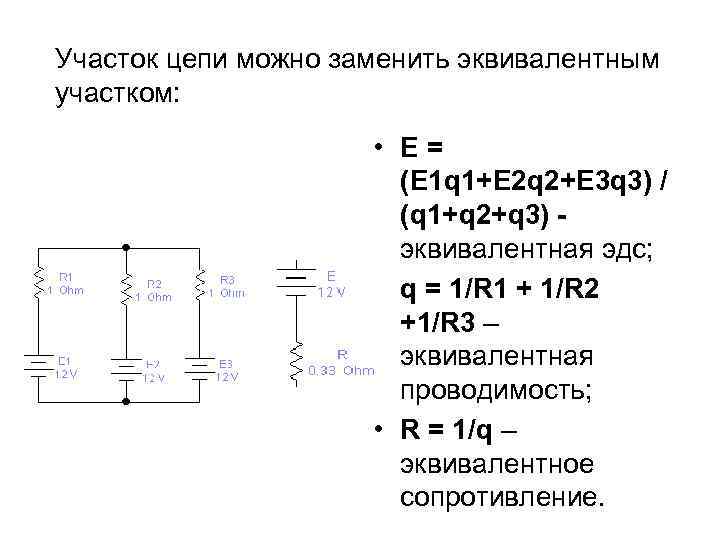Участок цепи можно заменить эквивалентным участком: • Е= (Е 1 q 1+Е 2 q 2+Е 3 q 3) / (q 1+q 2+q 3) эквивалентная эдс; • q = 1/R 1 + 1/R 2 +1/R 3 – эквивалентная проводимость; • R = 1/q – эквивалентное сопротивление.

Замена нескольких параллельных ветвей • Если в какой либо ветви эдс отсутствует, то соответствующее слагаемое в числителе выпадает, но проводимость этой ветви в знаменателе будет присутствовать. Если эдс в схеме имеет направление, обратное изображенному направлению эдс на рисунке, то соответствующее слагаемое войдет в числитель со знаком минус.

• Часть схемы, состоящей из параллельных ветвей ЭДС и проводимостями , эквивалентно либо одной ветви с проводимостью и ЭДС : • , • либо двум параллельным ветвям с той же проводимостью и источником тока : • • .

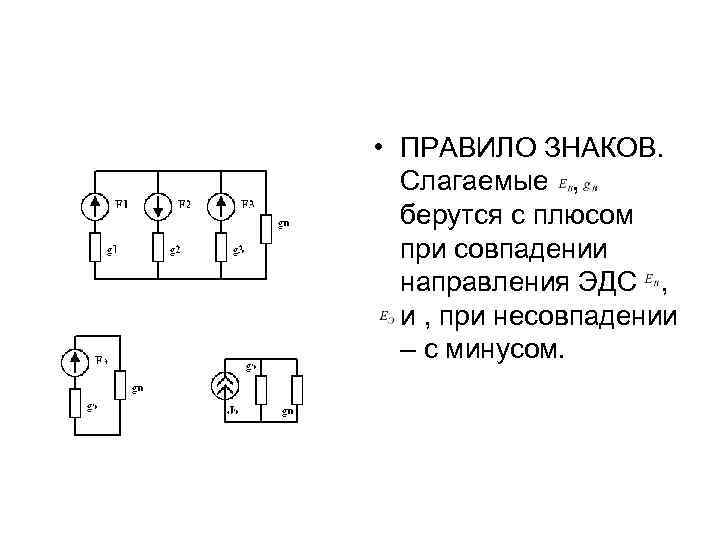• ПРАВИЛО ЗНАКОВ. Слагаемые , берутся с плюсом при совпадении направления ЭДС , и , при несовпадении – с минусом.

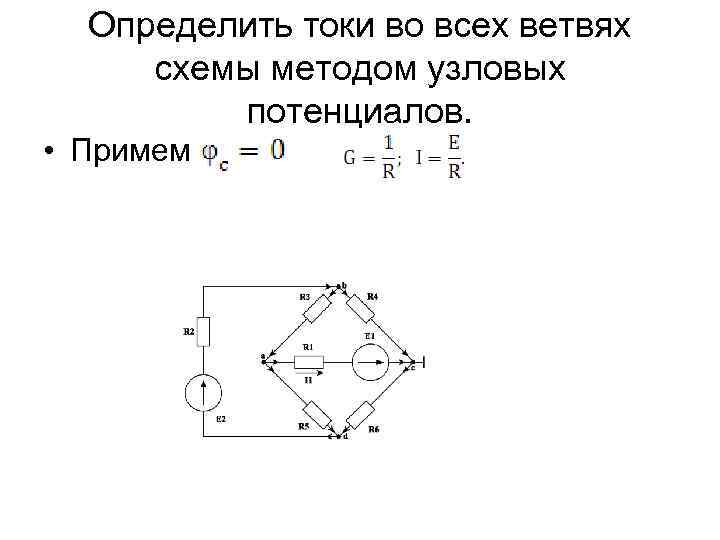Определить токи во всех ветвях схемы методом узловых потенциалов. • Примем

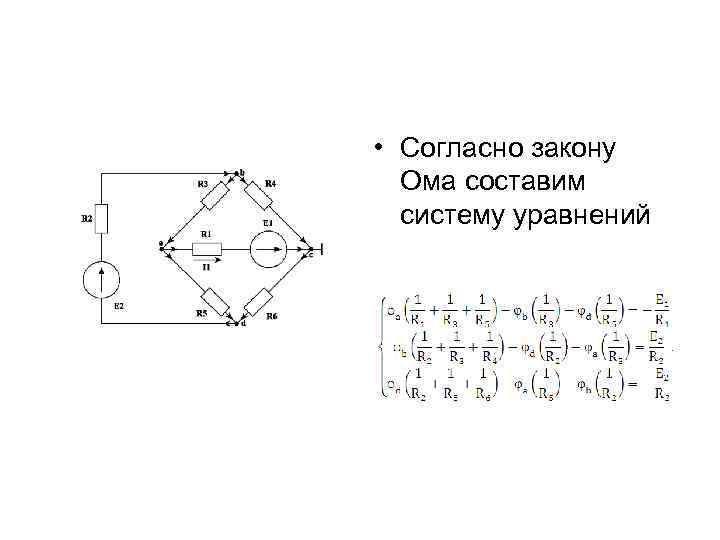• Согласно закону Ома составим систему уравнений

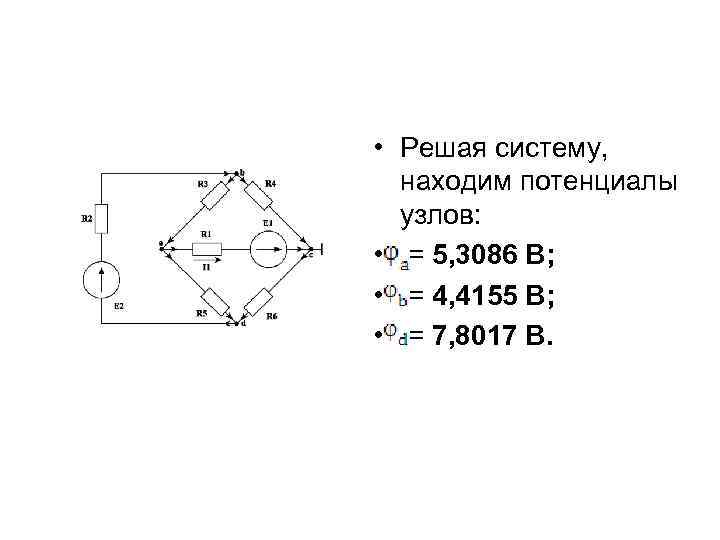• Решая систему, находим потенциалы узлов: • = 5, 3086 В; • = 4, 4155 В; • = 7, 8017 В.

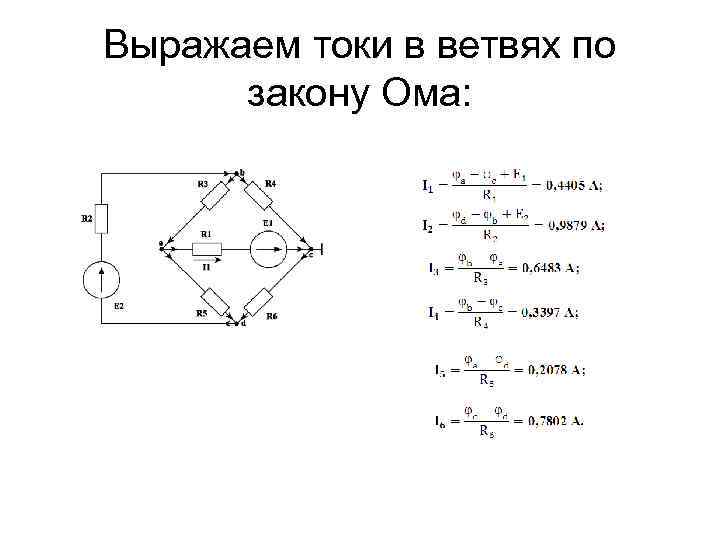Выражаем токи в ветвях по закону Ома:

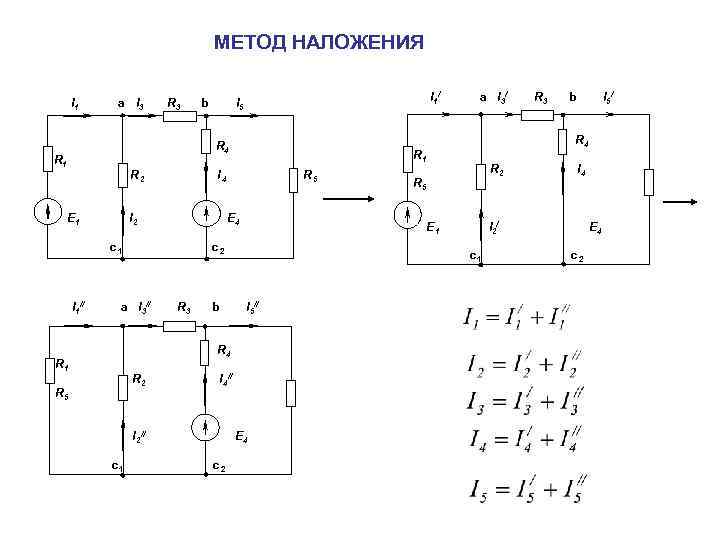МЕТОД НАЛОЖЕНИЯ I 1 a I 3 R 3 b I 1/ I 5 R 4 R 1 R 2 E 1 E 4 c 1 I 1// R 5 a I 3// R 3 b I 5// R 2 R 5 I 4// I 2// c 1 E 4 c 2 b I 5/ I 4 I 2/ c 1 R 4 R 1 R 2 R 5 E 1 c 2 R 3 R 4 R 1 I 4 I 2 a I 3/ E 4 c 2

МЕТОД ДВУХ УЗЛОВ a 1 a 2 По первому закону Кирхгофа R 1 R 3 R 2 E 1 R 4 E 3 b 1 b 2 Знак Uab обусловлен уравнением:

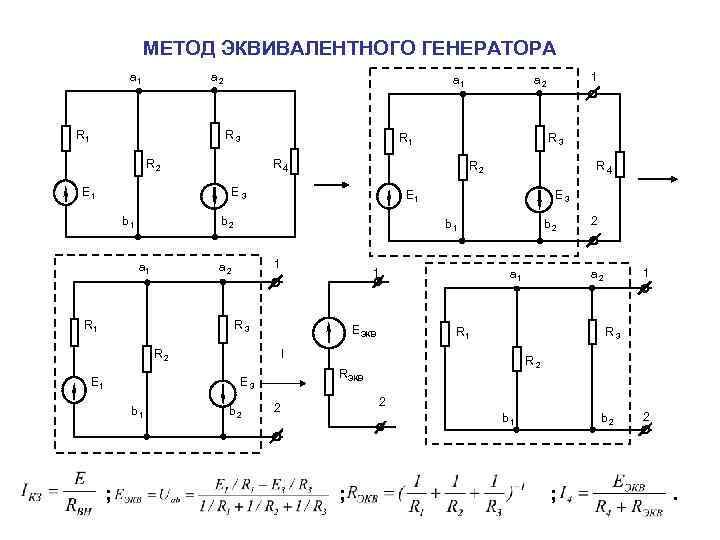МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА 1 a 2 a 1 a 2 R 1 R 3 R 2 R 4 E 1 E 3 b 1 b 2 a 1 a 2 1 a 2 E ЭКВ R 1 R 3 RЭКВ E 1 E 3 ; 2 1 R 1 R 3 R 2 R 4 b 1 b 2 2 2 ; R 2 R 4 b 1 b 2 ; 2 .

Метод ЭГ • Определить ток I 1 в заданной по условию схеме, используя теорему об активном двухполюснике и эквивалентном генераторе. • Выделим из схемы ветвь, в которой необходимо определить ток:

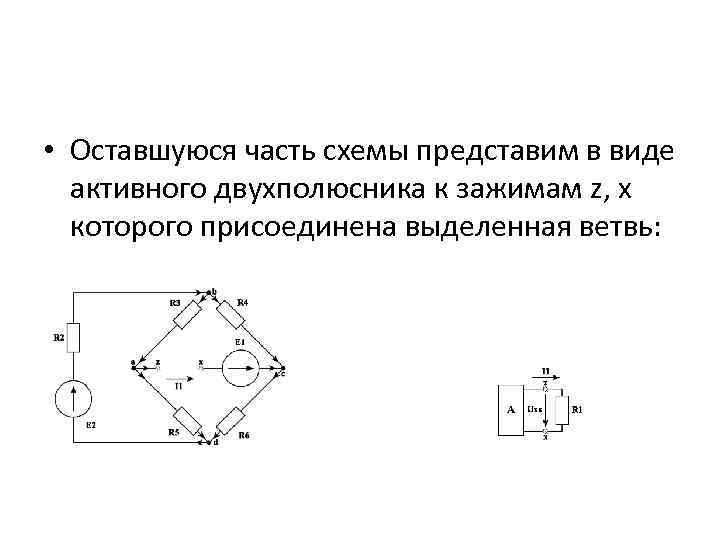• Оставшуюся часть схемы представим в виде активного двухполюсника к зажимам z, x которого присоединена выделенная ветвь:

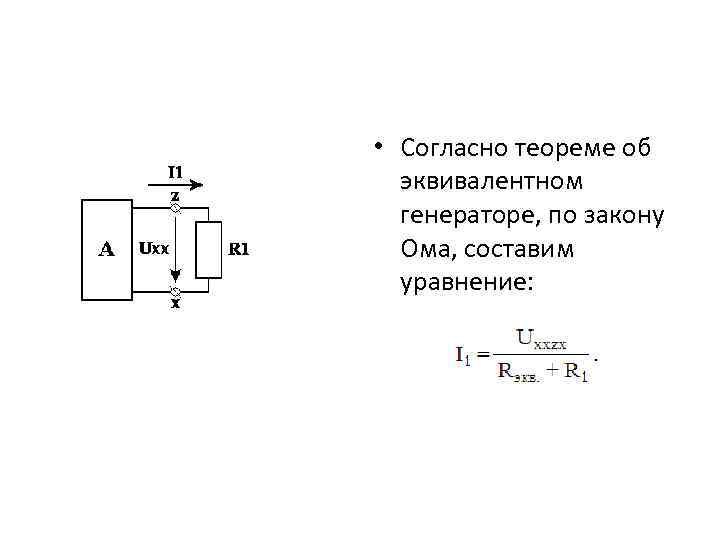• Согласно теореме об эквивалентном генераторе, по закону Ома, составим уравнение:

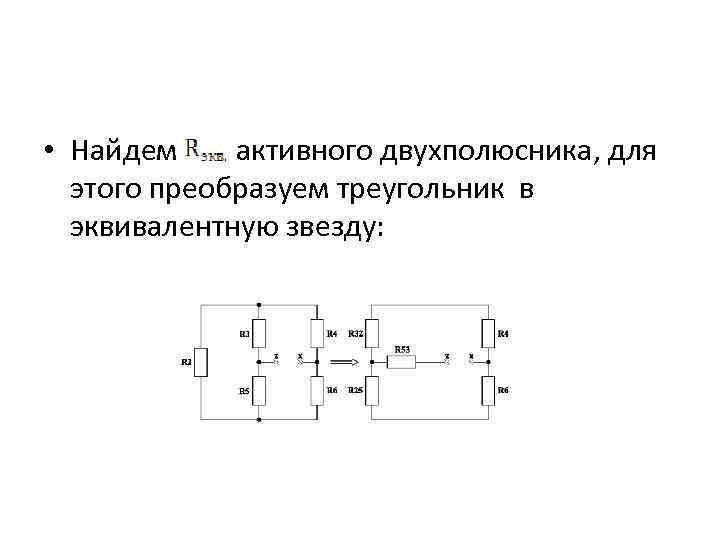• Найдем активного двухполюсника, для этого преобразуем треугольник в эквивалентную звезду:

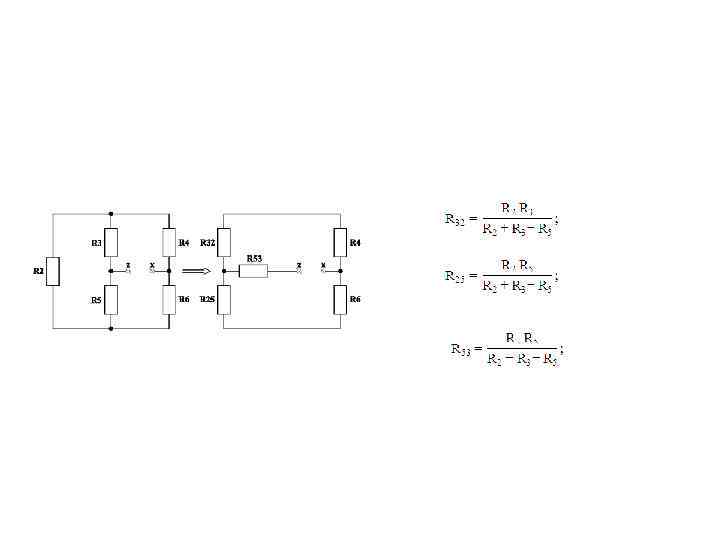
• • • 6 Ом; 4, 8 Ом; 4 Ом;

; ; ; • Найдем активного двухполюсника методом узловых потенциалов:

• = 4, 3575 В; = 14, 9575 В • Найдем ток I 1: • I 1 = 0, 4358 А.