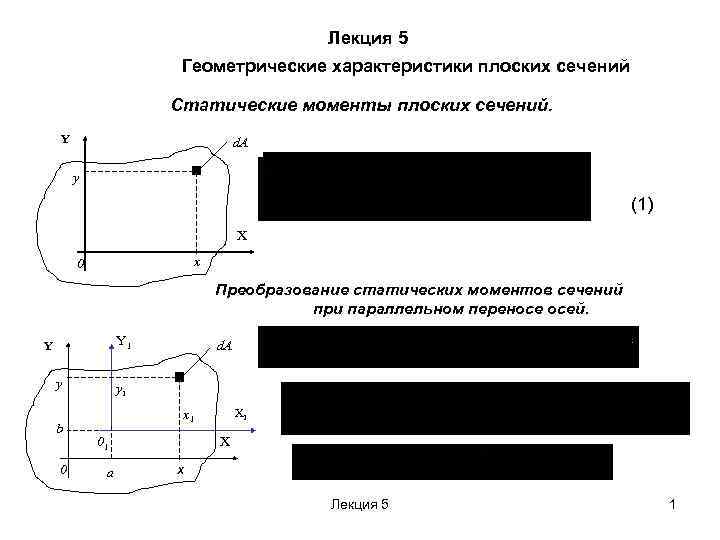
Лекция 5 Геометрические характеристики плоских сечений Статические моменты

Лекция 5 Геометрические характеристики плоских сечений Статические моменты плоских сечений. Y d. A y см 3, м 3 (1) X x 0 Преобразование статических моментов сечений при параллельном переносе осей. Y 1 Y y b 0 d. A y 1 X 1 x 1 01 a X xx Лекция 5 1

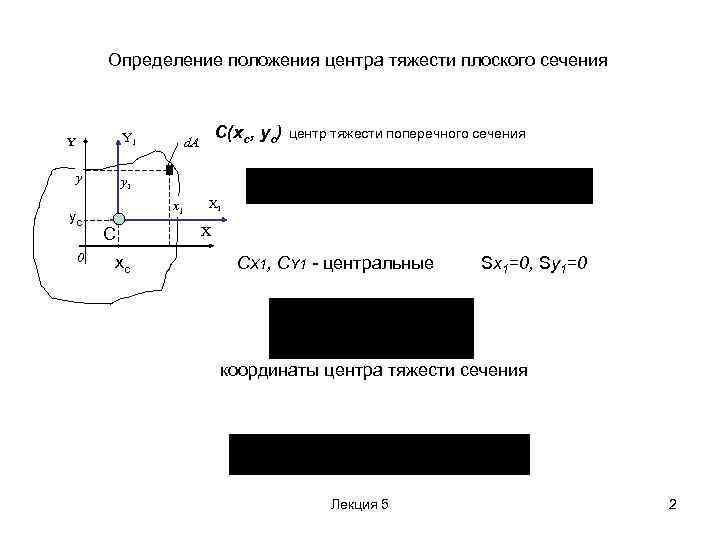Определение положения центра тяжести плоского сечения Y 1 Y y yc 0 С(xc, yc) центр тяжести поперечного сечения d. A y 1 x 1 X C xc X 1 x СХ 1, СY 1 - центральные Sx 1=0, Sy 1=0 координаты центра тяжести сечения Лекция 5 2

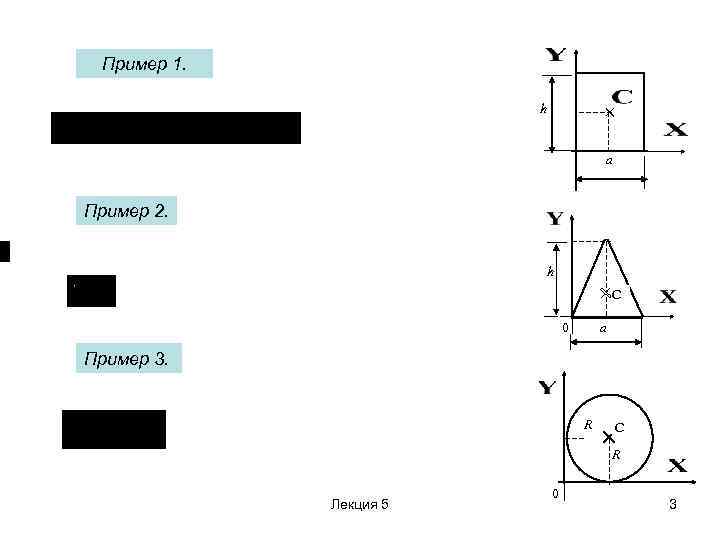Пример 1. h a Пример 2. h С a 0 Пример 3. R С R Лекция 5 0 3

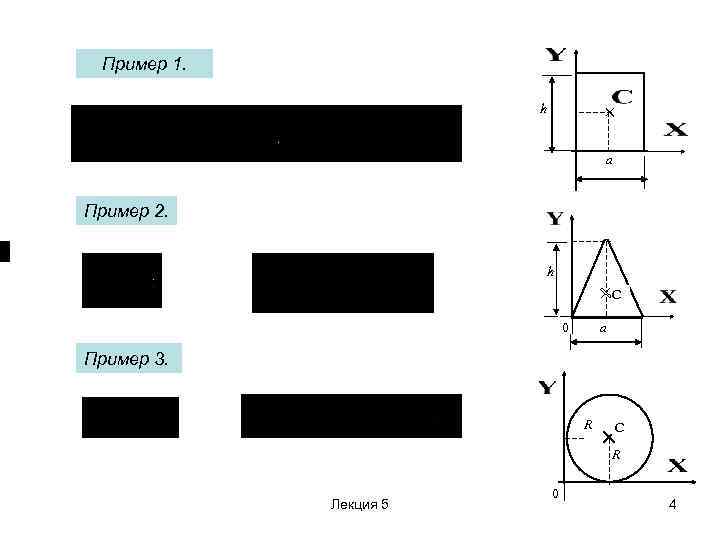Пример 1. h a Пример 2. h С a 0 Пример 3. R С R Лекция 5 0 4

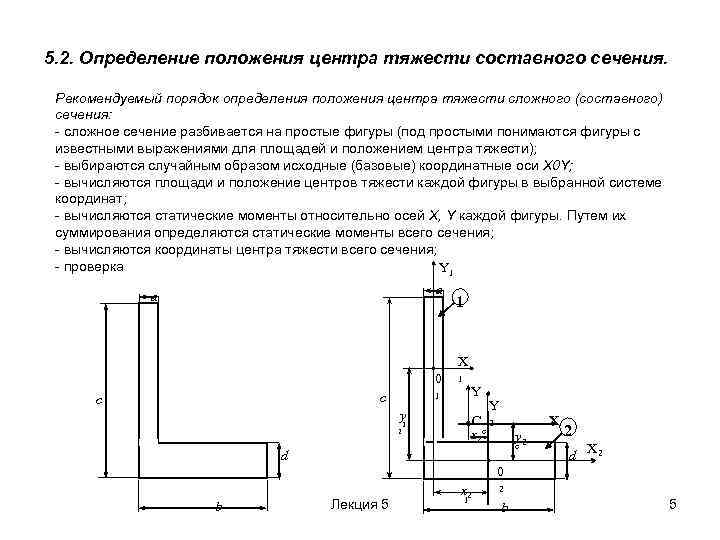5. 2. Определение положения центра тяжести составного сечения. Рекомендуемый порядок определения положения центра тяжести сложного (составного) сечения: - сложное сечение разбивается на простые фигуры (под простыми понимаются фигуры с известными выражениями для площадей и положением центра тяжести); - выбираются случайным образом исходные (базовые) координатные оси X 0 Y; - вычисляются площади и положение центров тяжести каждой фигуры в выбранной системе координат; - вычисляются статические моменты относительно осей X, Y каждой фигуры. Путем их суммирования определяются статические моменты всего сечения; - вычисляются координаты центра тяжести всего сечения; - проверка Y 1 a a 1 X 0 c c 1 Y 1 y 2 Y X C 2 x 2 c 1 y 2 c d 2 d X 2 0 b Лекция 5 x 2 1 2 b 5

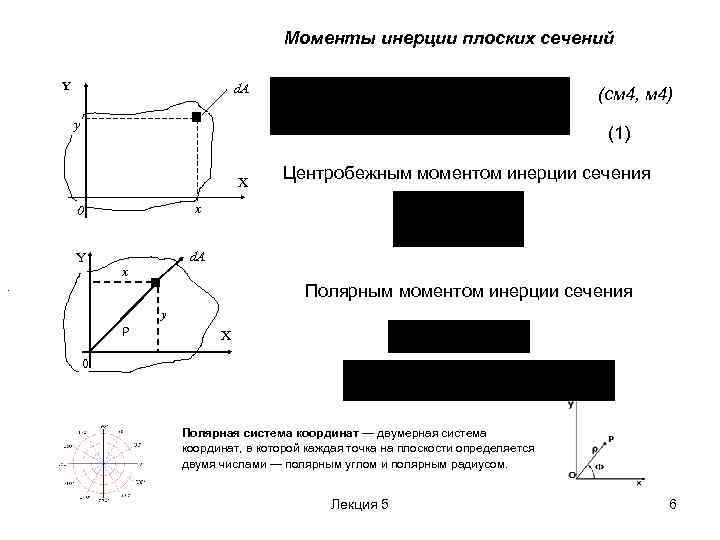Моменты инерции плоских сечений Y d. A (см 4, м 4) y (1) X 0 . x Y Центробежным моментом инерции сечения d. A x Полярным моментом инерции сечения y X 0 Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Лекция 5 6

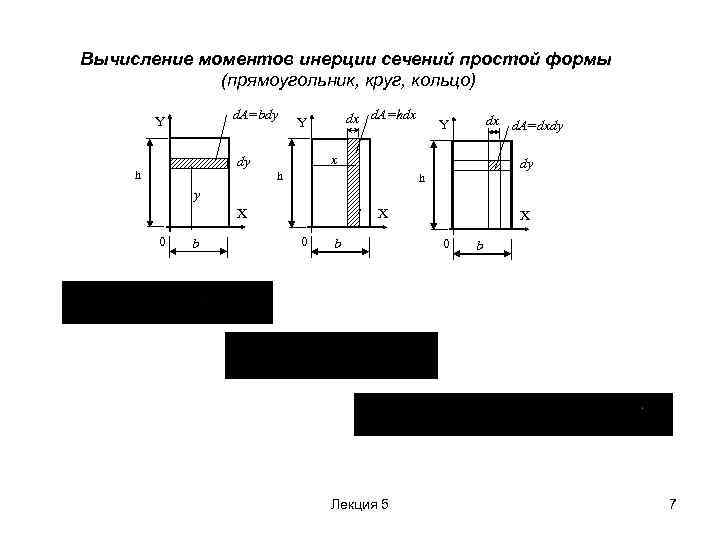Вычисление моментов инерции сечений простой формы (прямоугольник, круг, кольцо) d. A=bdy Y dy h dx d. A=hdx Y x h , X b dy h y 0 dx d. A=dxdy Y 0 X b X 0 b Лекция 5 7

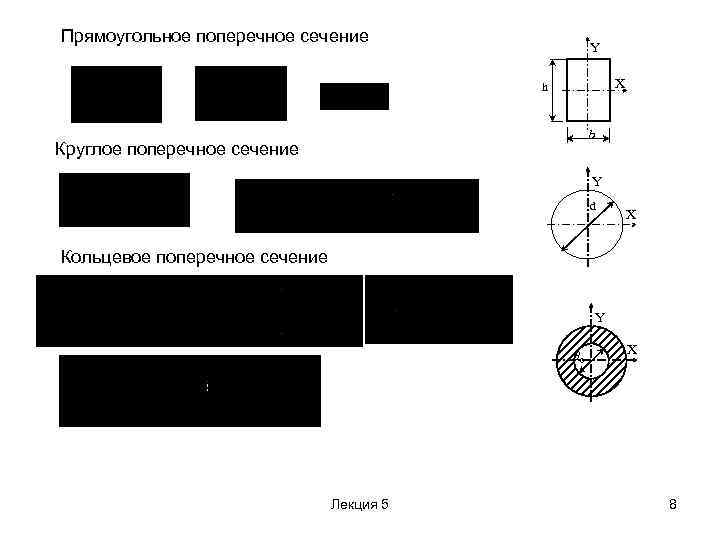Прямоугольное поперечное сечение Y X h b Круглое поперечное сечение Y d X Кольцевое поперечное сечение Y d 0 Лекция 5 X 8

Преобразование моментов инерции при параллельном переносе осей Y 1 Y y b 0 d. A y 1 x 1 01 a X 1 X x Если исходные оси X 0 Y являются центральными, то Sx=0, Sy=0. Лекция 5 9

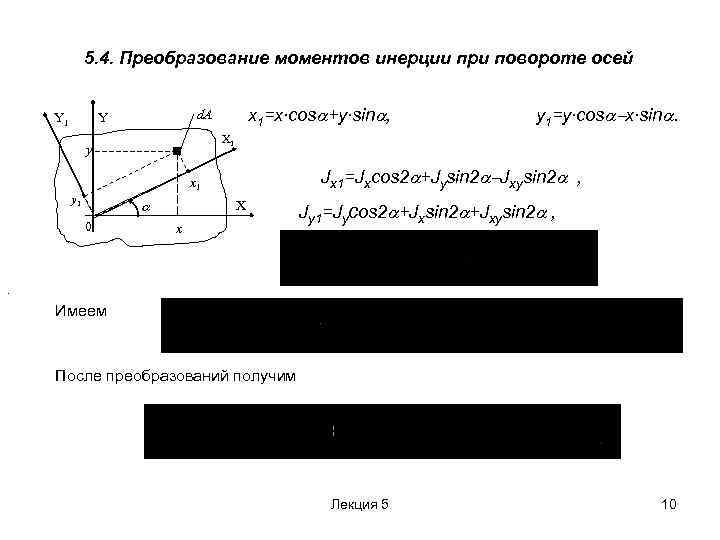5. 4. Преобразование моментов инерции при повороте осей Y 1 Jx 1=Jxcos 2 +Jysin 2 Jxysin 2 , x 1 y 1 0 y 1=y∙cos x∙sin. X 1 y . x 1=x∙cos +y∙sin , d. A Y X x Jy 1=Jycos 2 +Jxsin 2 +Jxysin 2 , Имеем . После преобразований получим Лекция 5 10

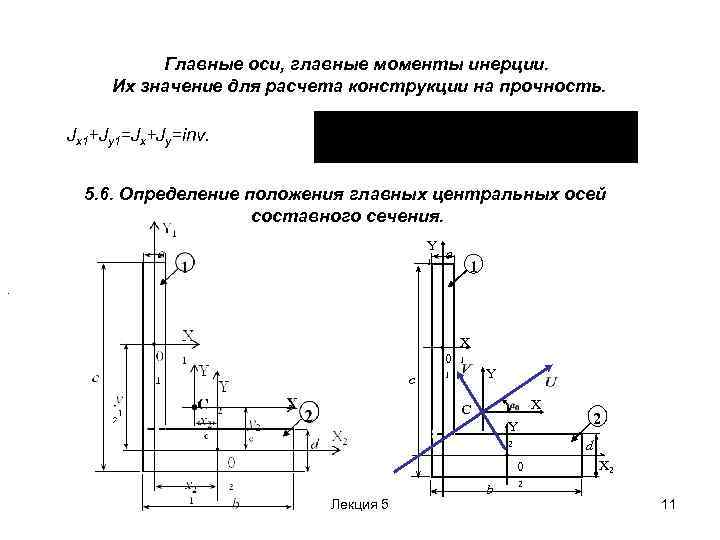Главные оси, главные моменты инерции. Их значение для расчета конструкции на прочность. Jx 1+Jy 1=Jx+Jy=inv. 5. 6. Определение положения главных центральных осей составного сечения. Y 1 a 1 . X 0 c 1 Y 1 X C 2 Y d 2 0 Лекция 5 b X 2 2 11