ЛЕКЦИЯ 5 ФЕРРОМАГНЕТИКИ ФЕРРОМАГНЕТИКИ Ферромагнетики

ЛЕКЦИЯ 5

ФЕРРОМАГНЕТИКИ

ФЕРРОМАГНЕТИКИ Ферромагнетики – твердые вещества, обладающие при не слишком высоких температурах самопроизвольной намагниченностью, которая сильно изменяется под влиянием внешних воздействий (магнитного поля, деформации, изменения температуры). Ферромагнетики –сильномагнитные вещества, внутреннее магнитное поле в них может в сотни и тысячи раз превосходить внешнее. Примеры ферромагнетиков: железо, кобальт, никель, некоторые сплавы.

СВОЙСТВА ФЕРРОМАГНЕТИКОВ На рисунке показана зависимость намагниченности от напряжен. Ферро. Параности магнитного поля. По мемагнетик ре возрастания , растет сначала быстро, затем медленнее, и диамагнетик при достижении значения модуль вектора намагниченности не зависит от напряженности внешнего поля, остается постоянным и равен. Данный эффект называется магнитным насыщением. По мере увеличения намагничивающего поля, увеличивается степень ориентации молекулярных магнитных моментов по полю, но этот процесс начнет замедляться, когда остается все меньше и меньше неориентированных моментов, и когда все моменты будут ориентированы по полю,

увеличение прекращается, и наступает магнитное насыщение. На рисунке показана зависимость вектора магнитной индукции от. График отличается от отсутствием «горизонтальной» части. Как только наступит насыщение, магнитная индукция увеличивается по линейному закону, в зависимости от напряженности маг нитного поля. Характерная особенность ферромагнетиков – большое значение магнитной проницаемости (для железа. , максимальные значения для некоторых сплавов ).

На рисунке показана зависимость магнитной проницаемости от. Сначала быстро растет, а затем быстро 1 убывает стремясь к единице в очень сильных намагничивающих полях. Это объясняется тем, что при очень больших значениях в формуле можно пренебречь по сравнению с , тогда. Зависимость от существенно зависит от того, каким предварительным воздействиям подвергался ферромагнетик. Ферромагнетик обладает свойством частичного сохранения намагниченности после удаления из внешнего магнитного поля. это связано с наличием у магнетика МАГНИТНОГО ГИСТЕРЕЗИСА (запаздывания).

МАГНИТНЫЙ ГИСТЕРЕЗИС Если размагниченный ферро 1 магнетик (точка 0) намагнитить до насыщения (1), а затем ум 2 еньшать напряженность , то 6 уменьшение описывается кри 3 5 вой 1 -2 , лежащей выше ис4 ходной 0 -1. При отличается от нуля, то есть в ферромагнетике наблюдается остаточное намагничивание. С наличием остаточного намагничивания связано существование постоянных магнитов. Намагничивание обращается в нуль под действием поля , имеющего направление противоположное полю, вызвавшего намагничивание, и напряженность называется – коэрцитивная сила.

При дальнейшем увеличении противоположного поля ферромагнетик перемагничивается (3 -4), и при достигается насыщение (4). Затем ферромагнетик можно опять размагнитить (4 -5 -6), и вновь намагнитить до насыщения (6 -1). При действии на магнетик переменного магнитного поля, намагниченность изменяется в соответствии с кривой 1 -2 -3 -4 -5 -6 -1 называемой ПЕТЛЕЙ ГИСТЕРЕЗИСА. Гистерезис приводит к тому, что намагничивание ферромагнетика не является однозначной функцией (одному и тому же значению соответствуют несколько значений ).

Зависимость от так же выражается с помощью петли гистерезиса, где остаточная индукция. Площадь петли гистерезиса пропорциональна количеству теплоты выделяющемуся в единице объема за один цикл перемагничивания. Ферромагнетики с малой коэрцитивной силой (узкой петлей гистерезиса) называются – мягкими (пределы от 0. 001 до 1 -2 А/см). Ферромагнетики с большой (от десятков до тысяч А/см) коэрцитивной силой называют жесткими. Жесткие ферромагнетики применяются для создания постоянных магнитов, мягкие используются для сердечников трансформаторов.

ТОЧКА КЮРИ. ДОМЕНЫ Для каждого ферромагнетика существует определенная температура – ТОЧКА КЮРИ, при которой он теряет свои свойства. При нагревании выше точки Кюри ферромагнетик превращается в парамагнетик. Переход сопровождается поглощением или выделением теплоты (фазовый переход второго рода). Ниже точки Кюри ферромагнетики обладают спонтанной намагниченностью, независимо от внешнего намагничивающего поля. Это происходит за счет разбиения ферромагнетика на большое количество малых макроскопических областей –ДОМЕНОВ, самопроизвольно намагниченных до насыщения. При отсутствии внешнего магнитного поля магнитные мо-

менты отдельных доменов ориентированы хаотически, и компенсируют друга, результирующий магнитный момент равен нулю и ферромагнетик не намагничен. Внешнее магнитное поле ориентирует по полю все магнитные моменты не отдельных атомов (как у парамагнетиков), а целых областей спонтанной намагниченности). При ослаблении внешнего магнитного поля до нуля, ферромагнетик сохраняет остаточное намагничивание, так как тепловое движение не в состоянии переориентировать магнитные моменты доменов. Поэтому наблюдается явление гистерезиса. Что бы размагнитить ферромагнетик, необходимо приложить коэрцитивную силу. Размагничиванию способствует так же ме-

ханическое воздействие на ферромагнетик, или его нагревание. Значит: Точка Кюри – температура , выше которой происходит разрушение доменной структуры. (линейные размеры доменов ≈10¯⁶-10¯⁴ м). Ферромагнетическими свойствами могут обладать только кристаллические тела.

УСЛОВИЯ ДЛЯ МАГНИТНОГО ПОЛЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД

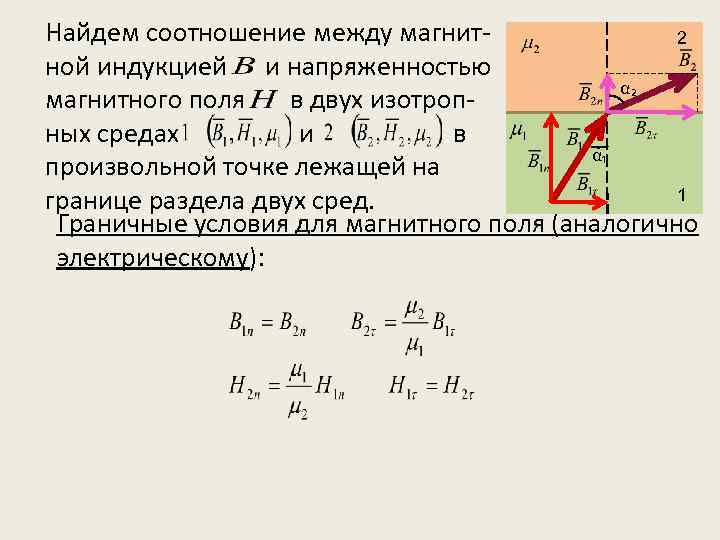Найдем соотношение между магнит2 ной индукцией и напряженностью α₂ магнитного поля в двух изотропных средах и в α₁ произвольной точке лежащей на 1 границе раздела двух сред. Граничные условия для магнитного поля (аналогично электрическому):

Граничные условия на границе раздела двух изотропных сред: • Если граница раздела двух сред ортогональна линиям магнитной индукции то и вектор магнитной индукции не изменяется при переходе через границу раздела сред: • Если граница раздела сред касается линий магнитной индукции и то и напряженность магнитного поля не изменяется при переходе через границу раздела сред.

• Если среда 1 вакуум то , значит: • Если углы между направлениями и к соответствующим нормалям, то закон преломления линий (а значит и линий ): Входя в магнетик с большей проницаемостью, линии и удаляются от нормали.

ОСНОВЫ ТЕОРИИ МАКСВЕЛЛА ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Из закона Фарадея следует, что любое изменение сцепленного с контуром потока электромагнитной индукции приводит к возникновению ЭДС самоиндукции, и из-за этого возникает индукционный ток. Однако, ЭДС в любой цепи возникает только тогда, когда в ней на носители тока действуют сторонние (не электрического происхождения) силы. Максвелл высказал гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной появления индукционного тока в контуре. Изменяющееся во времени магнитное поле порождает электрическое поле циркуляция которого равна:

Так как: Если поверхность и контур неподвижны, то справедливо выражение: Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна 0 Между рассматриваемыми полями и имеется принципиальное различие: циркуляция вектора , в отличие от не равна 0. значит электрическое поле возбуждаемое магнитным является ВИХРЕВЫМ.

ТОК СМЕЩЕНИЯ Согласно утверждению Максвелла: так как всякое переменное магнитное поле возбуждает в пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля, должно вызывать в окружающем пространстве появление вихревого магнитного поля. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем вводят понятие ТОК СМЕЩЕНИЯ. Пусть имеется цепь переменного тока включающая в себя конденсатор. Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, значит через

конденсатор «протекают» токи смещения, причем в тех участках где отсутствуют проводники. Переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками существовал ток проводимости, равный току в подводящих проводах. Поверхностная плотность заряда на обкладках конденсатора равна электрическому смещению в конденсаторе. Плотность тока смещения:

В диэлектриках: , и плотность тока смещения: – плотность тока смещения в вакууме – плотность тока поляризации (тока обусловленного упорядоченным движением электрических зарядов в диэлектрике). Принципиально новое в утверждении Максвелла то, что плотность тока смещения в вакууме, не связанная с движением зарядов, а обусловленная ТОЛЬКО изменением электрического поля во времени, ТОЖЕ ВОЗБУЖДАЕТ магнитное поле (даже в вакууме).

Максвелл ввел понятие ПОЛНОГО ТОКА равному сумме токов проводимости и смещения. Плотность полного тока: В цепях переменного тока полный ток всегда замкнут, то есть на концах проводника обрывается лишь ток проводимости, а в диэлектрике ( вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости. Максвелл обобщил теорему о циркуляции вектора

УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ Введение Максвеллом понятия тока смещения привело к созданию единой теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено. В основу теории Максвелла положены четыре уравнения :

1 уравнение Максвелла Электрическое поле может быть как потенциальным , так и вихревым , поэтому напряженность суммарного поля. Так как циркуляция вектора равна нулю, а для определяется как то циркуляция вектора напряженности суммарного электрического поля: Это показывает что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени электрические поля.

2 уравнение Максвелла Обобщенная теорема о циркуляции вектора напряженности магнитного поля показывает что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями:

3 уравнение Максвелла Теорема Гаусса для поля : Если заряд распределён внутри замкнутой поверхности непрерывно с объёмной плотностью , то формула имеет вид:

4 уравнение Максвелла Теорема Гаусса для поля : Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА В ИНТЕГРАЛЬНОЙ ФОРМЕ Связь между величинами входящими в уравнения Максвелла:

Для стационарных полей ( ния Максвелла имеют вид: ) уравне- Уравнения Максвелла показали, что переменное магнитное поле всегда связано с порождаемым ей электрическим полем и наоборот. То есть электрическое и магнитное поля неразрывно связаны друг с другом. Они образуют единое: ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ