ЛЕКЦИЯ 5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. УРАВНЕНИЯ МАКСВЕЛЛА 5. 1

ЛЕКЦИЯ 5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. УРАВНЕНИЯ МАКСВЕЛЛА 5. 1 Закон электромагнитной индукции. Правило Ленца

Открытие Фарадея В 1831 г. Фарадеем было сделано одно из наиболее фундаментальных открытий в электродинамике – явление электромагнитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении магнитного потока (т. е. потока вектора B), охватываемого этим контуром, возникает электрический ток – его называют индукционным.

Открытие Фарадея Появление индукционного тока означает, что при изменении магнитного потока в контуре возникает ЭДС индукции i. При этом i не зависит от способа изменения магнитного потока, а определяется лишь скоростью его изменения, т. е. d /dt. Изменение знака производной d /dt приводит к изменению знака i т. е. и направления тока в контуре.

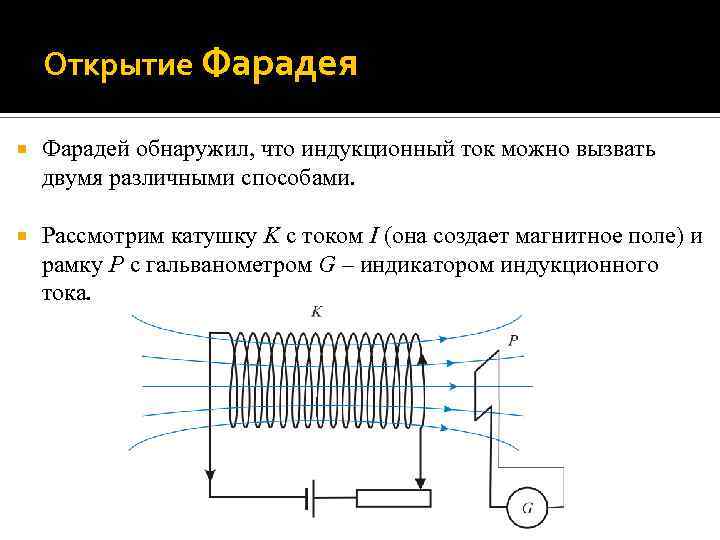Открытие Фарадея Фарадей обнаружил, что индукционный ток можно вызвать двумя различными способами. Рассмотрим катушку K с током I (она создает магнитное поле) и рамку P с гальванометром G – индикатором индукционного тока.

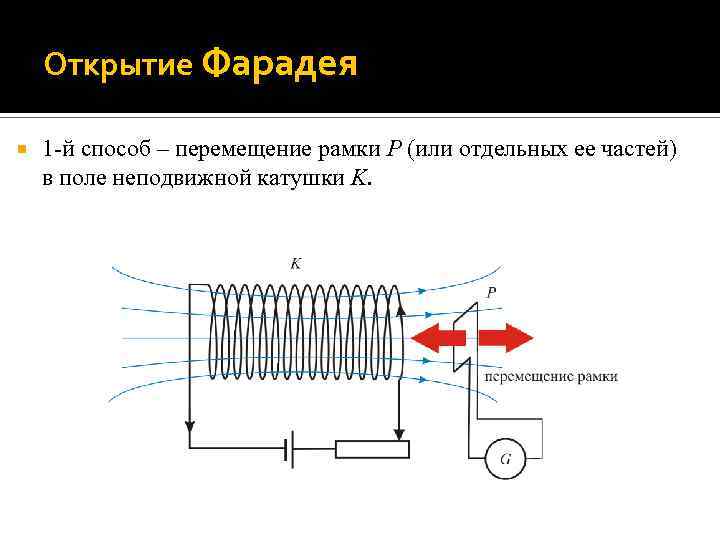Открытие Фарадея 1 -й способ – перемещение рамки P (или отдельных ее частей) в поле неподвижной катушки K.

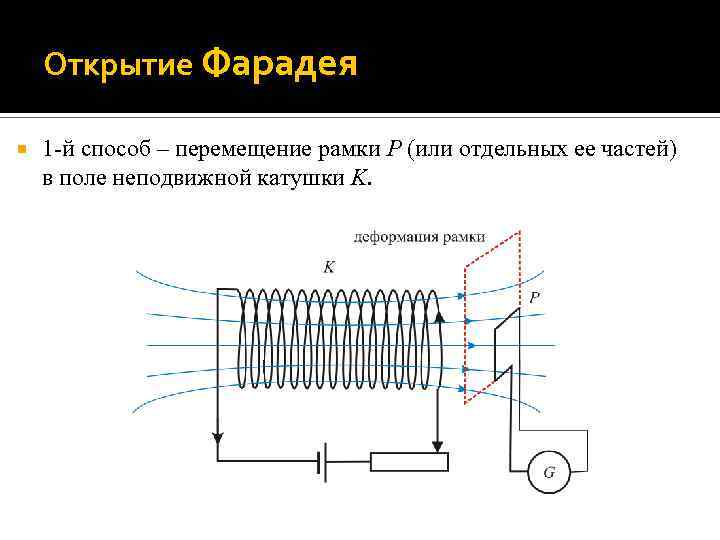Открытие Фарадея 1 -й способ – перемещение рамки P (или отдельных ее частей) в поле неподвижной катушки K.

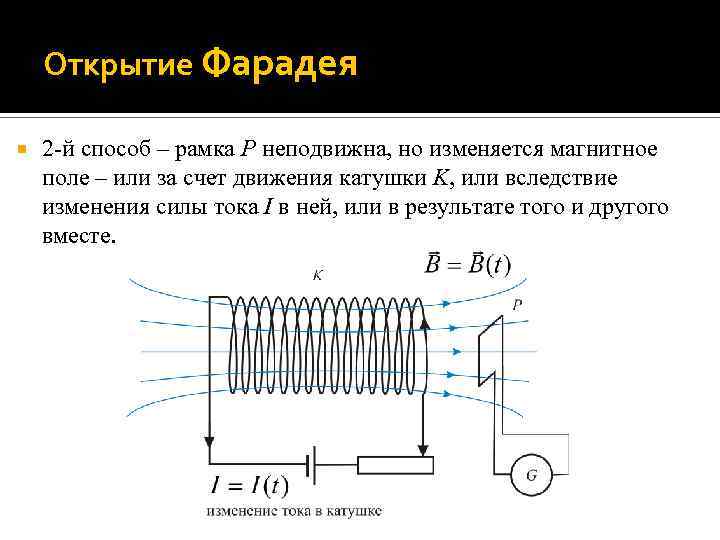
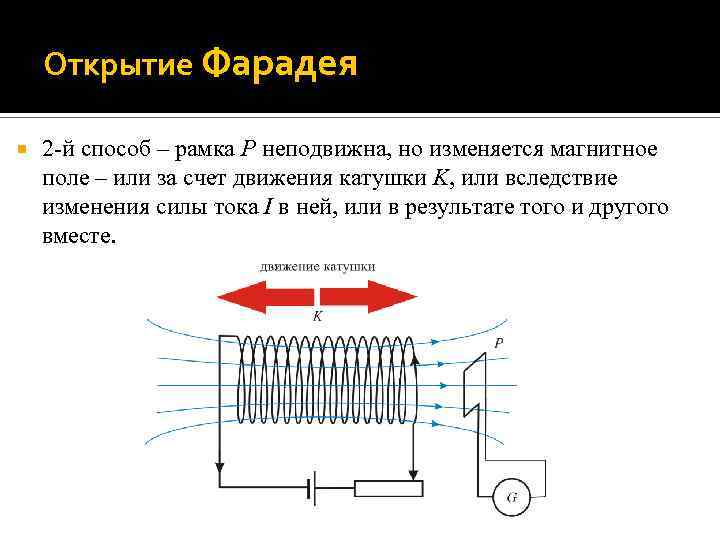Открытие Фарадея 2 -й способ – рамка P неподвижна, но изменяется магнитное поле – или за счет движения катушки K, или вследствие изменения силы тока I в ней, или в результате того и другого вместе.

Открытие Фарадея 2 -й способ – рамка P неподвижна, но изменяется магнитное поле – или за счет движения катушки K, или вследствие изменения силы тока I в ней, или в результате того и другого вместе.

Правило Ленца Направление индукционного тока (а значит и знак ЭДС индукции) определяется правилом Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает такое магнитное поле, магнитный поток которого препятствует изменению магнитного потока, вызывающего ЭДС индукции.

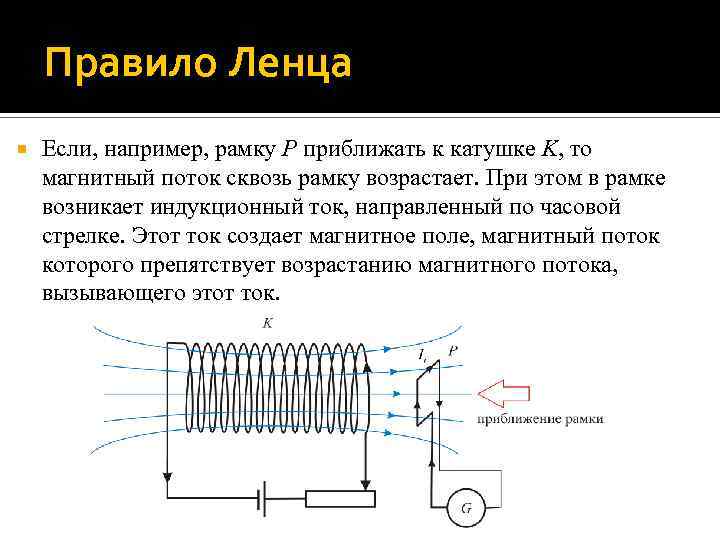Правило Ленца Если, например, рамку P приближать к катушке K, то магнитный поток сквозь рамку возрастает. При этом в рамке возникает индукционный ток, направленный по часовой стрелке. Этот ток создает магнитное поле, магнитный поток которого препятствует возрастанию магнитного потока, вызывающего этот ток.

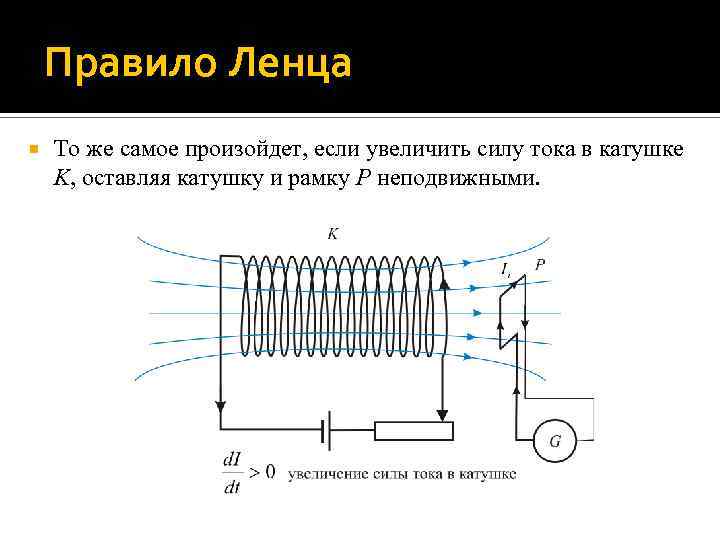Правило Ленца То же самое произойдет, если увеличить силу тока в катушке K, оставляя катушку и рамку P неподвижными.

Правило Ленца выражает существенный физический факт – стремление системы противодействовать изменению ее состояния (электромагнитная инерция)

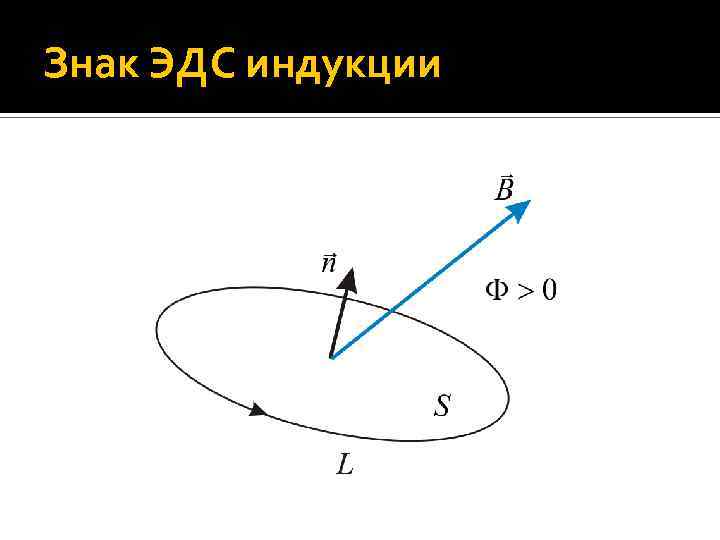
Закон электромагнитной индукции Согласно этому закону, какова бы ни была причина изменения магнитного потока, охватываемого проводящим контуром, возникающая в контуре ЭДС индукции определяется формулой Знак «минус» в этом уравнении связан с определенным правилом знаков и отражает правило Ленца. Знак магнитного потока связан с выбором нормали к поверхности S, ограниченной рассматриваемым контуром, а знак ЭДС индукции и тока – с выбором положительного направления обхода по контуру.

Знак ЭДС индукции

Закон электромагнитной индукции Здесь предполагается, что направление нормали n к поверхности S контура и положительное направление обхода контура связаны друг с другом правилом правого винта. Поэтому, выбирая (произвольно) направление n, мы определяем и знак потока , и знак ЭДС индукции в контуре. Единицей магнитного потока является вебер (Вб). При скорости изменения магнитного потока 1 Вб/с в контуре индуцируется ЭДС индукции, равная 1 В.

Полный магнитный поток Если замкнутый контур, в котором индуцируется ЭДС, состоит из N витков (например, соленоид), то ЭДС i будет равна сумме ЭДС, индуцируемых в каждом из витков. Если при этом магнитный поток, охватываемый каждым витком, одинаков и равен 1, то суммарный поток сквозь поверхность этого сложного контура можно представить как Эта величина называется потокосцеплением, или полным магнитным потоком. В этом случае ЭДС индукции

ЛЕКЦИЯ 5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ УРАВНЕНИЯ МАКСВЕЛЛА 5. 2 Природа электромагнитной индукции

Природа электромагнитной индукции Существуют две принципиально разные причины, которые могут вызвать изменение магнитного потока через поверхность замкнутого контура: (1) при неизменном магнитном поле изменение положения контура в пространстве (его перемещение, вращение, деформация); (2) при неизменной форме контура и неизменном его положении в пространстве изменение с течением времени индукции B магнитного поля.

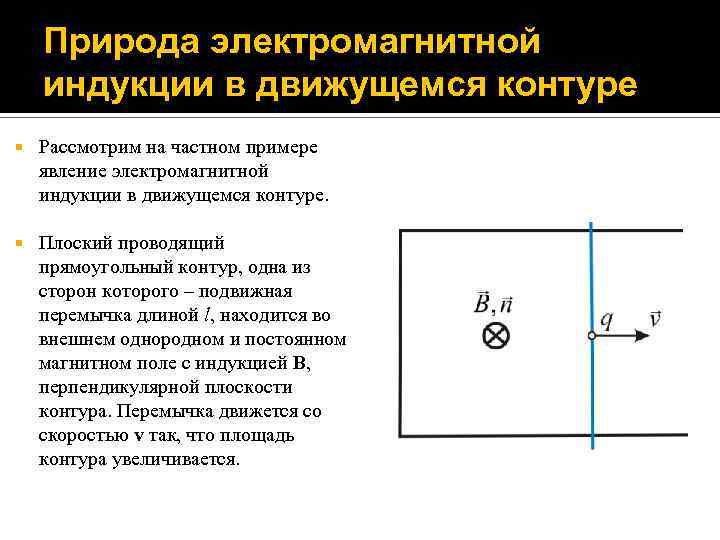Природа электромагнитной индукции в движущемся контуре Рассмотрим на частном примере явление электромагнитной индукции в движущемся контуре. Плоский проводящий прямоугольный контур, одна из сторон которого – подвижная перемычка длиной l, находится во внешнем однородном и постоянном магнитном поле с индукцией B, перпендикулярной плоскости контура. Перемычка движется со скоростью v так, что площадь контура увеличивается.

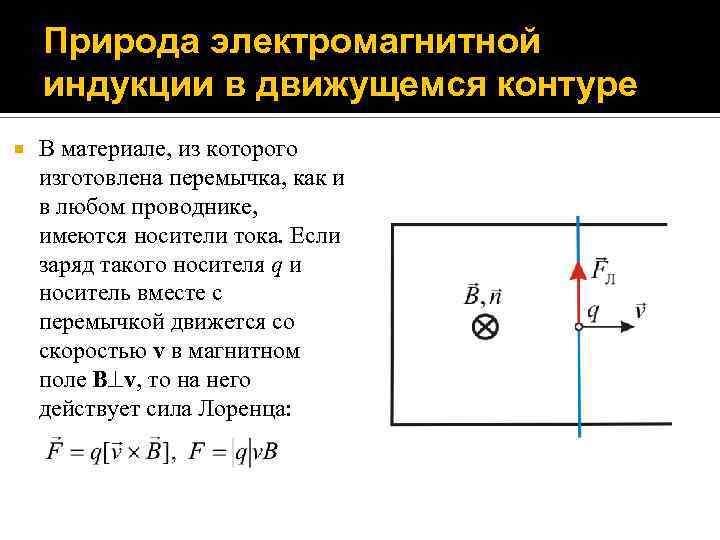Природа электромагнитной индукции в движущемся контуре В материале, из которого изготовлена перемычка, как и в любом проводнике, имеются носители тока. Если заряд такого носителя q и носитель вместе с перемычкой движется со скоростью v в магнитном поле B v, то на него действует сила Лоренца:

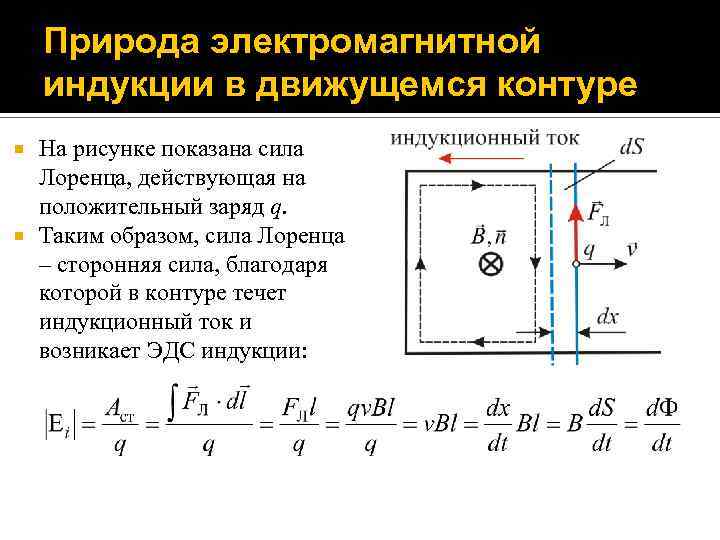Природа электромагнитной индукции в движущемся контуре На рисунке показана сила Лоренца, действующая на положительный заряд q. Таким образом, сила Лоренца – сторонняя сила, благодаря которой в контуре течет индукционный ток и возникает ЭДС индукции:

Природа электромагнитной индукции в движущемся контуре Определим знак ЭДС индукции. Если выбрать единичный вектор нормали n B, то > 0 и d > 0. При этом сторонняя сила – сила Лоренца – противоположна положительному направлению обхода контура, связанному правилом правого винта с направлением n. Следовательно, Таким образом, во всех случаях, когда в неизменном магнитном поле изменяется положение контура в пространстве, появление ЭДС индукции в контуре связано с действие сила Лоренца на движущиеся заряды.

Природа электромагнитной индукции в покоящемся контуре Если замкнутый проводящий контур, расположенный в магнитном поле, неподвижен, а само поле изменяется с течением времени, что в контуре возникает ЭДС индукции и течет индукционный ток. Для объяснения этого явления Максвелл предположил, и это было подтверждено многочисленными опытами, что изменяющееся во времени магнитное поле с индукцией B порождает в пространстве (независимо от наличия или отсутствия проводящего контура) электрическое поле с напряженностью E, которое является вихревым электрическим полем. Силовые линии вихревого электрического поля замкнуты.

Природа электромагнитной индукции в покоящемся контуре

Природа электромагнитной индукции в покоящемся контуре Если силовая линия поля замкнута, работа поля при перемещении заряда по замкнутому и совпадающему с силовой линией замкнутому контуру отлична от нуля. Таким образом, справедливая для стационарного электрического поля теорема о циркуляции вектора E (циркуляция вектора напряженности E электростатического поля вдоль произвольного замкнутого контура равна нулю) не выполняется для вихревого электрического поля. В этом состоит принципиальное отличие вихревого электрического поля от электростатического.

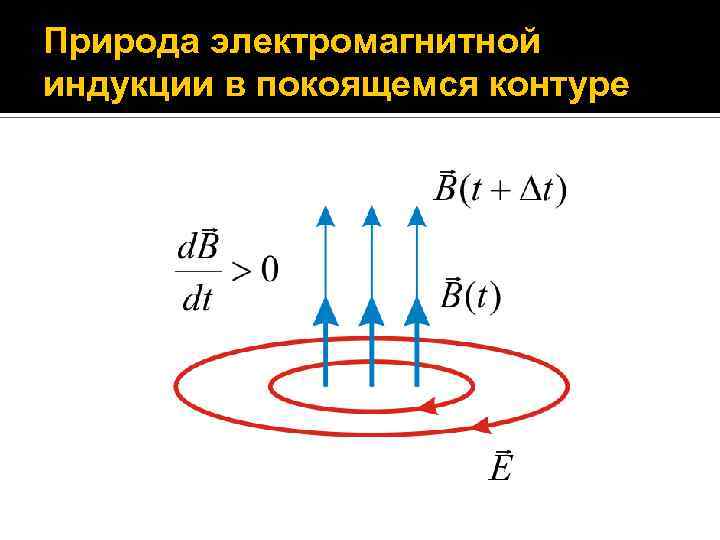
Природа электромагнитной индукции в покоящемся контуре Если в области пространства, где существует вихревое электрическое поле, расположен проводящий замкнутый контур, то имеющиеся в проводнике носители тока под действием сил вихревого электрического поля будут перемещаться по контуру и потечет индукционный ток. При этом сам контур не является необходимым условием возникновения такого поля. Он – лишь его индикатор.

Уравнение Максвелла Пусть в покоящемся замкнутом проводящем контуре L в результате изменения поля B наблюдается явление электромагнитной индукции. ЭДС индукции: Силы вихревого электрического поля E рассматриваются как сторонние силы, работа которых по переносу единичного положительного заряда:

Уравнение Максвелла Рассмотрим правую часть закон Фарадея: Здесь учтено, что B = B(x, y, z, t). Таким образом, Это уравнение называется уравнением Максвелла. Оно является обобщением теоремы о циркуляции вектора напряженности E электрического поля для случая произвольных полей.

Уравнение Максвелла Действительно, если в пространстве, помимо вихревого электрического поля имеется и электростатическое, то Тогда циркуляция вектора E Таким образом, наличие в пространстве электростатического поля, созданного неподвижными зарядами, не нарушает уравнения Максвелла.

ЛЕКЦИЯ 5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. УРАВНЕНИЯ МАКСВЕЛЛА 5. 3 Явление самоиндукции

Индуктивность Пусть замкнутый проводящий контур находится в свободном от внешних магнитных полей пространстве. Если по контуру пропустить электрический ток, то вокруг него возникнет собственное магнитное поле, порождаемое им. Можно показать (используя закон Био – Савара – Лапласа), что магнитный поток через поверхность контура пропорционален силе тока в нем:

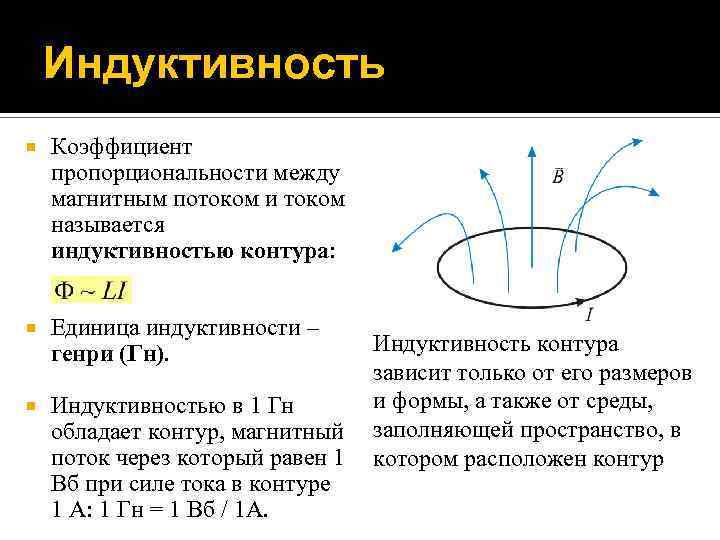Индуктивность Коэффициент пропорциональности между магнитным потоком и током называется индуктивностью контура: Единица индуктивности – генри (Гн). Индуктивностью в 1 Гн обладает контур, магнитный поток через который равен 1 Вб при силе тока в контуре 1 А: 1 Гн = 1 Вб / 1 А. Индуктивность контура зависит только от его размеров и формы, а также от среды, заполняющей пространство, в котором расположен контур

Индуктивность Как известно, магнитный поток через ограниченную контуром поверхность S равен Магнитная индукция B в любой точке поверхности интегрирования S, согласно закону Био – Савара – Лапласа: Из формул следует, что при увеличении силы тока I в n раз, в любой точке контура магнитное поле B тоже увеличивается в n раз; соответственно в n раз увеличивается магнитный поток через поверхность контура. Таким образом, ~ I.

Индуктивность соленоида В качестве примера вычислим индуктивность соленоида длины l и площадью поперечного сечения S, число витков на единицу длины которого равно n. Будем считать, что длина соленоида велика по сравнению с его диаметром, поэтому справедлива формула для магнитной индукции B бесконечно длинного соленоида: Здесь I – сила тока, текущего в проводе, из которого изготовлена обмотка соленоида.

Индуктивность соленоида Если полное число витков соленоида равно N = nl, то магнитный поток через соленоид равен произведению магнитного потока 1 через один виток соленоида и числа его витков: Тогда индуктивность соленоида Здесь V = Sl – объем соленоида.

Явление самоиндукции Рассмотрим замкнутый проводящий контур с индуктивностью L, по которому течет силой I. Магнитный поток через поверхность контура равен: = LI. При изменении силы тока I магнитный поток также будет меняться, и в соответствии с законом электромагнитной индукции Фарадея, в контуре возникнет ЭДС индукции, потечет индукционный ток Ii. В этом случае явление электромагнитной индукции называется самоиндукцией.

Явление самоиндукции Самоиндукция – это явление возникновения ЭДС индукции и индукционного тока в замкнутом проводящем контуре за счет изменения силы тока в этом контуре. ЭДС самоиндукции si как частный случай ЭДС индукции рассчитывается по формуле: При этом предполагается, что в процессе изменения силы тока в контуре геометрические размеры контура не изменяются, а также в контуре отсутствует ферромагнитный сердечник (т. е. L = const).

Явление самоиндукции Знак «минус» в формуле показывает, что индукционный ток (и ЭДС самоиндукции) в контуре имеют такое направление, чтобы противодействовать изменению тока силы I, которое служит причиной возникновения самоиндукции. Например, если сила тока увеличивается (d. I/dt > 0), то si < 0, т. е. индукционный ток Ii будет течь в направлении, противоположном увеличивающему току I.

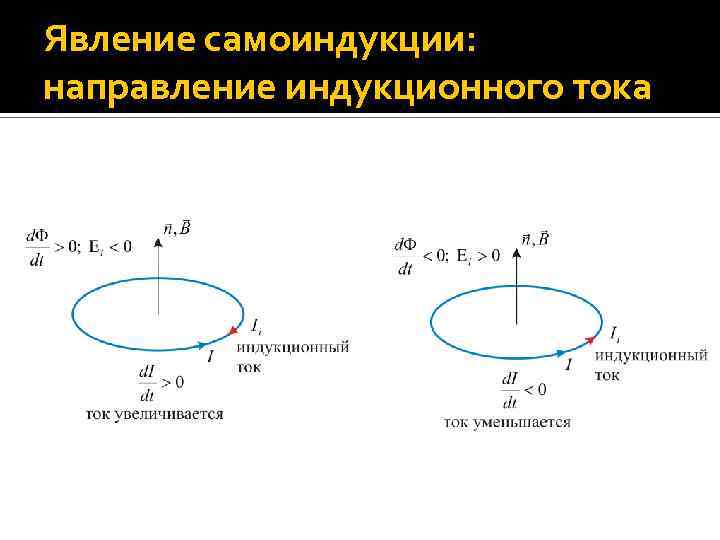Явление самоиндукции: направление индукционного тока

Установление тока в цепи, содержащей большую индуктивность Если электрическая цепь, по которой течет ток, обладает большой индуктивностью, то при размыкании цепи резкое уменьшение силы тока до нуля приводит к возникновению ЭДС самоиндукции большой величины. В том месте, где происходит разрыв цепи (между контактами выключателя), проскакивает искра (искровой разряд). Рассмотрим причину этого явления. Размыкание цепи, по которой течет ток, можно рассматривать как включение в цепь большого сопротивления (сопротивление воздушного промежутка между контактами выключателя).

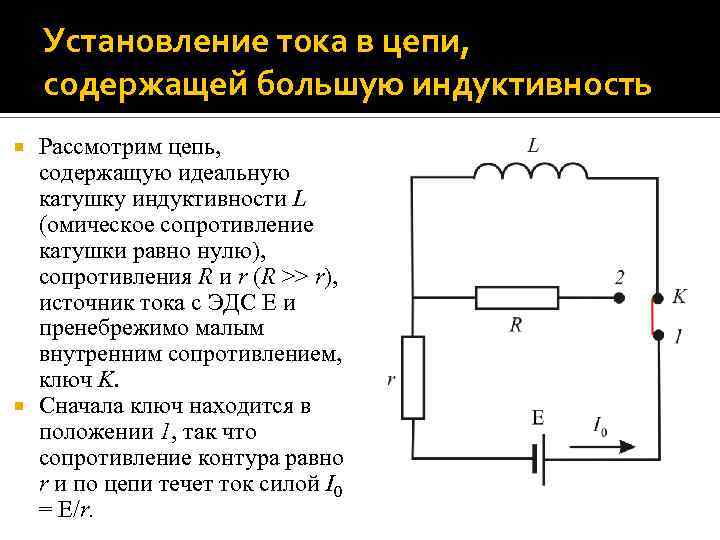Установление тока в цепи, содержащей большую индуктивность Рассмотрим цепь, содержащую идеальную катушку индуктивности L (омическое сопротивление катушки равно нулю), сопротивления R и r (R >> r), источник тока с ЭДС и пренебрежимо малым внутренним сопротивлением, ключ K. Сначала ключ находится в положении 1, так что сопротивление контура равно r и по цепи течет ток силой I 0 = /r.

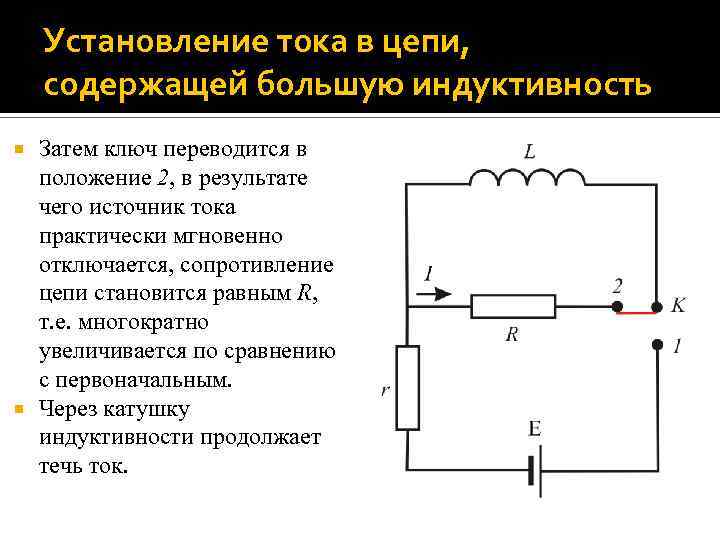Установление тока в цепи, содержащей большую индуктивность Затем ключ переводится в положение 2, в результате чего источник тока практически мгновенно отключается, сопротивление цепи становится равным R, т. е. многократно увеличивается по сравнению с первоначальным. Через катушку индуктивности продолжает течь ток.

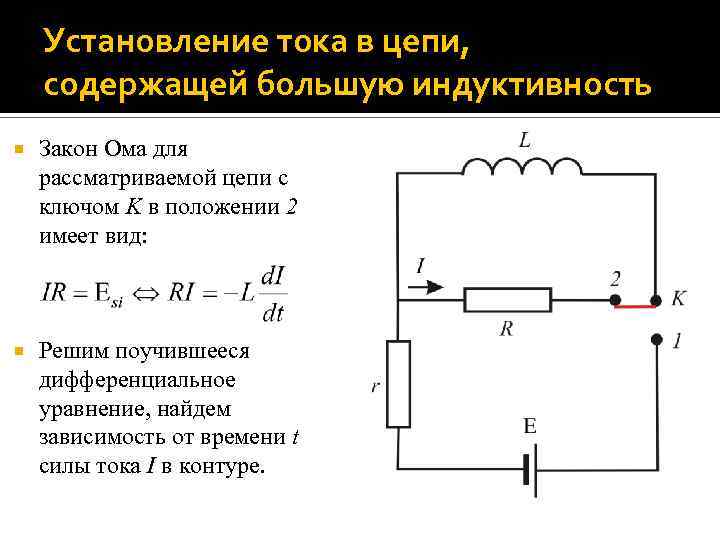Установление тока в цепи, содержащей большую индуктивность Закон Ома для рассматриваемой цепи с ключом K в положении 2 имеет вид: Решим поучившееся дифференциальное уравнение, найдем зависимость от времени t силы тока I в контуре.

Установление тока в цепи, содержащей большую индуктивность Имеем: Тогда

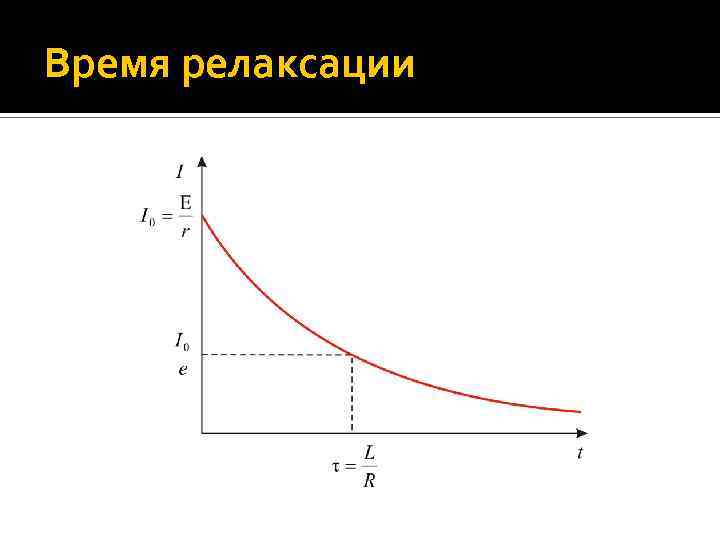
Установление тока в цепи, содержащей большую индуктивность Как следует из получившегося выражения, время релаксации, т. е. время, в течение которого сила тока в цепи уменьшится в e раз, составляет величину: Таким образом, чем больше индуктивность контура (цепи), тем медленней будем уменьшаться ток в ней при его выключении.

Время релаксации

Установление тока в цепи, содержащей большую индуктивность Вычислим напряжение U на концах катушки индуктивности, равное возникающей в ней ЭДС индукции: Поскольку сопротивление R служит моделью воздушного промежутка между контактами выключателя реальных цепей, данное выражение дает возможность проанализировать физические факторы, способствующие электрическому пробою воздушного промежутка.

Установление тока в цепи, содержащей большую индуктивность Согласно этой формуле, U ~ R/r, а, поскольку отношение R/r представляет собой огромную величину, то напряжение U между контактами выключателя сразу же после разрыва цепи, равно: U = R/r также очень велико: оно многократно превышает ЭДС источника тока. Вместе с этим, величина U не зависит от индуктивности L катушки. Тогда почему же искрение между контактами выключателя тем больше, чем больше индуктивность?

Установление тока в цепи, содержащей большую индуктивность Чтобы произошел пробой воздушного промежутка (т. е. искрение), высокое напряжение между контактами выключателя должно поддерживаться в течение определенного (достаточного для лавинообразного нарастания тока в газовой среде) времени. Характерное время , в течение которого после переключения ключа из положения 1 в положение 2 в цепи течет ток и поддерживается большое напряжение на сопротивлении R, тем больше, чем больше индуктивность L катушки. С увеличением L время , и, соответственно, вероятность возникновения искрового разряда в воздушном промежутке между контактами выключателя возрастает.

ЛЕКЦИЯ 5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. УРАВНЕНИЯ МАКСВЕЛЛА 5. 4 Энергия магнитного поля

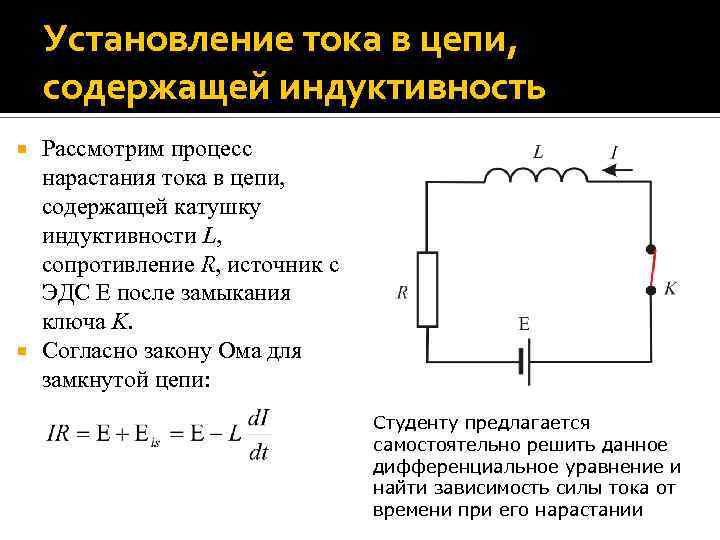Установление тока в цепи, содержащей индуктивность Рассмотрим процесс нарастания тока в цепи, содержащей катушку индуктивности L, сопротивление R, источник с ЭДС после замыкания ключа K. Согласно закону Ома для замкнутой цепи: Студенту предлагается самостоятельно решить данное дифференциальное уравнение и найти зависимость силы тока от времени при его нарастании

Магнитная энергия контура с током Умножим это уравнение на величину I и приведем его к виду: Это равенство представляет собой закон сохранения энергии: I – мощность сторонних сил, которая затрачивается источником тока на выделение теплоты на сопротивлении R и увеличение энергии катушки: I 2 R – тепловая мощность тока, LI 2/2 – магнитная энергия катушки, а d(LI 2/2)/dt – приращение энергии катушки в единицу времени.

Магнитная энергия контура с током Таким образом, величина представляет собой энергию катушки с током или магнитную энергию контура Учитывая, что магнитный поток через катушку индуктивности L равен LI, то энергию контура можно представить в форме:

Энергия магнитного поля Магнитную энергию катушки LI 2/2 можно интерпретировать как энергию имеющегося в катушке магнитного поля и выразить ее через параметры самого поля – магнитную индукцию B и напряженность H (B = 0 H). Покажем это на примере бесконечно длинного соленоида. Воспользуемся формулой его индуктивности: Здесь – магнитная проницаемость вещества, заполняющего соленоид, n – число витков на единицу длины соленоида, V – объем соленоида

Энергия магнитного поля Магнитная индукция B внутри соленоида: Тогда магнитную энергию можно представить в виде Магнитное поле соленоида является однородным. Разделив магнитную энергию поля в соленоиде на его объем V, найдем объемную плотность энергии магнитного поля:

Энергия магнитного поля Можно показать, что в общем случае магнитного поля (в том числе и неоднородного) с индукцией B и напряженностью H объемная плотность энергии рассчитывается по формуле: Объемная плотность энергии w является характеристикой поля в данной точке пространства. Если параметры B и H от точки к точке меняются, то эта формула все равно остается справедливой. Тогда энергия магнитного поля в конечном объеме пространства:

ЛЕКЦИЯ 5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. УРАВНЕНИЯ МАКСВЕЛЛА 5. 5 Взаимная индукция

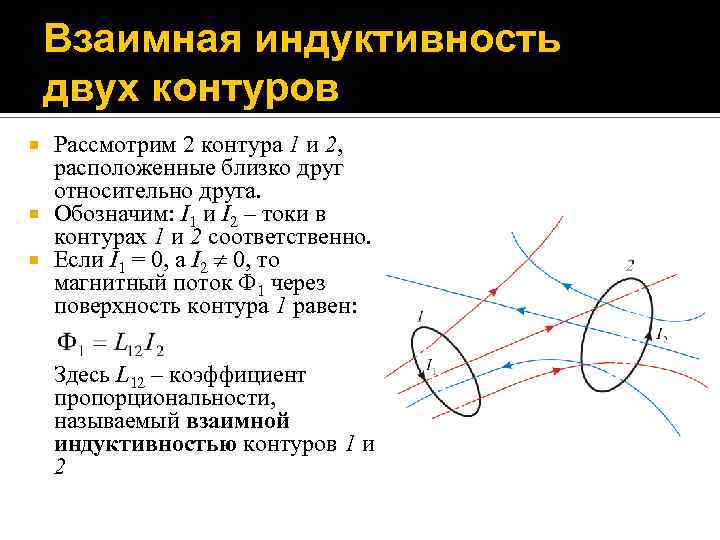Взаимная индуктивность двух контуров Рассмотрим 2 контура 1 и 2, расположенные близко друг относительно друга. Обозначим: I 1 и I 2 – токи в контурах 1 и 2 соответственно. Если I 1 = 0, а I 2 0, то магнитный поток 1 через поверхность контура 1 равен: Здесь L 12 – коэффициент пропорциональности, называемый взаимной индуктивностью контуров 1 и 2

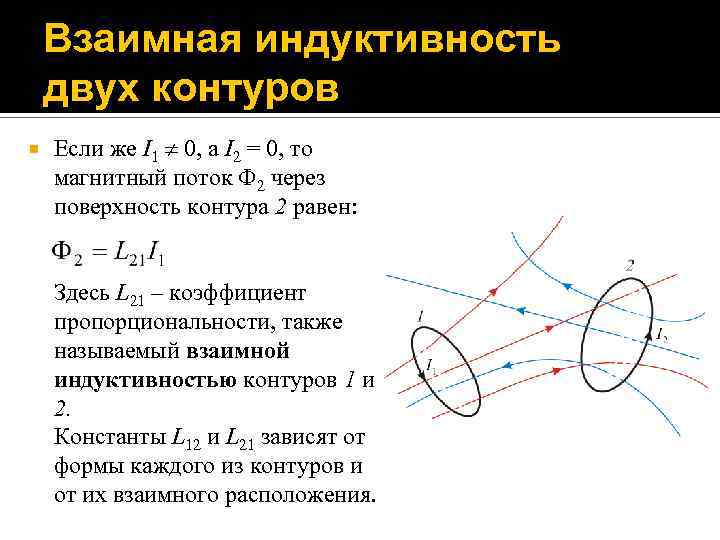Взаимная индуктивность двух контуров Если же I 1 0, а I 2 = 0, то магнитный поток 2 через поверхность контура 2 равен: Здесь L 21 – коэффициент пропорциональности, также называемый взаимной индуктивностью контуров 1 и 2. Константы L 12 и L 21 зависят от формы каждого из контуров и от их взаимного расположения.

Теорема взаимности Согласно теореме взаимности, для любых двух контуров, между которыми имеется магнитная связь, взаимные индуктивности L 12 и L 21 одинаковы: Доказательство этой теоремы мы не приводим. Отметим, что в соответствии с определением индуктивности L контура, благодаря такому выбору направления нормали n к поверхности контура, при котором магнитный поток и ток I имеют одинаковые знаки, индуктивность L > 0. Напротив, взаимная индуктивность двух контуров может быть как положительной, так и отрицательной.

Взаимная индукция Взаимной индукцией называется явление возникновения ЭДС индукции в одном из контуров, между которыми имеется магнитная связь, за счет изменения силы тока в другом контуре.

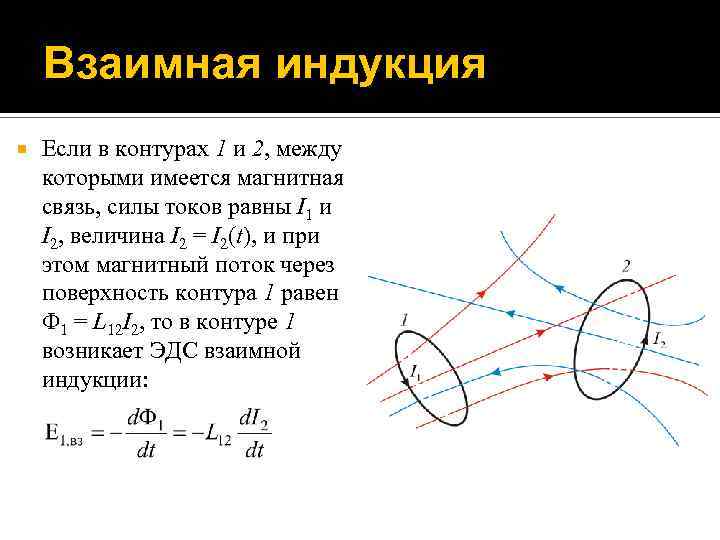Взаимная индукция Если в контурах 1 и 2, между которыми имеется магнитная связь, силы токов равны I 1 и I 2, величина I 2 = I 2(t), и при этом магнитный поток через поверхность контура 1 равен 1 = L 12 I 2, то в контуре 1 возникает ЭДС взаимной индукции:

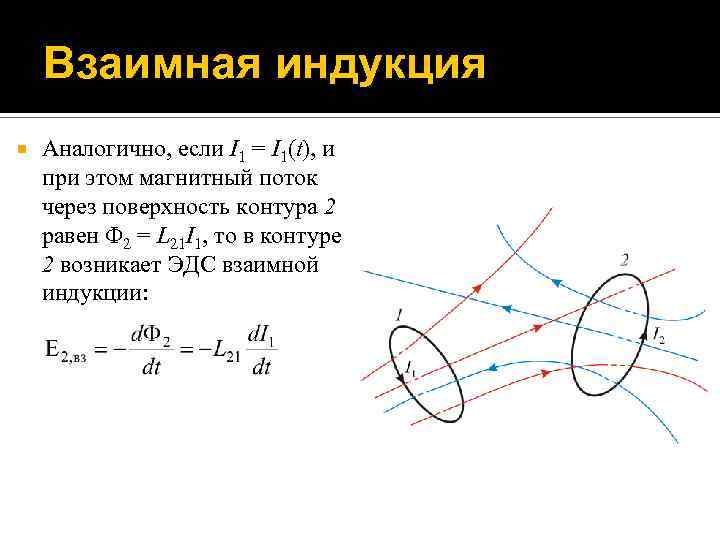Взаимная индукция Аналогично, если I 1 = I 1(t), и при этом магнитный поток через поверхность контура 2 равен 2 = L 21 I 1, то в контуре 2 возникает ЭДС взаимной индукции:

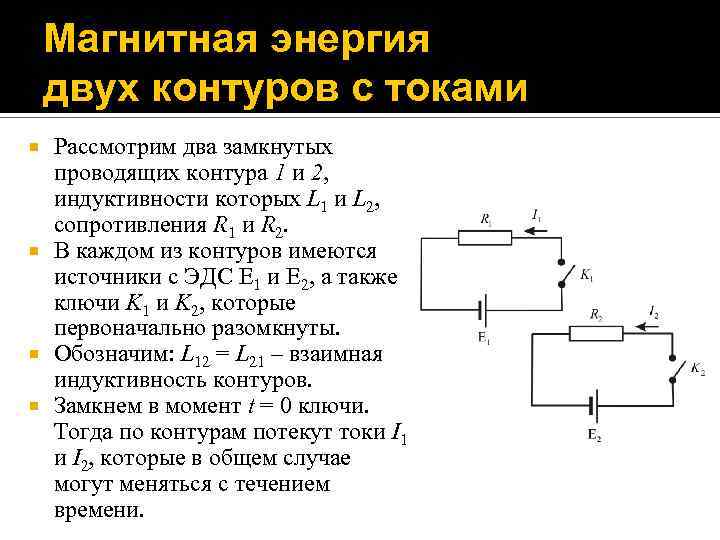Магнитная энергия двух контуров с токами Рассмотрим два замкнутых проводящих контура 1 и 2, индуктивности которых L 1 и L 2, сопротивления R 1 и R 2. В каждом из контуров имеются источники с ЭДС 1 и 2, а также ключи K 1 и K 2, которые первоначально разомкнуты. Обозначим: L 12 = L 21 – взаимная индуктивность контуров. Замкнем в момент t = 0 ключи. Тогда по контурам потекут токи I 1 и I 2, которые в общем случае могут меняться с течением времени.

Магнитная энергия двух контуров с токами Запишем закон Ома для контура 1: За время dt сторонние силы источника тока, имеющегося в контуре 1, совершат работу A 1 = I 1 1 dt, величину которой выразим с помощью предыдущего уравнения:

Магнитная энергия двух контуров с токами Аналогично можно показать, что сторонние силы источника тока в контуре 2 за то же время совершат работу Суммарная работа сторонних сил источников в контурах 1 и 2: Здесь Q 1 и Q 2 – количества теплоты, выделяющейся на сопротивлениях R 1 и R 2 (в соответствии с законом Джоуля Ленца).

Магнитная энергия двух контуров с токами Интегрируя обе части последнего равенства, найдем работу сторонних сил к некоторому моменту времени, когда силы токов в контурах достигнут значений I 1 и I 2 соответственно: Таким образом, работа A сторонних сил источников тока затрачивается на выделение теплоты Q 1 и Q 2 и на накопление магнитной энергии L 1 I 12/2 и L 2 I 22/2 контурами 1 и 2, соответственно. Слагаемое L 12 I 1 I 2 представляет собой выражение для взаимной магнитной энергии контуров, между которыми имеется магнитная связь и в которых текут токи I 1 и I 2.

ЛЕКЦИЯ 5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. УРАВНЕНИЯ МАКСВЕЛЛА 5. 6 Ток смещения. Теорема о циркуляции вектора H для переменных токов

Теорема о циркуляции вектора напряженности магнитного поля переменных токов. Ток смещения Сначала введем определения, которые потребуются для описания свойств электромагнитного поля. Напомним, что сила тока I, текущего через некоторую поверхность S, определяется как интеграл от плотности тока j по поверхности S: Плотностью тока смещения jсм называется производная по времени вектора электрической индукции (вектора электрического смещения):

Теорема о циркуляции вектора напряженности магнитного поля переменных токов. Ток смещения Отметим, что вектор D зависит не только от времени t, но и от пространственных координат x, y, z, а именно: D = D(x, y, z, t). Обозначим через jпр плотность тока проводимости, т. е. тока, обусловленного упорядоченным движением свободных зарядов в проводящей среде. Плотностью полного тока будем называть сумму плотностей тока проводимости и смещения:

Теорема о циркуляции вектора напряженности магнитного поля переменных токов. Ток смещения Сила полного тока I, текущего через произвольную поверхность S, и плотность j полного тока в точках этой поверхности связаны соотношением:

Теорема о циркуляции вектора H Рассмотрим участок электрической цепи, в состав которой входит плоский конденсатор. Пусть конденсатор заряжается, тогда величина заряда положительной обкладки q и сила тока в подводящих проводах зависят от времени. Будем полагать, что размеры платин велики по сравнением с расстоянием между ними, т. е. электрической поле конденсатора сосредоточено между пластинами и однородно, а снаружи оно равно нулю.

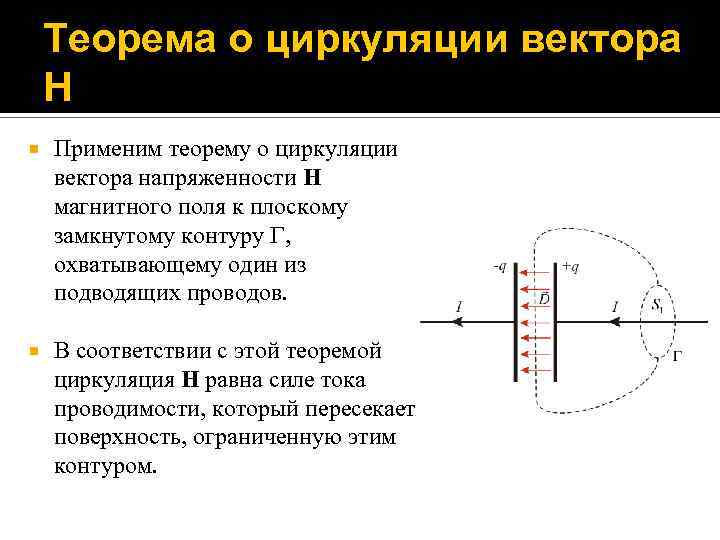Теорема о циркуляции вектора H Применим теорему о циркуляции вектора напряженности H магнитного поля к плоскому замкнутому контуру , охватывающему один из подводящих проводов. В соответствии с этой теоремой циркуляция H равна силе тока проводимости, который пересекает поверхность, ограниченную этим контуром.

Теорема о циркуляции вектора H Рассмотрим две ограниченные контуром поверхности S 1 и S 2, одна из которых (S 1) плоская и пересекает проводник, а вторая (S 2) такова, что ее часть располагается между обкладками конденсатора, не касаясь их. Тогда теорема о циркуляции становится неоднозначной:

Теорема о циркуляции вектора H Кроме того, если справедливо второе равенство, из которого следует, что H = 0, т. е. магнитное поле в пространстве около проводника с током силой I вообще отсутствует. Это утверждение не согласуется с опытом.

Теорема о циркуляции вектора H Причина противоречий состоит в следующем. Теорема о циркуляции вектора H в форме справедлива для магнитного поля постоянных токов и не применима для описания свойств магнитного поля переменных токов (в рассматриваемом примере сила тока I в подводящих проводах в процессе зарядки конденсатора изменяется с течением времени). Поэтому применять теорему о циркуляции в такой форме нельзя. Ее необходимо подвергнуть корректировке.

Теорема о циркуляции вектора H Теорема о циркуляции вектора H, справедливая для описания свойства магнитного поля как постоянных, так и переменных токов: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру равна силе полного тока, охватываемого этим контуром или, иначе говоря, пересекающего ограниченную контуром поверхность S:

Теорема о циркуляции вектора H Вернемся к расчету тока, пересекающего поверхность S 1. Поскольку электрическое поле конденсатора сосредоточено только между его пластинами, а вне конденсатора равно нулю, то поверхность S 1 не пересекается токами смещения:

Теорема о циркуляции вектора H Рассмотрим теперь токи, пересекающие поверхность S 2. Ток проводимость поверхность S 2 не пересекает. Его пересекает только ток смещения в конденсаторе: Таким образом, применение теоремы о циркуляции в откорректированном виде приводит к одному и тому же результату.

Физический смысл теоремы о циркуляции вектора H Из него следует, что в пространстве, где нет токов проводимости (jпр = 0), но существует изменяющееся со временем электрическое поле (jсм = д. D/дt) циркуляция вектора H не равна нулю. Следовательно, магнитное поле может существовать и в отсутствии токов проводимости; оно порождается изменяющемся со временем электрическим полем. Дифференциальная форма теорема о циркуляции вектора H:

ЛЕКЦИЯ 5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. УРАВНЕНИЯ МАКСВЕЛЛА 5. 7 Уравнения Максвелла

Уравнения Максвелла Английским ученым Максвеллом (1831 – 1879 г. ) была создана теория электрических и магнитных полей. Она с единой точки зрения объяснила разрозненные явления электричества и магнетизма, предсказала ряд новых явлений, существование которых было подтверждено впоследствии. Всю картину электромагнитных явлений можно представить в виде системы фундаментальных уравнений электродинамики, называемых уравнениями Максвелла. Эти уравнения нельзя вывести, они являются аксиомами, постулатами электродинамики, полученными путем обобщения опытных данных.

1 -е уравнение Максвелла Поток вектора электрической индукции D через произвольную замкнутую поверхность S равен стороннему заряду q, расположенному внутри этой поверхности: Дифференциальная форма 1 -го уравнения Максвелла:

2 -е уравнение Максвелла Поток вектора магнитной индукции B через произвольную замкнутую поверхность S равен нулю: Дифференциальная форма 2 -го уравнения Максвелла: Это уравнение отражает тот факт, что в природе не обнаружены магнитные заряды, и силовые линии магнитного поля являются замкнутыми.

3 -е уравнение Максвелла Циркуляция вектора напряженности электрического поля E по произвольному замкнутому контуру равна: Дифференциальная форма 3 -го уравнения Максвелла: Это уравнение является следствием закон электромагнитной индукции Фарадея и отражает тот факт, что переменное магнитное поле порождает в пространстве вихревое электрическое поле, силовые линии которого замкнуты.

4 -е уравнение Максвелла Циркуляция вектора напряженности магнитного поля H по произвольному замкнутому контуру равна полному току, пересекающему поверхность, ограниченную контуром: Дифференциальная форма 4 -го уравнения Максвелла: Это уравнение отражает тот факт, что переменное электрическое поле порождает в пространстве магнитное поле.

Материальные уравнения Уравнения Максвелла не составляют полной системы уравнений электромагнитного поля. Их недостаточно для расчета полей по заданным распределениям зарядов и токов в пространстве Для решения этой задачи необходимо дополнить эту систему уравнений так называемыми материальными уравнениями, которые характеризуют индивидуальные свойства материальной среды, заполняющей пространство.

Материальные уравнения Для изотропных однородных сред, не содержащих сегнетоэлектриков и ферромагнетиков, в случае не слишком сильных электрических и магнитных полей материальные уравнения имеют следующий вид: Здесь и – соответственно электрическая и магнитная проницаемости среды; – удельная электрическая проводимость среды. Из уравнений Максвелла вытекает существование электромагнитных волн, т. е. такого электромагнитного поля, которое способно существовать самостоятельно, в отсутствие электрических зарядов и токов проводимости.