 Лекция 5. Дифракция света (2) § 4. 4. Дифракция Фраунгофера на одной щели. § 4. 5. Количественный критерий для определения вида дифракции. § 5. 3. Дифракционная решетка. § 5. 4. Дифракция на пространственной решетке. Формула Вульфа — Брэггов. § 5. 5. Разрешающая способность оптических приборов.
Лекция 5. Дифракция света (2) § 4. 4. Дифракция Фраунгофера на одной щели. § 4. 5. Количественный критерий для определения вида дифракции. § 5. 3. Дифракционная решетка. § 5. 4. Дифракция на пространственной решетке. Формула Вульфа — Брэггов. § 5. 5. Разрешающая способность оптических приборов.
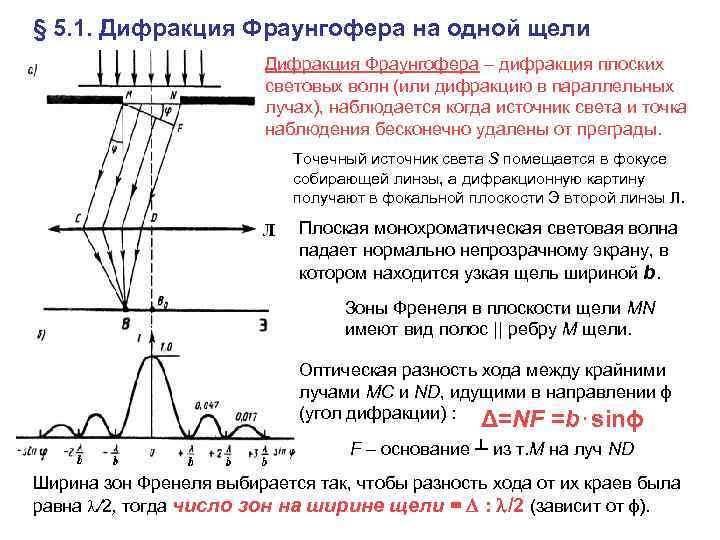 § 5. 1. Дифракция Фраунгофера на одной щели Дифракция Фраунгофера – дифракция плоских световых волн (или дифракцию в параллельных лучах), наблюдается когда источник света и точка наблюдения бесконечно удалены от преграды. Точечный источник света S помещается в фокусе собирающей линзы, а дифракционную картину получают в фокальной плоскости Э второй линзы Л. Плоская монохроматическая световая волна падает нормально непрозрачному экрану, в котором находится узкая щель шириной b. Зоны Френеля в плоскости щели MN имеют вид полос || ребру М щели. Оптическая разность хода между крайними лучами МС и ND, идущими в направлении ϕ (угол дифракции) : Δ=NF =b⋅sinϕ F – основание ┴ из т. М на луч ND Ширина зон Френеля выбирается так, чтобы разность хода от их краев была равна /2, тогда число зон на ширине щели = : /2 (зависит от ϕ).
§ 5. 1. Дифракция Фраунгофера на одной щели Дифракция Фраунгофера – дифракция плоских световых волн (или дифракцию в параллельных лучах), наблюдается когда источник света и точка наблюдения бесконечно удалены от преграды. Точечный источник света S помещается в фокусе собирающей линзы, а дифракционную картину получают в фокальной плоскости Э второй линзы Л. Плоская монохроматическая световая волна падает нормально непрозрачному экрану, в котором находится узкая щель шириной b. Зоны Френеля в плоскости щели MN имеют вид полос || ребру М щели. Оптическая разность хода между крайними лучами МС и ND, идущими в направлении ϕ (угол дифракции) : Δ=NF =b⋅sinϕ F – основание ┴ из т. М на луч ND Ширина зон Френеля выбирается так, чтобы разность хода от их краев была равна /2, тогда число зон на ширине щели = : /2 (зависит от ϕ).
 При дифракции Фраунгофера: все точки волнового фронта в плоскости щели колеблются в одной фазе, амплитуда вторичных волн одинакова для всех зон, не зависит от расстояния до точки наблюдения, коэффициент С(ϕ)=const. Амплитуда результирующих колебаний при интерференции света от каждой пары соседних зон Френеля = 0 (колебания взаимно гасятся). Если число зон Френеля четное Если число зон Френеля нечетное b sin =± 2 m /2 (m= 1, 2, 3, . . . ), b sin =±(2 m+1) /2 (m=1, 2, 3, . . . ), то в точке В наблюдается дифракционный минимум дифракционный максимум, (полная темнота) Амплитуда результирующей волны при угле ϕ: отвечающий действию одной нескомпенсированной зоны Френеля В точке B 0 при ϕ=0 (число зон Френеля =1 )наблюдается центральный дифракционный максимум. Интенсивность света при угле ϕ: Т. к. I−ϕ=I+ϕ, то дифракционная картина симметрична относительно т. В 0.
При дифракции Фраунгофера: все точки волнового фронта в плоскости щели колеблются в одной фазе, амплитуда вторичных волн одинакова для всех зон, не зависит от расстояния до точки наблюдения, коэффициент С(ϕ)=const. Амплитуда результирующих колебаний при интерференции света от каждой пары соседних зон Френеля = 0 (колебания взаимно гасятся). Если число зон Френеля четное Если число зон Френеля нечетное b sin =± 2 m /2 (m= 1, 2, 3, . . . ), b sin =±(2 m+1) /2 (m=1, 2, 3, . . . ), то в точке В наблюдается дифракционный минимум дифракционный максимум, (полная темнота) Амплитуда результирующей волны при угле ϕ: отвечающий действию одной нескомпенсированной зоны Френеля В точке B 0 при ϕ=0 (число зон Френеля =1 )наблюдается центральный дифракционный максимум. Интенсивность света при угле ϕ: Т. к. I−ϕ=I+ϕ, то дифракционная картина симметрична относительно т. В 0.
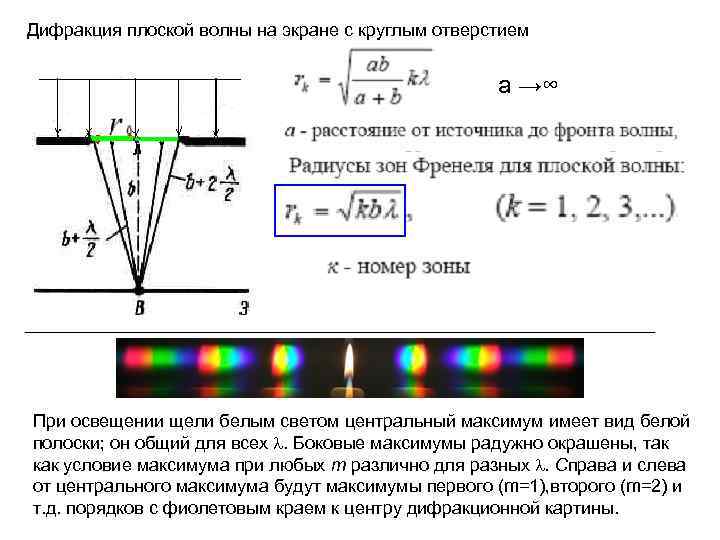 Дифракция плоской волны на экране с круглым отверстием a →∞ При освещении щели белым светом центральный максимум имеет вид белой полоски; он общий для всех . Боковые максимумы радужно окрашены, так как условие максимума при любых т различно для разных . Справа и слева от центрального максимума будут максимумы первого (m=1), второго (m=2) и т. д. порядков с фиолетовым краем к центру дифракционной картины.
Дифракция плоской волны на экране с круглым отверстием a →∞ При освещении щели белым светом центральный максимум имеет вид белой полоски; он общий для всех . Боковые максимумы радужно окрашены, так как условие максимума при любых т различно для разных . Справа и слева от центрального максимума будут максимумы первого (m=1), второго (m=2) и т. д. порядков с фиолетовым краем к центру дифракционной картины.
 § 5. 2. Количественный критерий для определения вида дифракции. Характер дифракционной картины зависит от того, сколько зон Френеля укладывается в отверстии. Определяется значением параметра дифракции ρ, равного отношению размера первой зоны Френеля к размеру отверстия r 0. Радиус первой зоны Френеля равен r 1=√Lλ, тогда ρ=√Lλ /r 0. Различают следующие характерные области дифракции света: ρ<<1 - область геометрической оптики; число зон Френеля, укладывающихся на препятствии, очень большое, дифракция незаметна ρ ~ 1 - область дифракции Френеля ; ρ>>1 - область дифракции Фраунгофера. При фиксированном размере отверстия r 0 и длине падающей волны λ по мере удаления точки наблюдения от отверстия (т. е. с увеличением L) последовательно проходят указанные области.
§ 5. 2. Количественный критерий для определения вида дифракции. Характер дифракционной картины зависит от того, сколько зон Френеля укладывается в отверстии. Определяется значением параметра дифракции ρ, равного отношению размера первой зоны Френеля к размеру отверстия r 0. Радиус первой зоны Френеля равен r 1=√Lλ, тогда ρ=√Lλ /r 0. Различают следующие характерные области дифракции света: ρ<<1 - область геометрической оптики; число зон Френеля, укладывающихся на препятствии, очень большое, дифракция незаметна ρ ~ 1 - область дифракции Френеля ; ρ>>1 - область дифракции Фраунгофера. При фиксированном размере отверстия r 0 и длине падающей волны λ по мере удаления точки наблюдения от отверстия (т. е. с увеличением L) последовательно проходят указанные области.
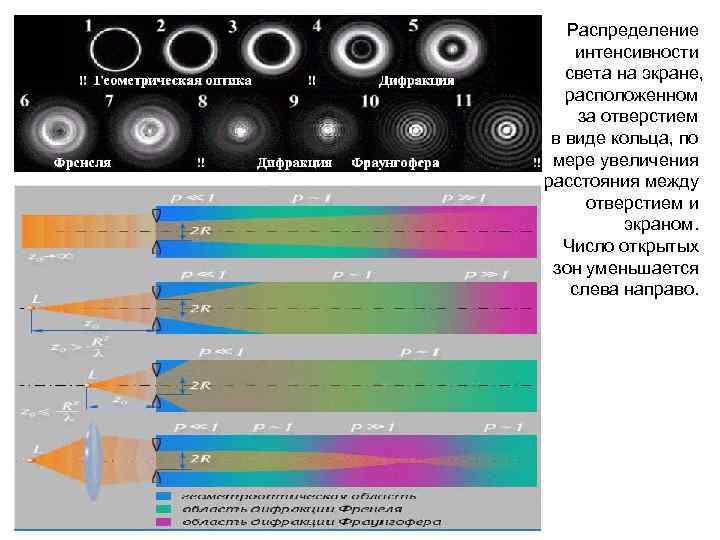 Распределение интенсивности света на экране, расположенном за отверстием в виде кольца, по мере увеличения расстояния между отверстием и экраном. Число открытых зон уменьшается слева направо.
Распределение интенсивности света на экране, расположенном за отверстием в виде кольца, по мере увеличения расстояния между отверстием и экраном. Число открытых зон уменьшается слева направо.
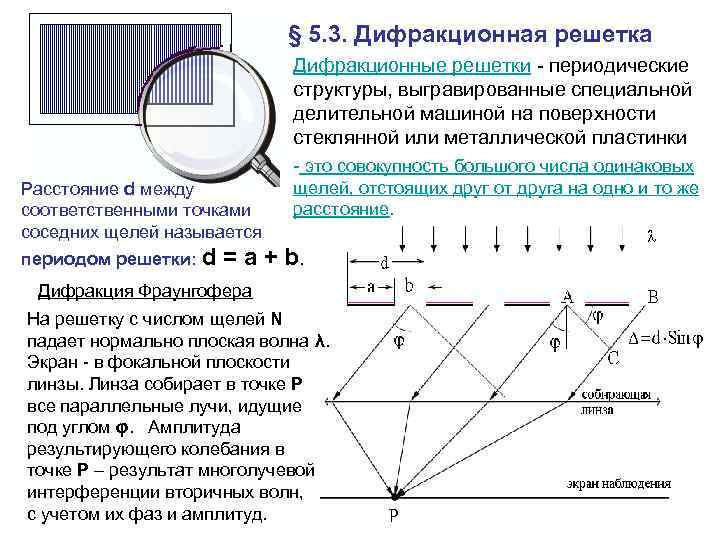 § 5. 3. Дифракционная решетка Дифракционные решетки - периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки Расстояние d между соответственными точками соседних щелей называется - это совокупность большого числа одинаковых щелей, отстоящих друг от друга на одно и то же расстояние. периодом решетки: d = a + b. Дифракция Фраунгофера На решетку с числом щелей N падает нормально плоская волна λ. Экран - в фокальной плоскости линзы. Линза собирает в точке P все параллельные лучи, идущие под углом φ. Амплитуда результирующего колебания в точке P – результат многолучевой интерференции вторичных волн, с учетом их фаз и амплитуд.
§ 5. 3. Дифракционная решетка Дифракционные решетки - периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки Расстояние d между соответственными точками соседних щелей называется - это совокупность большого числа одинаковых щелей, отстоящих друг от друга на одно и то же расстояние. периодом решетки: d = a + b. Дифракция Фраунгофера На решетку с числом щелей N падает нормально плоская волна λ. Экран - в фокальной плоскости линзы. Линза собирает в точке P все параллельные лучи, идущие под углом φ. Амплитуда результирующего колебания в точке P – результат многолучевой интерференции вторичных волн, с учетом их фаз и амплитуд.
 Разность хода лучей, идущих от соответственных точек соседних щелей найдем из треугольника ABC Условия максимума: Условие главного максимума для дифракционной решетки : m = 0, ± 1, ± 2, … Целое число m - порядок дифракционного максимума. В максимуме колебания в точку P будут приходят в одинаковой фазе. Каждая щель создает в Р колебания с амплитудой зависящей от φ: Результирующая амплитуда Aр в P (в главном максимуме) будет в N раз , больше амплитуды от одной щели: Интенсивность в главном максимуме: Зависимость интенсивности дифракционной картины решетки от угла дифракции φ для произвольной точки экрана: I 0 - интенсивность, создаваемая одной щелью при φ = 0 Дифракция от одной щели Интерференция от N щелей
Разность хода лучей, идущих от соответственных точек соседних щелей найдем из треугольника ABC Условия максимума: Условие главного максимума для дифракционной решетки : m = 0, ± 1, ± 2, … Целое число m - порядок дифракционного максимума. В максимуме колебания в точку P будут приходят в одинаковой фазе. Каждая щель создает в Р колебания с амплитудой зависящей от φ: Результирующая амплитуда Aр в P (в главном максимуме) будет в N раз , больше амплитуды от одной щели: Интенсивность в главном максимуме: Зависимость интенсивности дифракционной картины решетки от угла дифракции φ для произвольной точки экрана: I 0 - интенсивность, создаваемая одной щелью при φ = 0 Дифракция от одной щели Интерференция от N щелей
 Минимумы интенсивности дифракционной картины решетки Условия минимумов получаются, если проанализировать на минимум выражение Iр(φ): а) условие минимума для дифракции на щели: б) условие главного минимума для решетки: Колебания от соседних щелей приходят в точку P в противофазе и попарно гасят друга; в) условие добавочных минимумов: k'- целое число не кратное N (при k' кратном N - условие максимума) Чтобы N волн погасили друга, разность фаз должна измениться на 2π/N (соответствующая разность хода - на λ / N) , а не на π, как при интерференции двух волн. Условие для добавочных минимумов, ближайших к главным максимумам порядка m, получим, положив k' = m. N ± 1 : Добавка λ/N дает условие минимума, ближайшего к главному максимуму. Угловую полуширина δθ главных максимумов оценим:
Минимумы интенсивности дифракционной картины решетки Условия минимумов получаются, если проанализировать на минимум выражение Iр(φ): а) условие минимума для дифракции на щели: б) условие главного минимума для решетки: Колебания от соседних щелей приходят в точку P в противофазе и попарно гасят друга; в) условие добавочных минимумов: k'- целое число не кратное N (при k' кратном N - условие максимума) Чтобы N волн погасили друга, разность фаз должна измениться на 2π/N (соответствующая разность хода - на λ / N) , а не на π, как при интерференции двух волн. Условие для добавочных минимумов, ближайших к главным максимумам порядка m, получим, положив k' = m. N ± 1 : Добавка λ/N дает условие минимума, ближайшего к главному максимуму. Угловую полуширина δθ главных максимумов оценим:
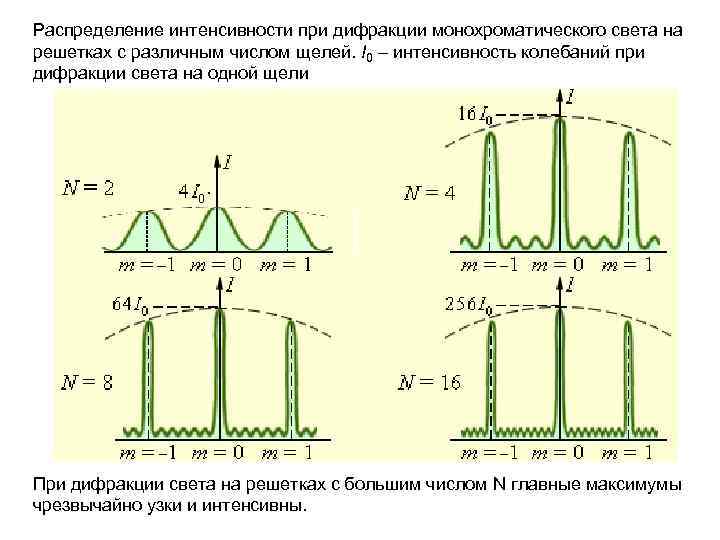 Распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I 0 – интенсивность колебаний при дифракции света на одной щели При дифракции света на решетках с большим числом N главные максимумы чрезвычайно узки и интенсивны.
Распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I 0 – интенсивность колебаний при дифракции света на одной щели При дифракции света на решетках с большим числом N главные максимумы чрезвычайно узки и интенсивны.
 График интенсивности Ip(Sinφ ) N = 4, d = 4 b, а длина волны λ = b/2 интенсивность дифракционной картины от одной щели, помноженная на N 2. Так как модуль sin 1, то из условия главных максимумов следует, что число наблюдаемых главных максимумов m d/. Не все из них реализуются. Исчезают те, положение которых совпадает с минимумами дифракционной картины от одной щели. Sinφ
График интенсивности Ip(Sinφ ) N = 4, d = 4 b, а длина волны λ = b/2 интенсивность дифракционной картины от одной щели, помноженная на N 2. Так как модуль sin 1, то из условия главных максимумов следует, что число наблюдаемых главных максимумов m d/. Не все из них реализуются. Исчезают те, положение которых совпадает с минимумами дифракционной картины от одной щели. Sinφ
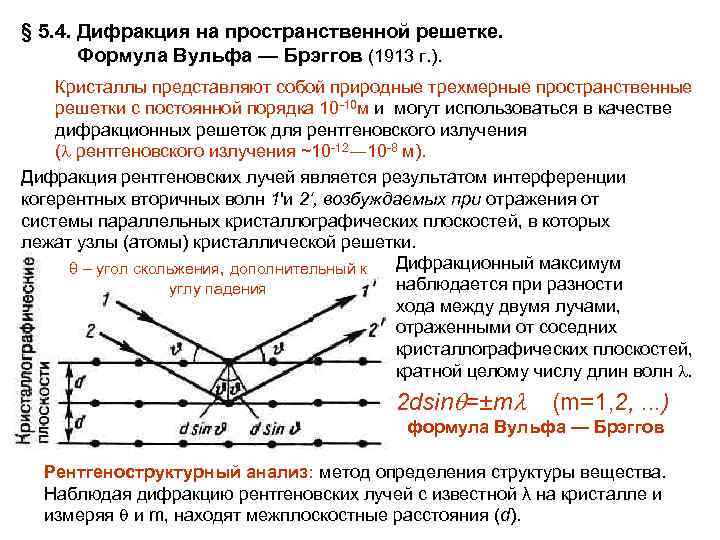 § 5. 4. Дифракция на пространственной решетке. Формула Вульфа — Брэггов (1913 г. ). Кристаллы представляют собой природные трехмерные пространственные решетки с постоянной порядка 10 -10 м и могут использоваться в качестве дифракционных решеток для рентгеновского излучения ( рентгеновского излучения ~10 -12― 10 -8 м). Дифракция рентгеновских лучей является результатом интерференции когерентных вторичных волн 1'и 2‘, возбуждаемых при отражения от системы параллельных кристаллографических плоскостей, в которых лежат узлы (атомы) кристаллической решетки. Дифракционный максимум θ – угол скольжения, дополнительный к наблюдается при разности углу падения хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн . 2 dsin =±m (m=1, 2, . . . ) формула Вульфа — Брэггов Рентгеноструктурный анализ: метод определения структуры вещества. Наблюдая дифракцию рентгеновских лучей с известной λ на кристалле и измеряя и m, находят межплоскостные расстояния (d).
§ 5. 4. Дифракция на пространственной решетке. Формула Вульфа — Брэггов (1913 г. ). Кристаллы представляют собой природные трехмерные пространственные решетки с постоянной порядка 10 -10 м и могут использоваться в качестве дифракционных решеток для рентгеновского излучения ( рентгеновского излучения ~10 -12― 10 -8 м). Дифракция рентгеновских лучей является результатом интерференции когерентных вторичных волн 1'и 2‘, возбуждаемых при отражения от системы параллельных кристаллографических плоскостей, в которых лежат узлы (атомы) кристаллической решетки. Дифракционный максимум θ – угол скольжения, дополнительный к наблюдается при разности углу падения хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн . 2 dsin =±m (m=1, 2, . . . ) формула Вульфа — Брэггов Рентгеноструктурный анализ: метод определения структуры вещества. Наблюдая дифракцию рентгеновских лучей с известной λ на кристалле и измеряя и m, находят межплоскостные расстояния (d).
 § 5. 5. Разрешающая способность оптических приборов Дифракционная решетка и призма являются спектральными приборами Положение главных максимумов (кроме нулевого) зависит от длины волны λ. Решетка способна разлагать излучение в спектр. Если на решетку падает немонохроматическое излучение, то в каждом порядке дифракции (при каждом m) возникает спектр этого излучения. Фиолетовая часть спектра располагается ближе к максимуму 0 порядка. Разложение белого света в спектр с помощью дифракционной решетки Зная постоянную решетки d, измерив на опыте угол φ, отвечающий максимуму порядка m, из условия главного максимума определяют длину волны λ. Если в спектре присутствуют две близкие линии, длины волн которых λ 1 и λ 2 = λ 1 + δλ, то возможность их раздельного восприятия (разрешения) определяется двумя причинами: а) угловым расстоянием между максимумами; б) шириной линий.
§ 5. 5. Разрешающая способность оптических приборов Дифракционная решетка и призма являются спектральными приборами Положение главных максимумов (кроме нулевого) зависит от длины волны λ. Решетка способна разлагать излучение в спектр. Если на решетку падает немонохроматическое излучение, то в каждом порядке дифракции (при каждом m) возникает спектр этого излучения. Фиолетовая часть спектра располагается ближе к максимуму 0 порядка. Разложение белого света в спектр с помощью дифракционной решетки Зная постоянную решетки d, измерив на опыте угол φ, отвечающий максимуму порядка m, из условия главного максимума определяют длину волны λ. Если в спектре присутствуют две близкие линии, длины волн которых λ 1 и λ 2 = λ 1 + δλ, то возможность их раздельного восприятия (разрешения) определяется двумя причинами: а) угловым расстоянием между максимумами; б) шириной линий.
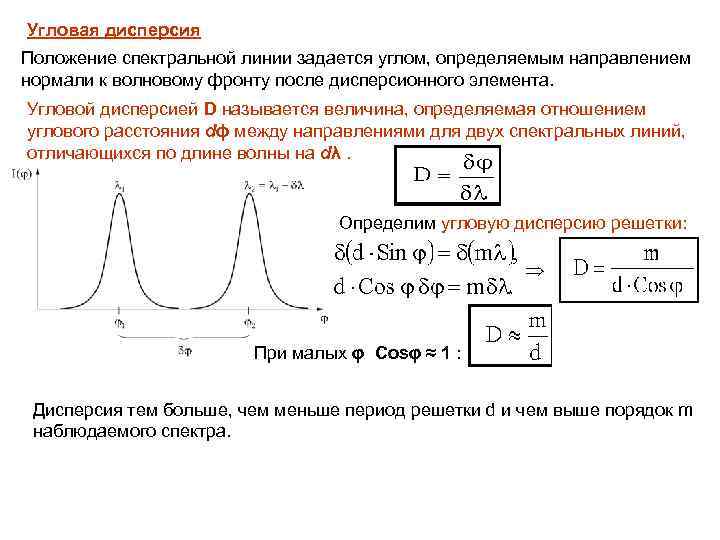 Угловая дисперсия Положение спектральной линии задается углом, определяемым направлением нормали к волновому фронту после дисперсионного элемента. Угловой дисперсией D называется величина, определяемая отношением углового расстояния dϕ между направлениями для двух спектральных линий, отличающихся по длине волны на dλ. Определим угловую дисперсию решетки: При малых φ Cosφ ≈ 1 : Дисперсия тем больше, чем меньше период решетки d и чем выше порядок m наблюдаемого спектра.
Угловая дисперсия Положение спектральной линии задается углом, определяемым направлением нормали к волновому фронту после дисперсионного элемента. Угловой дисперсией D называется величина, определяемая отношением углового расстояния dϕ между направлениями для двух спектральных линий, отличающихся по длине волны на dλ. Определим угловую дисперсию решетки: При малых φ Cosφ ≈ 1 : Дисперсия тем больше, чем меньше период решетки d и чем выше порядок m наблюдаемого спектра.
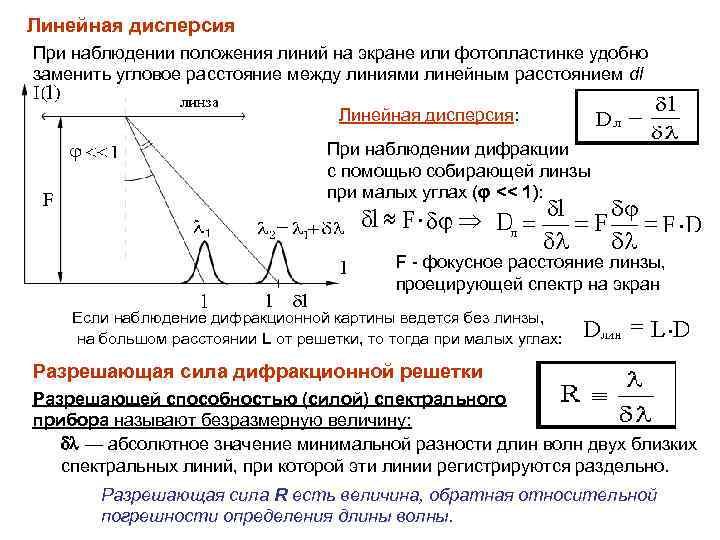 Линейная дисперсия При наблюдении положения линий на экране или фотопластинке удобно заменить угловое расстояние между линиями линейным расстоянием dl Линейная дисперсия: При наблюдении дифракции с помощью собирающей линзы при малых углах (φ << 1): F - фокусное расстояние линзы, проецирующей спектр на экран Если наблюдение дифракционной картины ведется без линзы, на большом расстоянии L от решетки, то тогда при малых углах: Разрешающая сила дифракционной решетки Разрешающей способностью (силой) спектрального прибора называют безразмерную величину: — абсолютное значение минимальной разности длин волн двух близких спектральных линий, при которой эти линии регистрируются раздельно. Разрешающая сила R есть величина, обратная относительной погрешности определения длины волны.
Линейная дисперсия При наблюдении положения линий на экране или фотопластинке удобно заменить угловое расстояние между линиями линейным расстоянием dl Линейная дисперсия: При наблюдении дифракции с помощью собирающей линзы при малых углах (φ << 1): F - фокусное расстояние линзы, проецирующей спектр на экран Если наблюдение дифракционной картины ведется без линзы, на большом расстоянии L от решетки, то тогда при малых углах: Разрешающая сила дифракционной решетки Разрешающей способностью (силой) спектрального прибора называют безразмерную величину: — абсолютное значение минимальной разности длин волн двух близких спектральных линий, при которой эти линии регистрируются раздельно. Разрешающая сила R есть величина, обратная относительной погрешности определения длины волны.
 Критерий Релея: Изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами разрешимы, если центральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого. разрешимы неразрешимы Два близких максимума воспринимаются глазом раздельно, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума. Решетка разрешает 2 линии, если главный максимум линии λ + δλ и добавочный минимум линии λ совпадает, следовательно: N - число щелей, участвующих в образовании главного максимума порядка m. Максимальная разрешающая способность решетки определяется ее общей шириной: Nd – размер решетки, участвующий в образовании максимума mmах
Критерий Релея: Изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами разрешимы, если центральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого. разрешимы неразрешимы Два близких максимума воспринимаются глазом раздельно, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума. Решетка разрешает 2 линии, если главный максимум линии λ + δλ и добавочный минимум линии λ совпадает, следовательно: N - число щелей, участвующих в образовании главного максимума порядка m. Максимальная разрешающая способность решетки определяется ее общей шириной: Nd – размер решетки, участвующий в образовании максимума mmах
 Пример: Решетка имеет период d = 10– 3 мм, ее длина L = 10 см. Тогда, N = 105 (это хорошая решетка). В спектре 2 -го порядка разрешающая способность решетки R = 2· 105. Минимально разрешимый интервал длин волн в зеленой области спектра (λ = 550 нм) равен Δλ = λ / R ≈ 2, 8· 10– 3 нм.
Пример: Решетка имеет период d = 10– 3 мм, ее длина L = 10 см. Тогда, N = 105 (это хорошая решетка). В спектре 2 -го порядка разрешающая способность решетки R = 2· 105. Минимально разрешимый интервал длин волн в зеленой области спектра (λ = 550 нм) равен Δλ = λ / R ≈ 2, 8· 10– 3 нм.


