Лекция 5 Целочисленное программирование Денисова С Т

Лекция 5. Целочисленное программирование • Денисова С. Т. • Старший преподаватель • кафедры ММи. МЭ 1

План: • 1. Постановка задачи целочисленного программирования. • 2. Примеры задач ЦП. • 3 Метод отсекающих плоскостей: метод Гомори • 4. Пример решения задачи методом Гомори.

Задачи ЦЛП • 1) • F(X)= • 3

Задача о назначениях • Задача заключается в наиболее эффективном распределении n работ между n исполнителями. • Пусть Cij – производительность j-исполнителя на i -работе • Введем переменную Xij, которая равна 1, если на i -работу назначен j исполнитель, иначе 0 4

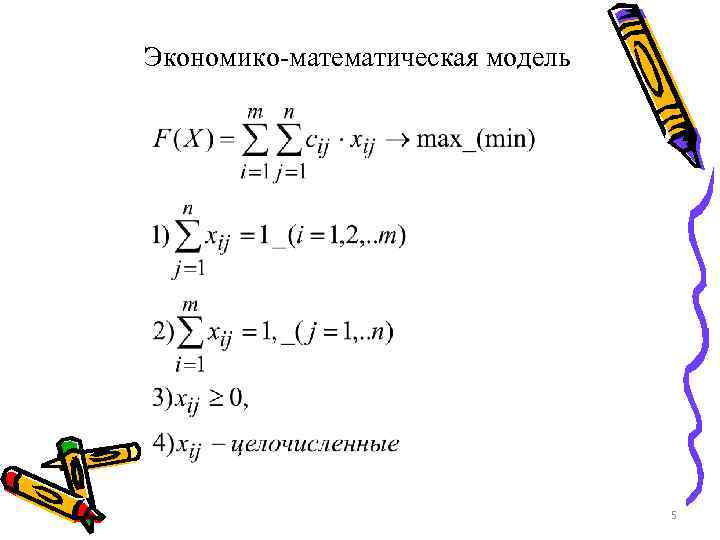Экономико-математическая модель 5

Пример. Задача о трёх станках. 6

Задача о размещениях (размещение m предприятий, определение их производственных мощностей и организации перевозок, чтобы суммарные затраты были бы минимальными)

Задача о коммивояжере: • Имеется n городов, все расстояния между которыми заданы матрицей расстояний С=(Cij ). Коммивояжер выезжает из некоторого города, объезжает все города и возвращается назад. Найти для него кратчайший замкнутый маршрут, проходящий каждый пункт по одному разу. 8

Экономико-математическая модель Введём переменные: 9

Оптимальное исследование рынка • Группе, исследующей рынок, требуется получить данные из n различных мест. В её распоряжении имеется n дней, и она предполагает провести по одному дню в каждом месте, проведя по aj опросов , j=1, 2, . . n. Вероятность успешного опроса в каждом месте задаётся матрицей P. Элемент матрицы Pij характеризует вероятность успешного опроса в течении i –го дня в j-м месте, i=1, 2, . . n. • Определить время проведения опросов, при котором общее число опросов максимально. Сведём данную задачу к задаче о назначениях. 10

Введём величину rij=pij* aj , показывающую число успешных опросов в j-м месте в течение i –го дня. 11

Метод Гомори • 1. Используя симплекс-метод, находим оптимальное решение задачи без учёта требования целочисленности. • 2. Если есть нецелые числа в оптимальном плане, то выбираем среди них решение с наибольшей дробной частью и рассматриваем соответствую-щую ему строку симплекс-таблицы. • Допустим, это строка с номером l. • 12

3. Записываем отсечение (дополнительное ограничение), которое добавляем в симплекстаблицу: 13

4. Используя двойственный симплексный метод , находим оптимальное решение, возвращаемся к пункту 2. • • Пример. f(x 1, x 2)=21 x 1+10 x 2 →max 7 x 1+4 x 2≤ 13 x 1≥ 0, x 2≥ 0 Базис Сi(баз) Опор пл А 1 А 2 А 3 0 13 7 4 1 0 -21 -10 0 14

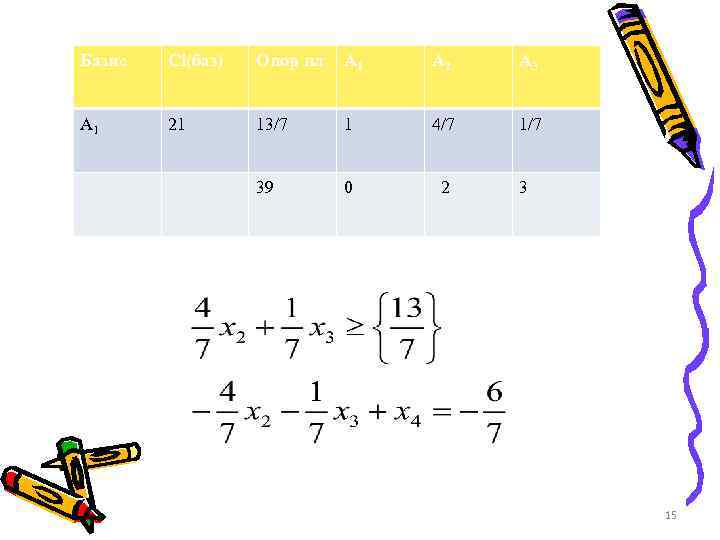Базис Сi(баз) Опор пл А 1 А 2 А 3 А 1 21 13/7 1 4/7 1/7 39 0 2 3 15

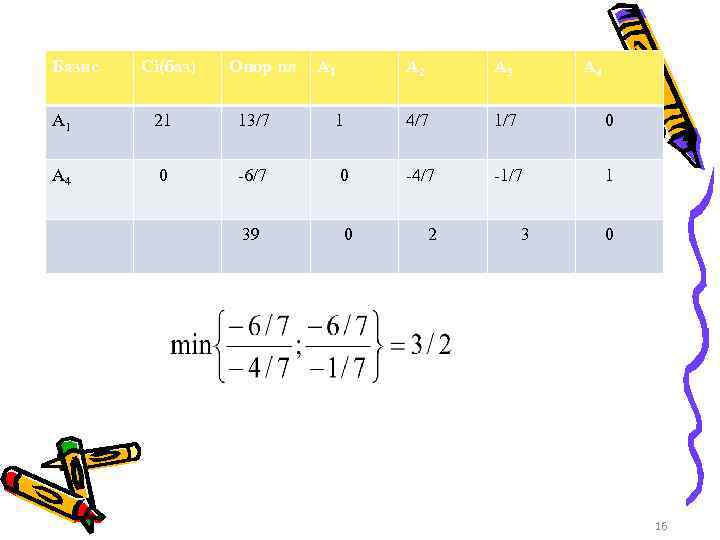Базис Сi(баз) Опор пл А 1 А 2 А 3 А 4 А 1 21 13/7 1 4/7 1/7 0 А 4 0 -6/7 0 -4/7 -1/7 1 39 0 2 3 0 16

Базис Сi(баз) Опор пл А 1 21 1 А 2 10 3/2 36 А 1 А 2 А 3 А 4 1 0 0 1 1/4 -7/4 0 0 5/2 7/2 17

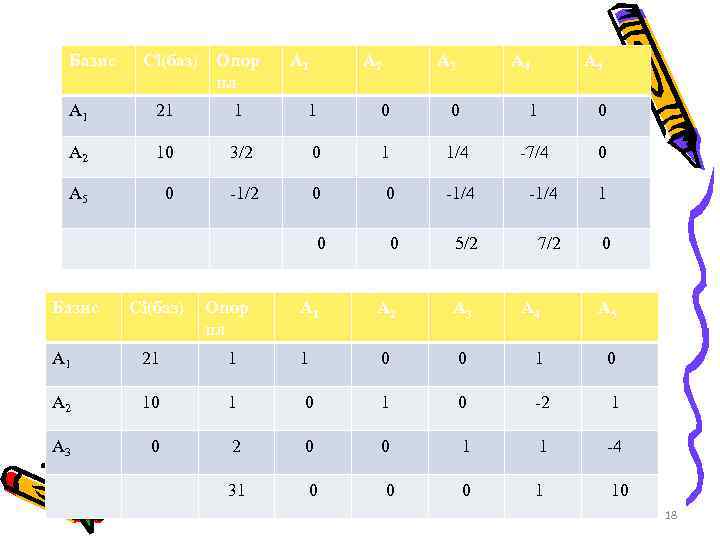Базис Сi(баз) Опор пл А 1 21 1 1 0 0 1 0 А 2 10 3/2 0 1 1/4 -7/4 0 А 5 0 -1/2 0 0 -1/4 1 0 0 5/2 7/2 0 Базис А 1 А 2 А 3 А 4 Сi(баз) Опор пл А 1 А 2 А 3 А 1 21 1 1 0 А 2 10 1 0 А 3 0 2 31 А 5 А 4 А 5 0 1 0 -2 1 0 0 1 1 -4 0 0 0 1 10 18

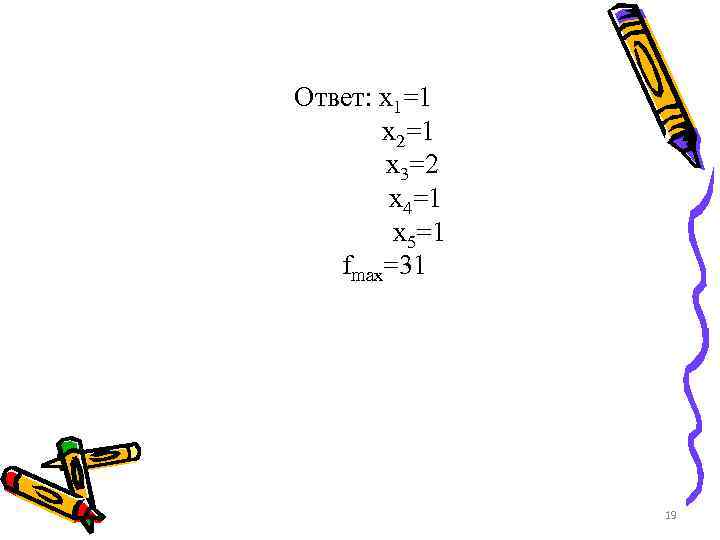Ответ: x 1=1 x 2=1 x 3=2 x 4=1 x 5=1 fmax=31 19