Лекция № 4 Солодухин Е. А.







































ГАУ НГ ЛЕКЦИЯ 4 (поверхность).ppt
- Количество слайдов: 44
 Лекция № 4 Солодухин Е. А. 1
Лекция № 4 Солодухин Е. А. 1
 Поверхность 2
Поверхность 2
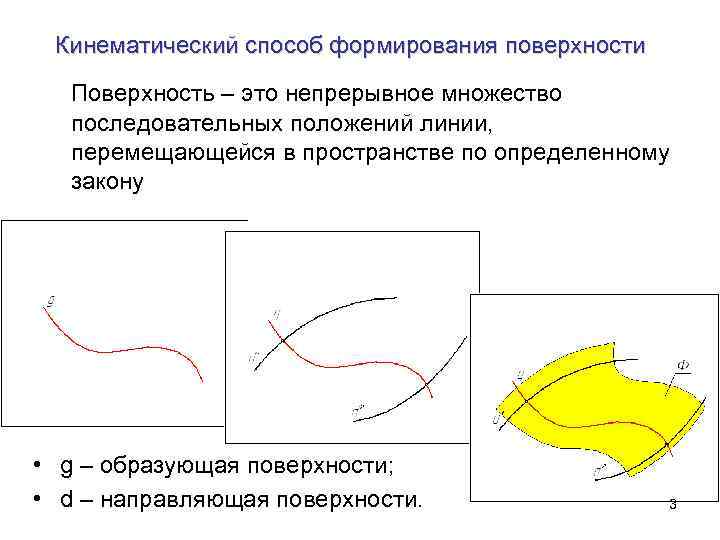
 Кинематический способ формирования поверхности Поверхность – это непрерывное множество последовательных положений линии, перемещающейся в пространстве по определенному закону • g – образующая поверхности; • d – направляющая поверхности. 3
Кинематический способ формирования поверхности Поверхность – это непрерывное множество последовательных положений линии, перемещающейся в пространстве по определенному закону • g – образующая поверхности; • d – направляющая поверхности. 3
 Способы задания поверхности 4
Способы задания поверхности 4
 Определитель поверхности Это совокупность независимых условий, однозначно задающих поверхность. Определитель состоит из двух частей: Ф{(Г)(А)} • Геометрическая (Г) - геометрические фигуры (точки, линии, поверхности), участвующие в образовании поверхности. • Алгоритмическая (А) – закон изменения формы и перемещения образующей. Если образующая является прямой, то ее обозначение выносят за пределы геометрической части Ф{g(Г)(А)} 5
Определитель поверхности Это совокупность независимых условий, однозначно задающих поверхность. Определитель состоит из двух частей: Ф{(Г)(А)} • Геометрическая (Г) - геометрические фигуры (точки, линии, поверхности), участвующие в образовании поверхности. • Алгоритмическая (А) – закон изменения формы и перемещения образующей. Если образующая является прямой, то ее обозначение выносят за пределы геометрической части Ф{g(Г)(А)} 5
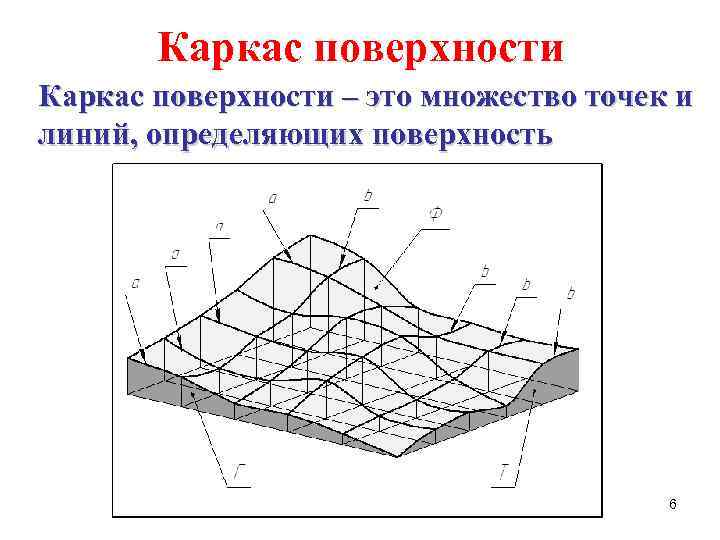
 Каркас поверхности – это множество точек и линий, определяющих поверхность 6
Каркас поверхности – это множество точек и линий, определяющих поверхность 6
 Очерк поверхности ω α = n, ω ∩ П к = n k, Очерк поверхности – это линия пересечения плоскости проекций с проецирующей поверхностью, касательной к заданной поверхности и ее охватывающей. 7
Очерк поверхности ω α = n, ω ∩ П к = n k, Очерк поверхности – это линия пересечения плоскости проекций с проецирующей поверхностью, касательной к заданной поверхности и ее охватывающей. 7
 ПОВЕРХНОСТИ Геометрические Графические Линейчатые Нелинейчатые Образующая - прямая Образующая - кривая Постоянной Три Вращения формы направляющие Переменной Две Винтовые формы направляющие Одна Параллельного направляющая переноса 8
ПОВЕРХНОСТИ Геометрические Графические Линейчатые Нелинейчатые Образующая - прямая Образующая - кривая Постоянной Три Вращения формы направляющие Переменной Две Винтовые формы направляющие Одна Параллельного направляющая переноса 8
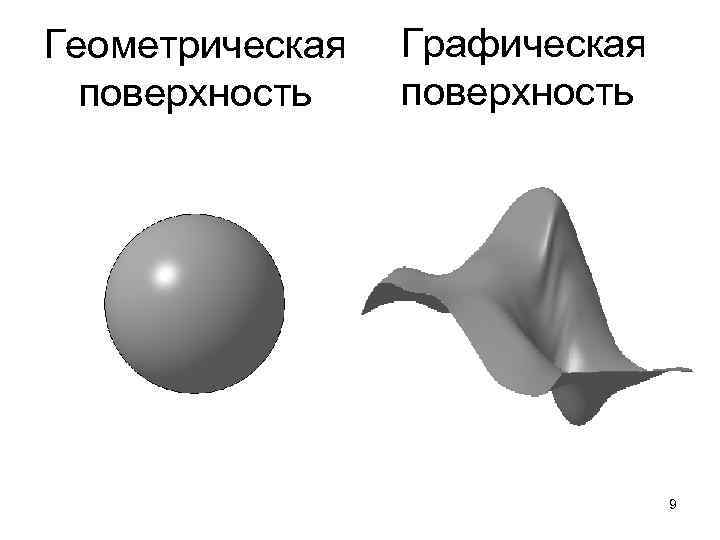
 Геометрическая Графическая поверхность 9
Геометрическая Графическая поверхность 9
 Линейчатые поверхности Образующая поверхности – прямая линия 10
Линейчатые поверхности Образующая поверхности – прямая линия 10
 С тремя направляющими Ф{g(d 1, d 2, d 3)(g∩d 1, g∩d 2, g∩d 3)} Поверхность косого клина косого перехода 11
С тремя направляющими Ф{g(d 1, d 2, d 3)(g∩d 1, g∩d 2, g∩d 3)} Поверхность косого клина косого перехода 11
 С двумя направляющими и плоскостью параллелизма (поверхности Каталана) или с направляющей плоскостью Ф{g(d 1, d 2, )(g∩d 1, g∩d 2, g. II )} 12
С двумя направляющими и плоскостью параллелизма (поверхности Каталана) или с направляющей плоскостью Ф{g(d 1, d 2, )(g∩d 1, g∩d 2, g. II )} 12
 С одной направляющей Торсы Ф{g(d, S)(g∩d, S g)} S – реальная точка S∞ - несобственная точка пространства Ф{g(d, s)(g∩d, g II s)} 13
С одной направляющей Торсы Ф{g(d, S)(g∩d, S g)} S – реальная точка S∞ - несобственная точка пространства Ф{g(d, s)(g∩d, g II s)} 13
 С одной направляющей (Торсы) Плоская поверхность (плоскость) Ф{g(s, d)(g. IIs, g∩d)} Ф{g(S, d)(S g, g∩d)} 14
С одной направляющей (Торсы) Плоская поверхность (плоскость) Ф{g(s, d)(g. IIs, g∩d)} Ф{g(S, d)(S g, g∩d)} 14
 Гранные поверхности Пирамидальная Призматическая 15
Гранные поверхности Пирамидальная Призматическая 15
 Поверхности вращения 16
Поверхности вращения 16
 Основные элементы поверхности вращения 17
Основные элементы поверхности вращения 17
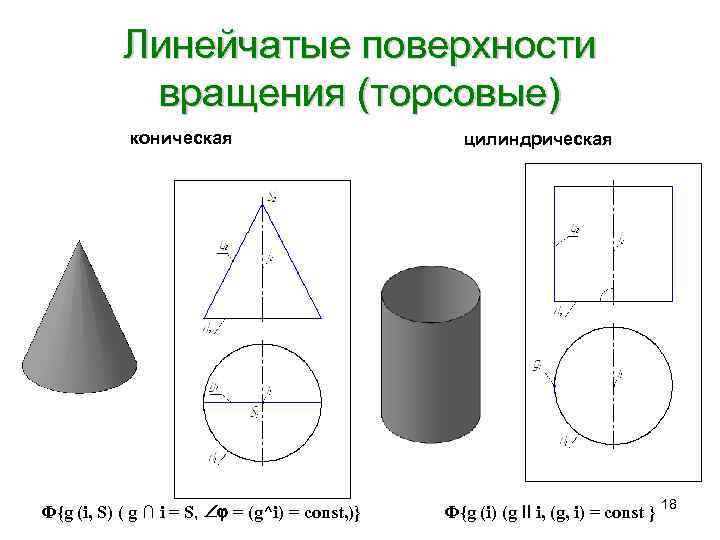
 Линейчатые поверхности вращения (торсовые) коническая цилиндрическая Ф{g (i, S) ( g ∩ i = S, = (g^i) = const, )} Ф{g (i) (g II i, (g, i) = const } 18
Линейчатые поверхности вращения (торсовые) коническая цилиндрическая Ф{g (i, S) ( g ∩ i = S, = (g^i) = const, )} Ф{g (i) (g II i, (g, i) = const } 18
 Нелинейчатые поверхности вращения Гиперболоид вращения 19
Нелинейчатые поверхности вращения Гиперболоид вращения 19
 Винтовые поверхности 20
Винтовые поверхности 20
 Ф{g(d 1, d 2)(g∩d 1, g∩d 2, (g^d 2)=const)} 21
Ф{g(d 1, d 2)(g∩d 1, g∩d 2, (g^d 2)=const)} 21
 Поверхности параллельного переноса 22
Поверхности параллельного переноса 22
 23
23
 Плоскость 24
Плоскость 24
 Способы задания плоскости Σ(m n) Г(А, В, С) Ω(n II m) (ΔABC) Т(А, l ) 25
Способы задания плоскости Σ(m n) Г(А, В, С) Ω(n II m) (ΔABC) Т(А, l ) 25
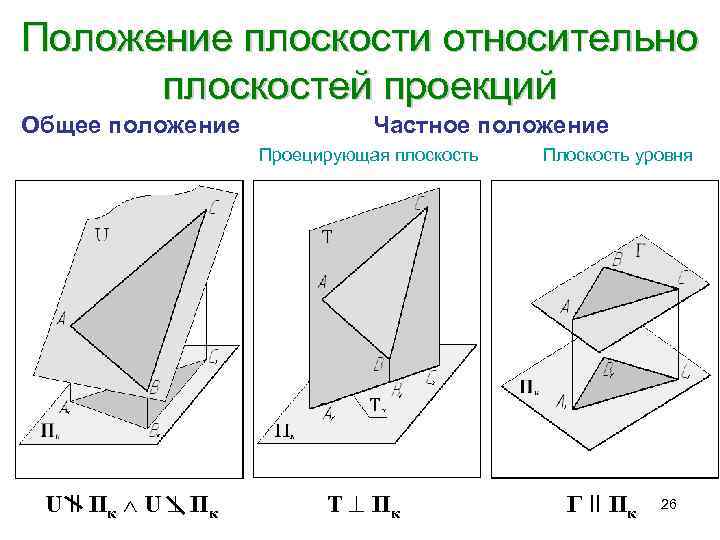
 Положение плоскости относительно плоскостей проекций Общее положение Частное положение Проецирующая плоскость Плоскость уровня U II Пк U Пк Т Пк Г II Пк 26
Положение плоскости относительно плоскостей проекций Общее положение Частное положение Проецирующая плоскость Плоскость уровня U II Пк U Пк Т Пк Г II Пк 26
 ПЛОСКОСТИ ОБЩЕГО ЧАСТНОГО ПОЛОЖЕНИЯ УРОВНЯ ПРОЕЦИРУЮЩИЕ 27
ПЛОСКОСТИ ОБЩЕГО ЧАСТНОГО ПОЛОЖЕНИЯ УРОВНЯ ПРОЕЦИРУЮЩИЕ 27
 Плоскость общего положения 28
Плоскость общего положения 28
 Проецирующие плоскости Горизонтально-проецирующая Фронтально-проецирующая Т П 1 Т П 2 29
Проецирующие плоскости Горизонтально-проецирующая Фронтально-проецирующая Т П 1 Т П 2 29
 Плоскости уровня Горизонтальная плоскость Фронтальная плоскость Г II П 1 Г 2 II x 1, 2 Т II П 2 Т 1 II x 1, 2 30
Плоскости уровня Горизонтальная плоскость Фронтальная плоскость Г II П 1 Г 2 II x 1, 2 Т II П 2 Т 1 II x 1, 2 30
 Прямая в плоскости Плоскость АВС Построить l Выбираем l(1, 2) 1 l 2 l Так как l , то 1 2 Задаем 1 АВ 2 ВС 31
Прямая в плоскости Плоскость АВС Построить l Выбираем l(1, 2) 1 l 2 l Так как l , то 1 2 Задаем 1 АВ 2 ВС 31
 Плоскость АВС Построить l Выбираем l(1, s) 1 l l ||s Так как l , то 1 Задаем 1 АВ s ВС, т. е. l ||ВС 32
Плоскость АВС Построить l Выбираем l(1, s) 1 l l ||s Так как l , то 1 Задаем 1 АВ s ВС, т. е. l ||ВС 32
 Главные линии плоскости К главным линиям плоскости относятся прямые уровня (горизонталь, фронталь, профильная прямая) и линии наибольшего наклона плоскости. 33
Главные линии плоскости К главным линиям плоскости относятся прямые уровня (горизонталь, фронталь, профильная прямая) и линии наибольшего наклона плоскости. 33
 Прямые уровня плоскости 34
Прямые уровня плоскости 34
 Горизонталь плоскости Плоскость АВС Построить h h 1 h 2 x 1, 2 Задаем h(А, 1) 35
Горизонталь плоскости Плоскость АВС Построить h h 1 h 2 x 1, 2 Задаем h(А, 1) 35
 Фронталь плоскости Плоскость АВС Построить f f 2 f 1 x 1, 2 Задаем f(А, 1) 36
Фронталь плоскости Плоскость АВС Построить f f 2 f 1 x 1, 2 Задаем f(А, 1) 36
 Линии наибольшего наклона плоскости Данные линии применяются для определения величины угла наклона плоскости к какой-либо плоскости проекций. В частности, линия наибольшего наклона плоскости, используемая для определения угла наклона к горизонтальной плоскости проекций, получила название линии наибольшего ската плоскости. 37
Линии наибольшего наклона плоскости Данные линии применяются для определения величины угла наклона плоскости к какой-либо плоскости проекций. В частности, линия наибольшего наклона плоскости, используемая для определения угла наклона к горизонтальной плоскости проекций, получила название линии наибольшего ската плоскости. 37
 Линия наибольшего ската плоскости l – линия наибольшего ската плоскости . h- горизонталь плоскости . l h h П 1 l П 1 l 1 h 1 38
Линия наибольшего ската плоскости l – линия наибольшего ската плоскости . h- горизонталь плоскости . l h h П 1 l П 1 l 1 h 1 38
 Плоскость АВС Построить проекции линии наибольшего ската плоскости . Так как l , то задаем l(В, 2) 2 АС Строим l 1 h 1 39
Плоскость АВС Построить проекции линии наибольшего ската плоскости . Так как l , то задаем l(В, 2) 2 АС Строим l 1 h 1 39
 Точка на поверхности 40
Точка на поверхности 40
 Точка принадлежит поверхности, если она принадлежит линии, принадлежащей этой поверхности А Ф А l, l Ф Линия l должна быть плоской и на проекциях иметь наиболее простую геометрическую форму: прямой или окружности (по возможности) 41
Точка принадлежит поверхности, если она принадлежит линии, принадлежащей этой поверхности А Ф А l, l Ф Линия l должна быть плоской и на проекциях иметь наиболее простую геометрическую форму: прямой или окружности (по возможности) 41
 Точка на плоскости На плоскости всегда можно провести прямую либо через две точки, принадлежащие этой плоскости, либо через одну точку, принадлежащую этой плоскости, и параллельно какой-либо прямой, также лежащей в этой плоскости. Следовательно, точка будет принадлежать плоскости, если она будет принадлежать какой-либо прямой, принадлежащей этой плоскости. 42
Точка на плоскости На плоскости всегда можно провести прямую либо через две точки, принадлежащие этой плоскости, либо через одну точку, принадлежащую этой плоскости, и параллельно какой-либо прямой, также лежащей в этой плоскости. Следовательно, точка будет принадлежать плоскости, если она будет принадлежать какой-либо прямой, принадлежащей этой плоскости. 42
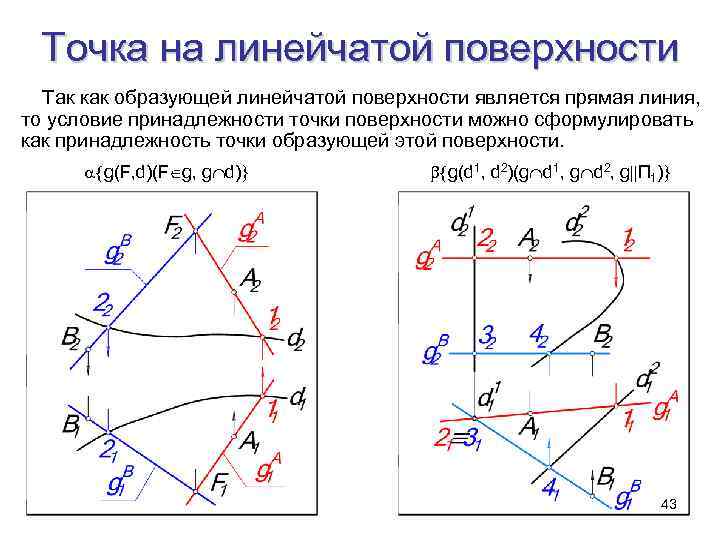
 Точка на линейчатой поверхности Так как образующей линейчатой поверхности является прямая линия, то условие принадлежности точки поверхности можно сформулировать как принадлежность точки образующей этой поверхности. g(F, d)(F g, g d) g(d 1, d 2)(g d 1, g d 2, g П 1) 43
Точка на линейчатой поверхности Так как образующей линейчатой поверхности является прямая линия, то условие принадлежности точки поверхности можно сформулировать как принадлежность точки образующей этой поверхности. g(F, d)(F g, g d) g(d 1, d 2)(g d 1, g d 2, g П 1) 43
 Точка на поверхности вращения Линейчатая поверхность Нелинейчатая поверхность Линия l, которой должна принад- Линия l, которой должна принадлежать точка, может иметь форму как точка, может иметь только форму прямой линии (образующая), так и окружности (параллель). 44
Точка на поверхности вращения Линейчатая поверхность Нелинейчатая поверхность Линия l, которой должна принад- Линия l, которой должна принадлежать точка, может иметь форму как точка, может иметь только форму прямой линии (образующая), так и окружности (параллель). 44

