Лекция 4 Симплекс-метод решение задачи с начальным

Лекция № 4 Симплекс-метод решение задачи с начальным базисом

Условие задачи Предприятие производит полки двух типов (А и Б), объем реализации которых составляет 550 шт. в неделю. Чтобы изготовить одну полку типа А, нужно затратить 2 кв. м материала, а для полки типа Б – 3 кв. м, при этом предприятие может получить не более 1200 кв. м материала в неделю. Для изготовления одной полки типа А требуется 12 мин. станочного времени, а для изготовления одной полки типа В – 30 мин. Станок можно использовать 160 час в неделю. Если прибыль от продажи полки типа А составляет 3 ден. единицы, а от продажи полки типа В – 4 ден. единицы, то сколько полок каждого типа следует выпускать для получения максимальной прибыли?

Условие задачи Пусть предприятие планирует произвести х1 полок типа А и х2 полок типа - В, тогда выручка предприятия Z будет, очевидно, равна Z = 3 х1 +4 Х 2. Величины х1 и х2 по условию применения симплекс метода должны быть неотрицательными, а общие расходы ресурсов при производстве продукции не должны превысить запасы этих ресурсов.

Условие задачи Требуется найти такой план производства, чтобы его выполнение обеспечивало предприятию наибольшую выручку, т. е. Z = 3 х1 +4 Х 2 → MAX при выполнении ограничений: х1 ≥ 0, х2 ≥ 0. Время 60· 160= 9600 мин.

Решение задачи Вначале запишем условие задачи в канонической форме. , то есть ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные : где: Эта система является системой с базисом (базис это величины , каждая из которых входит только в одно уравнение системы с коэффициентом равным единице, х1 и х2 свободные переменные.

Решение задачи Задачи, при решении которых применяется симплекс-метод, должны обладать следующими двумя свойствами: - система ограничений должна быть системой с базисом; - свободные члены всех уравнений в системе должны быть неотрицательны. Полученная нами система – система с базисом и ее свободные члены неотрицательны, следовательно, можно применить симплекс-метод. Составим первую симплекс таблицу (Итерация 0), то есть таблицу коэффициентов переменных целевой функции и системы уравнений.

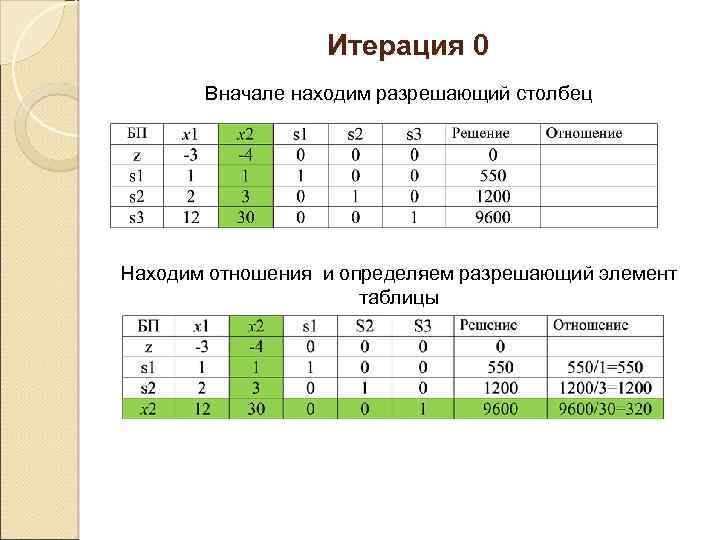Итерация 0 Вначале находим разрешающий столбец Находим отношения и определяем разрешающий элемент таблицы

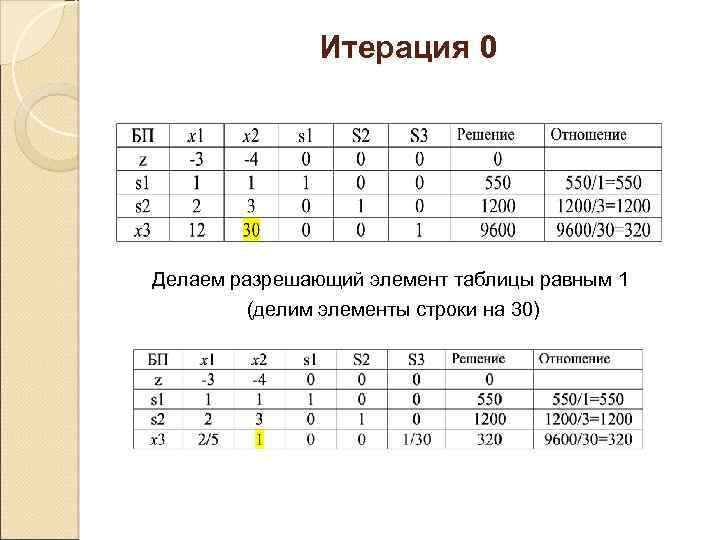Итерация 0 Делаем разрешающий элемент таблицы равным 1 (делим элементы строки на 30)

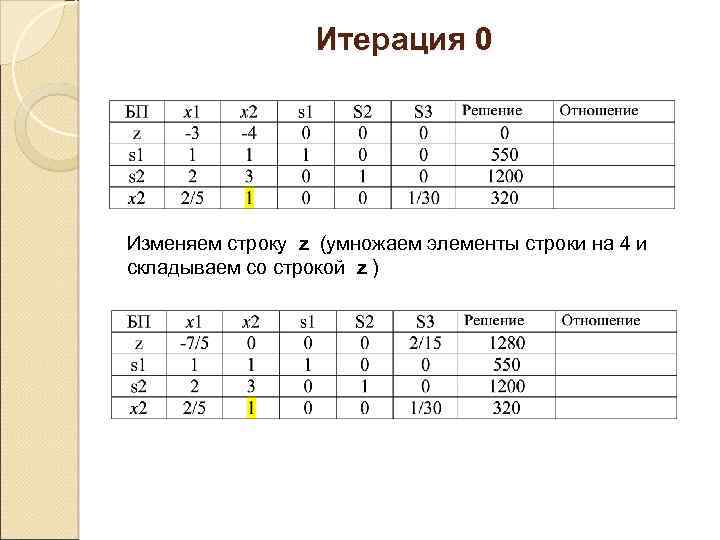Итерация 0 Изменяем строку z (умножаем элементы строки на 4 и складываем со строкой z )

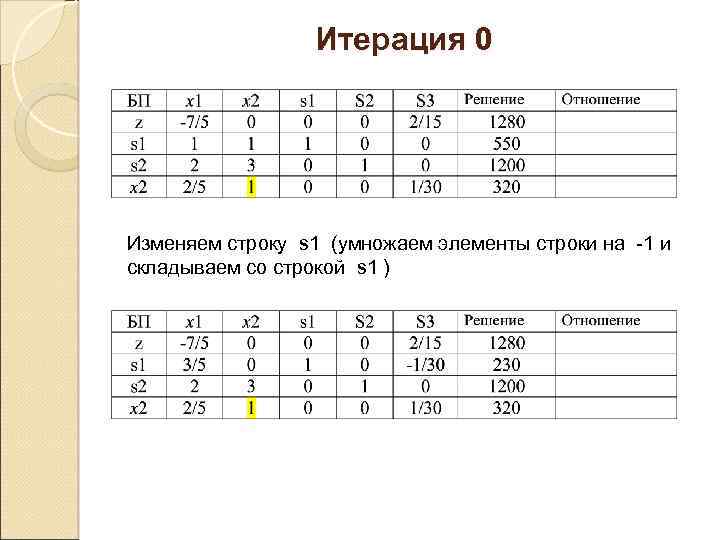Итерация 0 Изменяем строку s 1 (умножаем элементы строки на -1 и складываем со строкой s 1 )

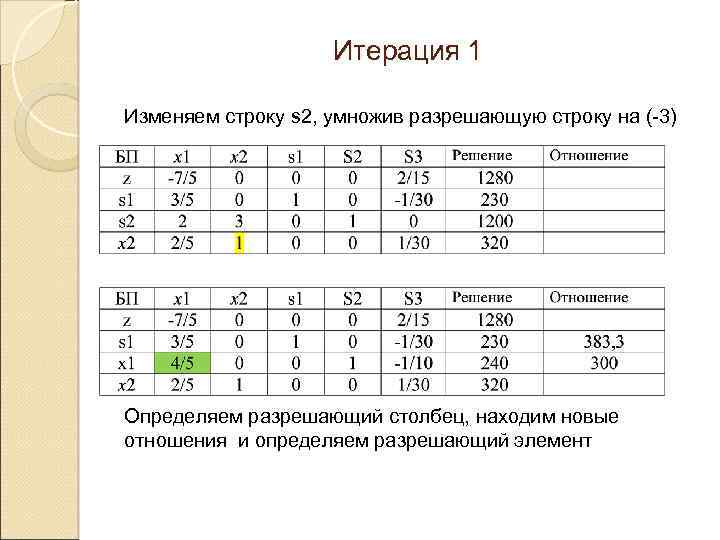Итерация 1 Изменяем строку s 2, умножив разрешающую строку на (-3) Определяем разрешающий столбец, находим новые отношения и определяем разрешающий элемент

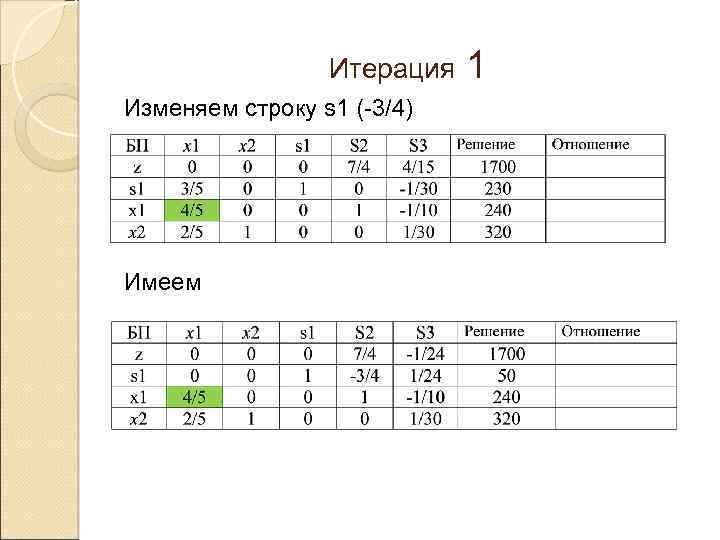Итерация Изменяем строку s 1 (-3/4) Имеем 1

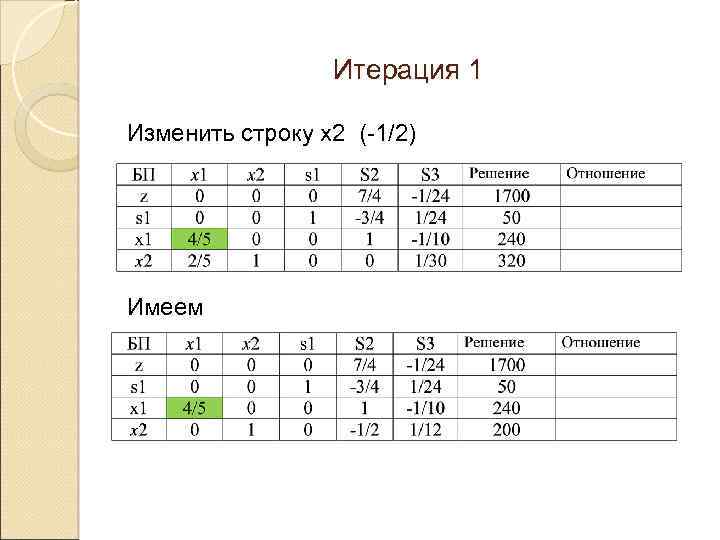Итерация 1 Изменить строку х2 (-1/2) Имеем

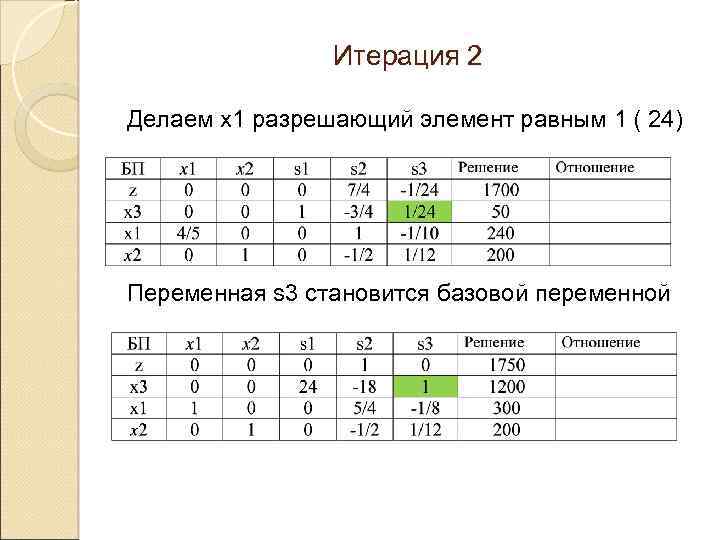Итерация 2 Делаем х1 разрешающий элемент равным 1 ( 24) Переменная s 3 становится базовой переменной

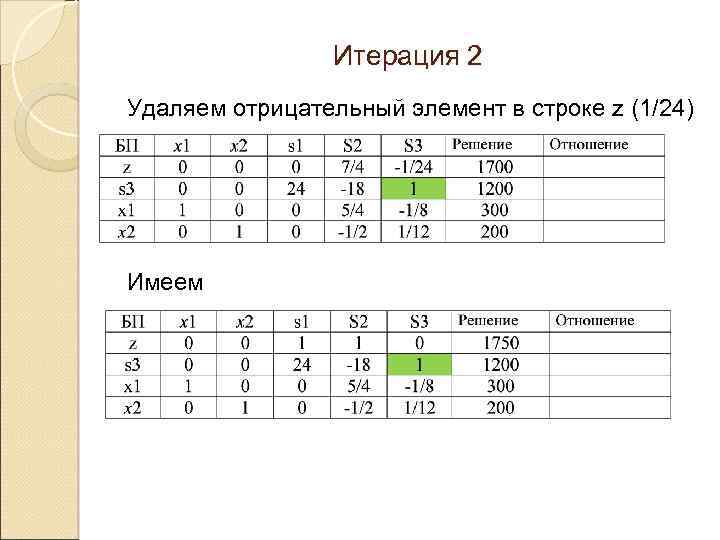Итерация 2 Удаляем отрицательный элемент в строке z (1/24) Имеем

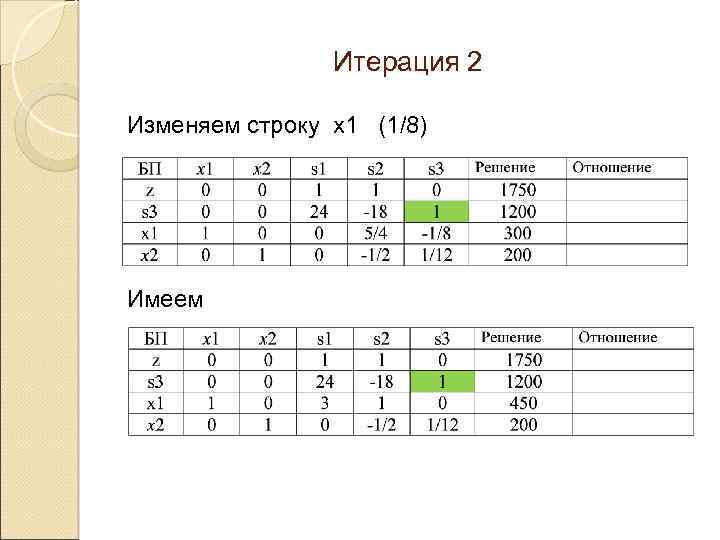Итерация 2 Изменяем строку х1 (1/8) Имеем

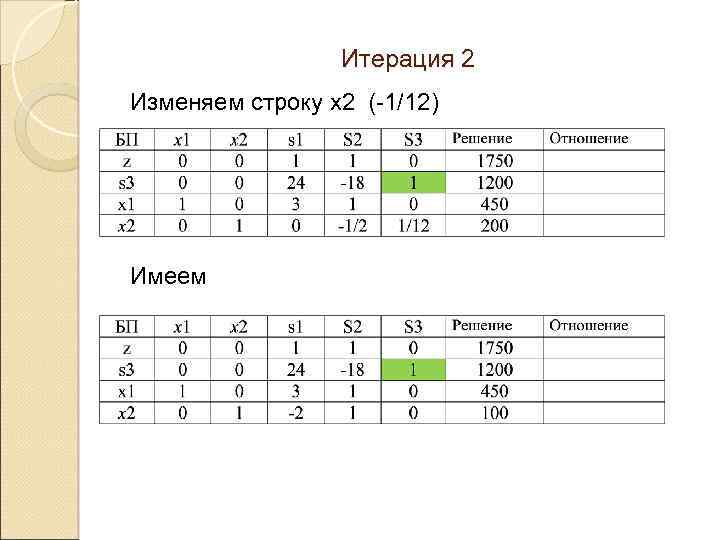Итерация 2 Изменяем строку х2 (-1/12) Имеем

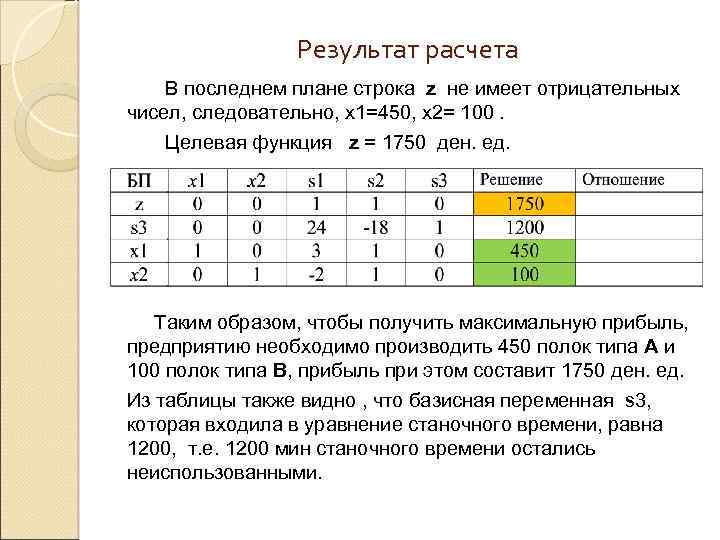Результат расчета В последнем плане строка z не имеет отрицательных чисел, следовательно, х1=450, х2= 100. Целевая функция z = 1750 ден. ед. Таким образом, чтобы получить максимальную прибыль, предприятию необходимо производить 450 полок типа А и 100 полок типа В, прибыль при этом составит 1750 ден. ед. Из таблицы также видно , что базисная переменная s 3, которая входила в уравнение станочного времени, равна 1200, т. е. 1200 мин станочного времени остались неиспользованными.

СПАСИБО ЗА ВНИМАНИЕ!