Лекция 4 Позиционные и
















![[АВ] – натуральная величина (гипотенуза) [АВ] – натуральная величина (гипотенуза)](https://present5.com/presentation/3/-101460997_430255999.pdf-img/-101460997_430255999.pdf-23.jpg)











4. Позиционные и метрические задачи.ppt
- Количество слайдов: 38
 Лекция 4 Позиционные и метрические задачи
Лекция 4 Позиционные и метрические задачи
 1. К позиционным задачам относятся такие задачи, в которых определяется взаимное расположение (позиция) геометрических фигур в пространстве. Основные позиционные задачи: I Пересечение прямой с плоскостью или поверхностью. II Пересечение двух поверхностей или плоскости с поверхностью 2. Для решения позиционных задач используют способ вспомогательных секущих плоскостей или способ конкурирующих линий, который здесь не рассматривается. 3. Алгоритм решения I позиционной задачи: 1) через заданную прямую провести вспомогательную проецирующую плоскость – посредник; 2) построить точку пересечения вспомогательной плоскости с заданной; 3) найти точку, в которой линия пересечения плоскостей пересекает заданную прямую; эта точка и будет искомой; 4) определить видимость прямой линии. 4. Если плоскость или прямая является проецирующей, то на одной из проекций точка уже определена. Остается найти вторую проекцию. 5. Используется метод конкурирующих точек
1. К позиционным задачам относятся такие задачи, в которых определяется взаимное расположение (позиция) геометрических фигур в пространстве. Основные позиционные задачи: I Пересечение прямой с плоскостью или поверхностью. II Пересечение двух поверхностей или плоскости с поверхностью 2. Для решения позиционных задач используют способ вспомогательных секущих плоскостей или способ конкурирующих линий, который здесь не рассматривается. 3. Алгоритм решения I позиционной задачи: 1) через заданную прямую провести вспомогательную проецирующую плоскость – посредник; 2) построить точку пересечения вспомогательной плоскости с заданной; 3) найти точку, в которой линия пересечения плоскостей пересекает заданную прямую; эта точка и будет искомой; 4) определить видимость прямой линии. 4. Если плоскость или прямая является проецирующей, то на одной из проекций точка уже определена. Остается найти вторую проекцию. 5. Используется метод конкурирующих точек
 При решении 1) полной позиционных задач принадлежности: выясняют – точка принадлежит прямой; взаимное – прямая принадлежит расположение (позицию) плоскости; двух и большего числа 2) пересечения: геометрических фигур – прямой с плоскостью, Понятие взаимное поверхностью; расположение включает – двух плоскостей; также принадлежность – плоскости с поверхностью; одной фигуры другой – двух поверхностей; 3) отсутствие При этом возможны случаи: принадлежности: у двух скрещивающихся прямых
При решении 1) полной позиционных задач принадлежности: выясняют – точка принадлежит прямой; взаимное – прямая принадлежит расположение (позицию) плоскости; двух и большего числа 2) пересечения: геометрических фигур – прямой с плоскостью, Понятие взаимное поверхностью; расположение включает – двух плоскостей; также принадлежность – плоскости с поверхностью; одной фигуры другой – двух поверхностей; 3) отсутствие При этом возможны случаи: принадлежности: у двух скрещивающихся прямых
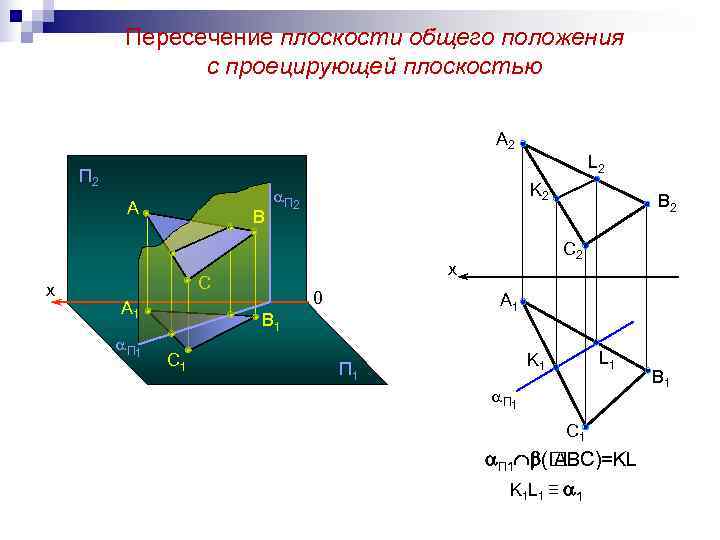
 Пересечение плоскости общего положения с проецирующей плоскостью А 2 L 2 П 2 K 2 A В 2 B С 2 x x C 0 А 1 A 1 B 1 П 1 C 1 K 1 L 1 П 1 В 1 П 1 С 1 П 1 ( АВС)=KL K 1 L 1 ≡ 1
Пересечение плоскости общего положения с проецирующей плоскостью А 2 L 2 П 2 K 2 A В 2 B С 2 x x C 0 А 1 A 1 B 1 П 1 C 1 K 1 L 1 П 1 В 1 П 1 С 1 П 1 ( АВС)=KL K 1 L 1 ≡ 1
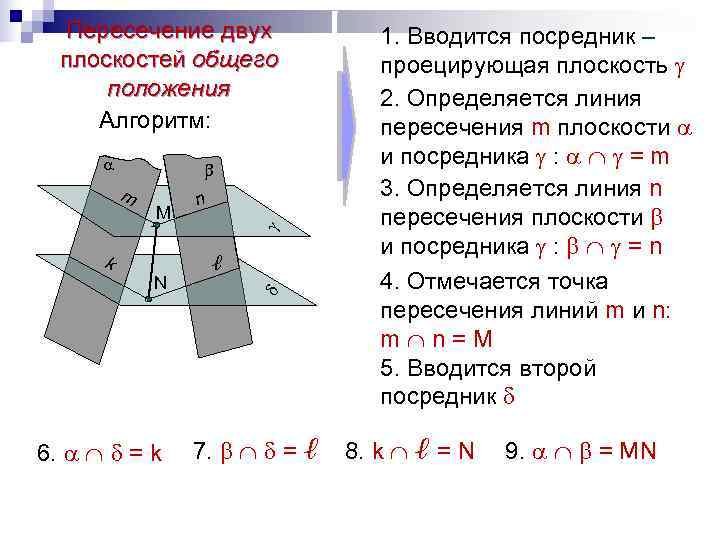
 Пересечение двух 1. Вводится посредник – плоскостей общего проецирующая плоскость положения 2. Определяется линия Алгоритм: пересечения m плоскости и посредника : = m m n 3. Определяется линия n M пересечения плоскости и посредника : = n k ℓ N 4. Отмечается точка пересечения линий m и n: m n=M 5. Вводится второй посредник 6. = k 7. = ℓ 8. k ℓ = N 9. = MN
Пересечение двух 1. Вводится посредник – плоскостей общего проецирующая плоскость положения 2. Определяется линия Алгоритм: пересечения m плоскости и посредника : = m m n 3. Определяется линия n M пересечения плоскости и посредника : = n k ℓ N 4. Отмечается точка пересечения линий m и n: m n=M 5. Вводится второй посредник 6. = k 7. = ℓ 8. k ℓ = N 9. = MN
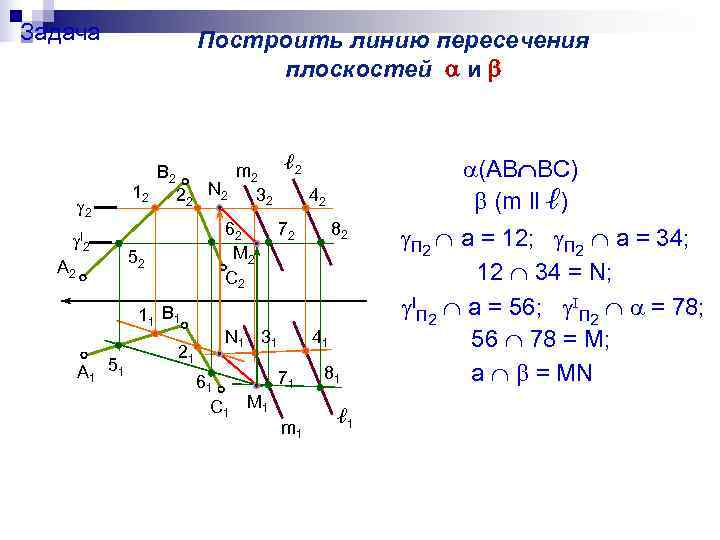
 Задача Построить линию пересечения плоскостей и В 2 m 2 ℓ 2 (AB BC) 12 N 2 22 32 42 (m ll ℓ) 62 72 82 I 2 П 2 a = 12; П 2 a = 34; 52 M 2 А 2 С 2 12 34 = N; 11 В 1 IП 2 a = 56; IП 2 = 78; 21 N 1 31 41 56 78 = M; 51 А 1 61 71 81 а = MN С 1 M 1 ℓ 1 m 1
Задача Построить линию пересечения плоскостей и В 2 m 2 ℓ 2 (AB BC) 12 N 2 22 32 42 (m ll ℓ) 62 72 82 I 2 П 2 a = 12; П 2 a = 34; 52 M 2 А 2 С 2 12 34 = N; 11 В 1 IП 2 a = 56; IП 2 = 78; 21 N 1 31 41 56 78 = M; 51 А 1 61 71 81 а = MN С 1 M 1 ℓ 1 m 1
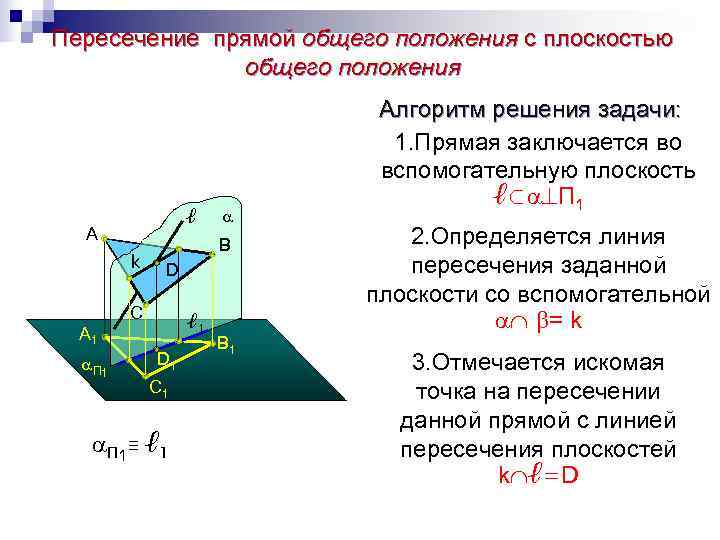
 Пересечение прямой общего положения с плоскостью общего положения Алгоритм решения задачи: 1. Прямая заключается во вспомогательную плоскость ℓ⊂ П 1 ℓ A B 2. Определяется линия k D пересечения заданной плоскости со вспомогательной C = k ℓ 1 A 1 B 1 П 1 D 1 3. Отмечается искомая C 1 точка на пересечении данной прямой с линией П 1 ≡ ℓ 1 пересечения плоскостей k ℓ=D
Пересечение прямой общего положения с плоскостью общего положения Алгоритм решения задачи: 1. Прямая заключается во вспомогательную плоскость ℓ⊂ П 1 ℓ A B 2. Определяется линия k D пересечения заданной плоскости со вспомогательной C = k ℓ 1 A 1 B 1 П 1 D 1 3. Отмечается искомая C 1 точка на пересечении данной прямой с линией П 1 ≡ ℓ 1 пересечения плоскостей k ℓ=D
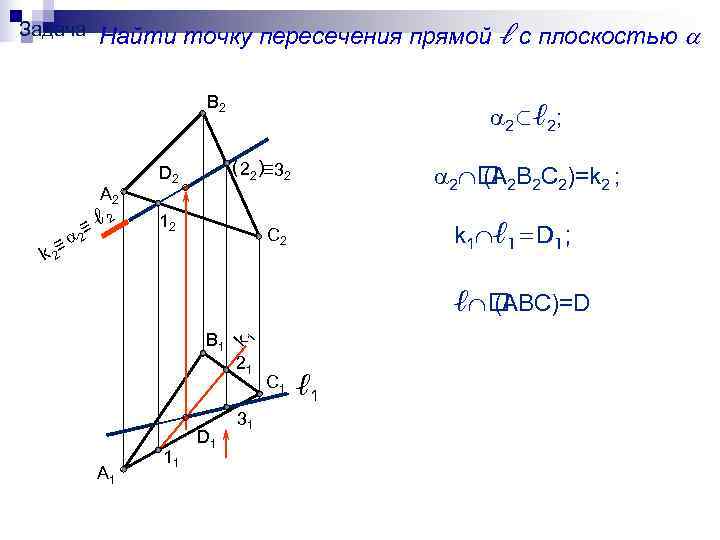
 Задача Найти точку пересечения прямой ℓ с плоскостью В 2 2⊂ℓ 2; ( 22 )≡ 32 D 2 2 2 В 2 С 2)=k 2 ; (А А 2 ≡ℓ 12 2 ≡ 2 С 2 k 1 ℓ 1=D 1; k 2 ℓ (ABC)=D В 1 k 21 С 1 ℓ 1 31 D 1 11 А 1
Задача Найти точку пересечения прямой ℓ с плоскостью В 2 2⊂ℓ 2; ( 22 )≡ 32 D 2 2 2 В 2 С 2)=k 2 ; (А А 2 ≡ℓ 12 2 ≡ 2 С 2 k 1 ℓ 1=D 1; k 2 ℓ (ABC)=D В 1 k 21 С 1 ℓ 1 31 D 1 11 А 1
 Пересечение проецирующей прямой с плоскостью общего положения ℓ 2 В 2 32≡ (42 ) ℓ П 1 12 А 2 D 2 k ℓ ( АВС)=D 22 С 2 В 1 41 С 1 ℓ 1≡D 1≡ 31 11 21 k 1 А 1
Пересечение проецирующей прямой с плоскостью общего положения ℓ 2 В 2 32≡ (42 ) ℓ П 1 12 А 2 D 2 k ℓ ( АВС)=D 22 С 2 В 1 41 С 1 ℓ 1≡D 1≡ 31 11 21 k 1 А 1
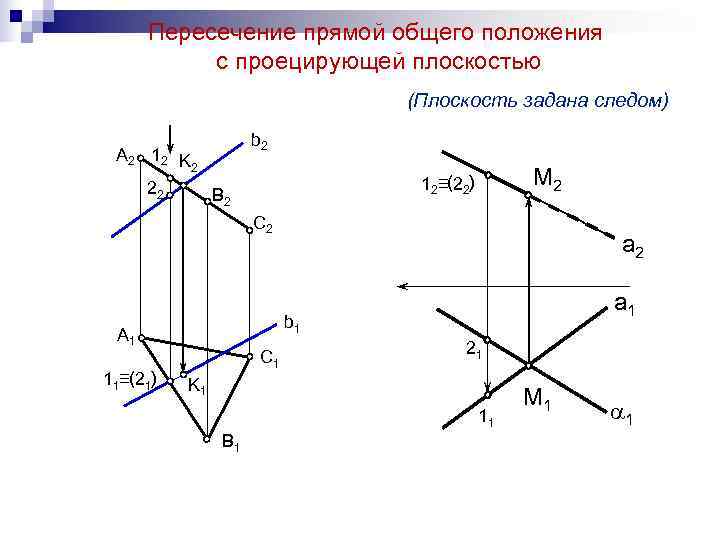
 Пересечение прямой общего положения с проецирующей плоскостью (Плоскость задана следом) b 2 A 2 12 K 2 22 12≡(22) M 2 B 2 C 2 a 1 b 1 A 1 21 C 1 11≡(21) K 1 M 1 11 B 1
Пересечение прямой общего положения с проецирующей плоскостью (Плоскость задана следом) b 2 A 2 12 K 2 22 12≡(22) M 2 B 2 C 2 a 1 b 1 A 1 21 C 1 11≡(21) K 1 M 1 11 B 1
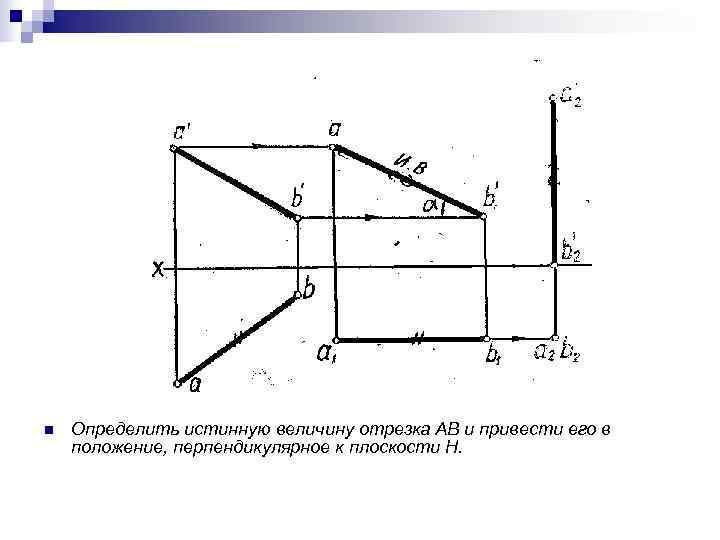
 n Определить истинную величину отрезка АВ и привести его в положение, перпендикулярное к плоскости Н.
n Определить истинную величину отрезка АВ и привести его в положение, перпендикулярное к плоскости Н.
 n Построить в плоскости Р квадрат со стороной, ровной L. Лекция 3. Способы преобразования проекций
n Построить в плоскости Р квадрат со стороной, ровной L. Лекция 3. Способы преобразования проекций
 n В плоскости Р общего положения построить окружность заданного диаметра с центром в точке О. Лекция 3. Способы преобразования проекций
n В плоскости Р общего положения построить окружность заданного диаметра с центром в точке О. Лекция 3. Способы преобразования проекций
 На рисунке плоскость задана треугольником EDK. Определим положение точек М и N относительно плоскости. Сначала определим положение точки М. Проведем в плоскости прямую l, горизонтально конкурирующую с точкой М. Для этого нужно, чтобы на горизонтальной проекции прямая проходила через точку М. А для того, чтобы прямая l принадлежала плоскости, необходимо, чтобы две ее точки принадлежали плоскости (на рисунке это точки Е и 1). Так как и вторая проекция прямой l проходит через проекцию точки М, то точка М принадлежит прямой l, а значит и плоскости. Теперь определим положение точки N относительно той же плоскости треугольника EDK. Для этого проведем на плоскости прямую m, фронтально конкурирующую с точкой N. Прямую m определяют на плоскости точки К и 2. По горизонтальной проекции определяем, что точка N находится вне прямой m, а значит и вне плоскости. Действительно, если бы горизонтальная проекция точки N лежала на прямой m (в месте, отмеченном крестиком), точка принадлежала бы прямой и плоскости. Но так как ее горизонтальная проекция находится ближе, то точка N расположена перед фронтально конкурирующей с ней точкой плоскости, а значит и перед самой плоскостью треугольника EDK.
На рисунке плоскость задана треугольником EDK. Определим положение точек М и N относительно плоскости. Сначала определим положение точки М. Проведем в плоскости прямую l, горизонтально конкурирующую с точкой М. Для этого нужно, чтобы на горизонтальной проекции прямая проходила через точку М. А для того, чтобы прямая l принадлежала плоскости, необходимо, чтобы две ее точки принадлежали плоскости (на рисунке это точки Е и 1). Так как и вторая проекция прямой l проходит через проекцию точки М, то точка М принадлежит прямой l, а значит и плоскости. Теперь определим положение точки N относительно той же плоскости треугольника EDK. Для этого проведем на плоскости прямую m, фронтально конкурирующую с точкой N. Прямую m определяют на плоскости точки К и 2. По горизонтальной проекции определяем, что точка N находится вне прямой m, а значит и вне плоскости. Действительно, если бы горизонтальная проекция точки N лежала на прямой m (в месте, отмеченном крестиком), точка принадлежала бы прямой и плоскости. Но так как ее горизонтальная проекция находится ближе, то точка N расположена перед фронтально конкурирующей с ней точкой плоскости, а значит и перед самой плоскостью треугольника EDK.
 n Нахождение следа прямой
n Нахождение следа прямой
 Определение угла между прямыми
Определение угла между прямыми
 Решения задачи на пересечение прямой и плоскости Даны: прямая а и плоскость α(ΔАВС) 1. Через прямую а проводят фронтально-проецирующую плоскость β (след плоскости показать толстой линией) 2. Плоскость α ∩ β по линии 1 -2 3. Так как прямая а и прямая 1 -2 принадлежат плоскости β , то они пересекаются в точке М, которая и является искомой 4. Для определения видимости воспользуемся точками кажущегося пересечения, которые являются конкурирующими точками. На горизонтальной проекции точками кажущегося пересечения, являются 31 и 31/. Точка 3 принадлежит прямой а, а точка 3/ стороне АС. Судя по фронтальной проекции, точка 3/ расположена выше и на горизонтальной проекции закрывает точку3. Следовательно, прямая проходит на этом участке под плоскостью. 28 На фронтальной проекции точками кажущегося пересечения, являются 22 и 22/. Точка 2 расположена ближе к наблюдателю и на фронтальной проекции закрывает точку 2/, следовательно, прямая на
Решения задачи на пересечение прямой и плоскости Даны: прямая а и плоскость α(ΔАВС) 1. Через прямую а проводят фронтально-проецирующую плоскость β (след плоскости показать толстой линией) 2. Плоскость α ∩ β по линии 1 -2 3. Так как прямая а и прямая 1 -2 принадлежат плоскости β , то они пересекаются в точке М, которая и является искомой 4. Для определения видимости воспользуемся точками кажущегося пересечения, которые являются конкурирующими точками. На горизонтальной проекции точками кажущегося пересечения, являются 31 и 31/. Точка 3 принадлежит прямой а, а точка 3/ стороне АС. Судя по фронтальной проекции, точка 3/ расположена выше и на горизонтальной проекции закрывает точку3. Следовательно, прямая проходит на этом участке под плоскостью. 28 На фронтальной проекции точками кажущегося пересечения, являются 22 и 22/. Точка 2 расположена ближе к наблюдателю и на фронтальной проекции закрывает точку 2/, следовательно, прямая на
 ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА И УГЛОВ ЕГО НАКЛОНА К ПЛОСКОСТЯМ ПРОЕКЦИЙ Задачи, в которых выясняются вопросы измерения длин отрезков и углов, определения натуральной формы плоских фигур и другие называют метрическими задачами. Указанные задачи можно выполнить с помощью способа прямоугольного треугольника. Пусть дан отрезок АВ общего положения в системе двух плоскостей проекций Г и Ф (рисунка). Переместим горизонтальную проекцию отрезка Аг. Вг параллельно самой себе до совмещения точек А и Аг. Рассмотрим полученный треугольник АВВ'. Этот треугольник прямоугольный, поскольку проецирующие лучи перпендикулярны плоскости проекций. Гипотенузой в нем является сам отрезок АВ, один из катетов равен горизонтальной проекции отрезка, а другой катет – разность высот точек А и В (превышение). Угол α, образованный отрезком АВ и катетом, равным его горизонтальной проекции, является углом наклона отрезка АВ к горизонтальной плоскости проекций. Аналогично, перенеся параллельно самой себе фронтальную проекцию отрезка Аф. Вф до совмещения точек А и Аф получим прямоугольный треугольник АВВ". Один из катетов этого треугольника будет равен фронтальной проекции отрезка, а другой – разности глубин одного конца отрезка относительно другого. При этом угол β между гипотенузой АВ и катетом, равным фронтальной проекции отрезка есть угол наклона отрезка к фронтальной плоскости проекций. Таким образом, натуральная величина отрезка является гипотенузой прямоугольного треугольника, у которого одним из катетов будет любая из проекций, а другим катетом соответственно – высота или глубина одного конца отрезка относительно другого. Прямоугольный треугольник с катетами известной величины можно вычертить в любом удобном в конкретной задаче месте чертежа.
ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА И УГЛОВ ЕГО НАКЛОНА К ПЛОСКОСТЯМ ПРОЕКЦИЙ Задачи, в которых выясняются вопросы измерения длин отрезков и углов, определения натуральной формы плоских фигур и другие называют метрическими задачами. Указанные задачи можно выполнить с помощью способа прямоугольного треугольника. Пусть дан отрезок АВ общего положения в системе двух плоскостей проекций Г и Ф (рисунка). Переместим горизонтальную проекцию отрезка Аг. Вг параллельно самой себе до совмещения точек А и Аг. Рассмотрим полученный треугольник АВВ'. Этот треугольник прямоугольный, поскольку проецирующие лучи перпендикулярны плоскости проекций. Гипотенузой в нем является сам отрезок АВ, один из катетов равен горизонтальной проекции отрезка, а другой катет – разность высот точек А и В (превышение). Угол α, образованный отрезком АВ и катетом, равным его горизонтальной проекции, является углом наклона отрезка АВ к горизонтальной плоскости проекций. Аналогично, перенеся параллельно самой себе фронтальную проекцию отрезка Аф. Вф до совмещения точек А и Аф получим прямоугольный треугольник АВВ". Один из катетов этого треугольника будет равен фронтальной проекции отрезка, а другой – разности глубин одного конца отрезка относительно другого. При этом угол β между гипотенузой АВ и катетом, равным фронтальной проекции отрезка есть угол наклона отрезка к фронтальной плоскости проекций. Таким образом, натуральная величина отрезка является гипотенузой прямоугольного треугольника, у которого одним из катетов будет любая из проекций, а другим катетом соответственно – высота или глубина одного конца отрезка относительно другого. Прямоугольный треугольник с катетами известной величины можно вычертить в любом удобном в конкретной задаче месте чертежа.
 Определение расстояния между точкой А и прямой l
Определение расстояния между точкой А и прямой l
 Вращение плоскости вокруг проецирующей прямой Так как плоскость определяется тремя точками, не лежащими на одной прямой, то вращение плоскости сводится к вращению трех точек ее определяющих. На рисунке плоскость Б ( ΔАВС) общего положения повернута вокруг фронтально проецирующей прямой i на угол ω по направлению движения часовой стрелки. Повернув каждую из точек А, В и С на один и тот же угол ω в заданном направлении, получим новые положения точек А 1, В 1 и С 1 определяющих новое положение плоскости после поворота. Поскольку длины отрезков при вращении сохраняются (см. выше), можно повернуть одну из сторон (например АВ) упрощенным Способом, при этом будут построены новые положения сразу двух вершин треугольника – А 1 и В 1. Новое положение третьей вершины можно найти из равенства треугольников ΔАВС=ΔА 1 В 1 С 1 на виде спереди (фронтальной проекции).
Вращение плоскости вокруг проецирующей прямой Так как плоскость определяется тремя точками, не лежащими на одной прямой, то вращение плоскости сводится к вращению трех точек ее определяющих. На рисунке плоскость Б ( ΔАВС) общего положения повернута вокруг фронтально проецирующей прямой i на угол ω по направлению движения часовой стрелки. Повернув каждую из точек А, В и С на один и тот же угол ω в заданном направлении, получим новые положения точек А 1, В 1 и С 1 определяющих новое положение плоскости после поворота. Поскольку длины отрезков при вращении сохраняются (см. выше), можно повернуть одну из сторон (например АВ) упрощенным Способом, при этом будут построены новые положения сразу двух вершин треугольника – А 1 и В 1. Новое положение третьей вершины можно найти из равенства треугольников ΔАВС=ΔА 1 В 1 С 1 на виде спереди (фронтальной проекции).
 n Найти истинную величину треугольника АВС Лекция 3. Способы преобразования проекций
n Найти истинную величину треугольника АВС Лекция 3. Способы преобразования проекций
 A 2 12 C 2 f 2 нв. АВС A 2 C 2 12 j 2 f 2 i 2 B 2 B 2 C 2 // A 1 ≡j 1 C 1 A 1 f 1 // В 1 11 B 1 i 1 C 1
A 2 12 C 2 f 2 нв. АВС A 2 C 2 12 j 2 f 2 i 2 B 2 B 2 C 2 // A 1 ≡j 1 C 1 A 1 f 1 // В 1 11 B 1 i 1 C 1
![> [АВ] – натуральная величина (гипотенуза) > [АВ] – натуральная величина (гипотенуза)](https://present5.com/presentation/3/-101460997_430255999.pdf-img/-101460997_430255999.pdf-23.jpg) [АВ] – натуральная величина (гипотенуза) B 2 нв А B α - угол наклона A 0 z. AB отрезка АВ A 2 к плоскости П 1 х и к проекции А 1 В 1 B 1 z. AB β - угол наклона A 1 нв АB B 0 отрезка АВ к плоскости П 2 и к проекции А 2 В 2
[АВ] – натуральная величина (гипотенуза) B 2 нв А B α - угол наклона A 0 z. AB отрезка АВ A 2 к плоскости П 1 х и к проекции А 1 В 1 B 1 z. AB β - угол наклона A 1 нв АB B 0 отрезка АВ к плоскости П 2 и к проекции А 2 В 2
 Превратить плоскость общего положения Д ( ΔАВС) в проецирующую плоскость (рисунок ). Повернем плоскость Д, например, до положения фронтально проецирующей плоскости. Для этого ее нужно повернуть вокруг горизонтально проецирующей прямой i так, чтобы горизонтали плоскости Д стали фронтально проецирующими прямыми. Поскольку при этом на виде сверху (на горизонтальной проекции) некоторая горизонталь h займет положение h 1, параллельное линиям связи, отсюда определится и угол по- ворота (как угол между «старым» и «новым» положениями горизонтали). Так как ось вращения проходит через одну из вершин треугольника АВС, то на этот угол остается повернуть лишь две оставшиеся вершины – А и С. Новые положения этих вершин А 1 и С 1 совместно с неподвижной вершиной В определят новое фронтально проецирующее положение плоскости Д. Фронтальные проекции точек плоскости Д расположатся на одной прямой, в которую “выродится” плоскость на виде спереди. Угол α между проекцией плоскости Д и прямой перпендикулярной линиям связи – есть натура угла наклона плоскости Д к горизонтальной плоскости проекций. Для поворота плоскости Д до положения горизонтально проецирующей плоскости, нужно за ось вращения принять фронтально проецирующую прямую, проведенную через какую-нибудь точку плоскости.
Превратить плоскость общего положения Д ( ΔАВС) в проецирующую плоскость (рисунок ). Повернем плоскость Д, например, до положения фронтально проецирующей плоскости. Для этого ее нужно повернуть вокруг горизонтально проецирующей прямой i так, чтобы горизонтали плоскости Д стали фронтально проецирующими прямыми. Поскольку при этом на виде сверху (на горизонтальной проекции) некоторая горизонталь h займет положение h 1, параллельное линиям связи, отсюда определится и угол по- ворота (как угол между «старым» и «новым» положениями горизонтали). Так как ось вращения проходит через одну из вершин треугольника АВС, то на этот угол остается повернуть лишь две оставшиеся вершины – А и С. Новые положения этих вершин А 1 и С 1 совместно с неподвижной вершиной В определят новое фронтально проецирующее положение плоскости Д. Фронтальные проекции точек плоскости Д расположатся на одной прямой, в которую “выродится” плоскость на виде спереди. Угол α между проекцией плоскости Д и прямой перпендикулярной линиям связи – есть натура угла наклона плоскости Д к горизонтальной плоскости проекций. Для поворота плоскости Д до положения горизонтально проецирующей плоскости, нужно за ось вращения принять фронтально проецирующую прямую, проведенную через какую-нибудь точку плоскости.
 Вращение плоскости вокруг прямой уровня Как отмечалось выше, основной целью указанного вращения является совмещение с плоскостью уровня. В результате такого совмещения определяется натуральная форма и размеры любой фигуры. Можно так же, построив в данной плоскости фигуру необходимой формы и размеров, «вернуть» ее на основные виды (проекции). Рассмотрим на примере вращение плоскости Б ( ΔАВС) вокруг прямой уровня (в нашем примере горизонтали h) до со вмещения с горизонтальной плоскостью Г (рисунок ). Сначала проведем в данной плоскости горизонталь h, например через точку С и вспомогательную точку 1. При таком выборе оси вращения проекции треугольника «до» и «после» поворота не будут накладываться друг на друга. При вращении точки С и 1, как находящиеся на оси вращения, будут неподвижными. Проведем плоскость Г через горизонталь h и определим совмещенную с ней проекцию точки А. Для этого через горизонтальную проекцию (вид сверху) точки А проведем прямую перпендикулярную горизонтали h. Эта прямая – «вырожденная» проекция плоскости вращения точки А. Отложим от центра вращения О натуральную величину радиуса вращения r, которую предварительно определим с помощью прямоугольного треугольника ОАА*. Для нахождения «совмещенной» проекции точки В нет необходимости находить радиус ее вращения. Она определится в пересечении прямой А 1 -1 с прямой, в которую «вырождается» плоскость вращения точки В на виде сверху. Полученный после совмещения с горизонтальной плоскостью треугольник А 1 В 1 С дает натуральную форму и размеры заданного треугольника АВС. Таким образом, при вращении плоской фигуры вокруг ее прямой уровня для построения «совмещенной» проекции, необходимо определить радиус вращения только одной точки. «Совмещенные» проекции других точек можно построить, используя неподвижные точки прямых, на которых находятся эти точки.
Вращение плоскости вокруг прямой уровня Как отмечалось выше, основной целью указанного вращения является совмещение с плоскостью уровня. В результате такого совмещения определяется натуральная форма и размеры любой фигуры. Можно так же, построив в данной плоскости фигуру необходимой формы и размеров, «вернуть» ее на основные виды (проекции). Рассмотрим на примере вращение плоскости Б ( ΔАВС) вокруг прямой уровня (в нашем примере горизонтали h) до со вмещения с горизонтальной плоскостью Г (рисунок ). Сначала проведем в данной плоскости горизонталь h, например через точку С и вспомогательную точку 1. При таком выборе оси вращения проекции треугольника «до» и «после» поворота не будут накладываться друг на друга. При вращении точки С и 1, как находящиеся на оси вращения, будут неподвижными. Проведем плоскость Г через горизонталь h и определим совмещенную с ней проекцию точки А. Для этого через горизонтальную проекцию (вид сверху) точки А проведем прямую перпендикулярную горизонтали h. Эта прямая – «вырожденная» проекция плоскости вращения точки А. Отложим от центра вращения О натуральную величину радиуса вращения r, которую предварительно определим с помощью прямоугольного треугольника ОАА*. Для нахождения «совмещенной» проекции точки В нет необходимости находить радиус ее вращения. Она определится в пересечении прямой А 1 -1 с прямой, в которую «вырождается» плоскость вращения точки В на виде сверху. Полученный после совмещения с горизонтальной плоскостью треугольник А 1 В 1 С дает натуральную форму и размеры заданного треугольника АВС. Таким образом, при вращении плоской фигуры вокруг ее прямой уровня для построения «совмещенной» проекции, необходимо определить радиус вращения только одной точки. «Совмещенные» проекции других точек можно построить, используя неподвижные точки прямых, на которых находятся эти точки.
 А 2 Заменяемая плоскость z. A s s s s П 2 Х 1, 2 АХ 1, 2 П 1 Рабочая плоскость А 1 АХ 1, 4 П 1 Х 1, 4 П 4 Новая s z. A плоскость А 4 s s
А 2 Заменяемая плоскость z. A s s s s П 2 Х 1, 2 АХ 1, 2 П 1 Рабочая плоскость А 1 АХ 1, 4 П 1 Х 1, 4 П 4 Новая s z. A плоскость А 4 s s
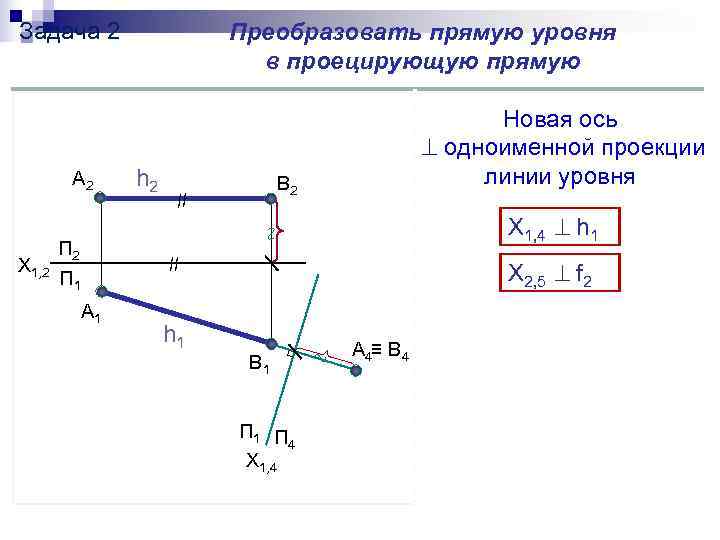
 Задача 2 Преобразовать прямую уровня в проецирующую прямую Новая ось одноименной проекции А 2 h 2 В 2 линии уровня // Х 1, 4 h 1 Х 1, 2 П 2 // ∿ П 1 Х 2, 5 f 2 А 1 h 1 ∿ А 4≡ В 4 В 1 П 1 П 4 Х 1, 4
Задача 2 Преобразовать прямую уровня в проецирующую прямую Новая ось одноименной проекции А 2 h 2 В 2 линии уровня // Х 1, 4 h 1 Х 1, 2 П 2 // ∿ П 1 Х 2, 5 f 2 А 1 h 1 ∿ А 4≡ В 4 В 1 П 1 П 4 Х 1, 4
 Замена плоскостей проекций
Замена плоскостей проекций
 // При переходе к новой системе плоскостей одну из плоскостей заменяют х // так, чтобы геометрический элемент занял частное ая положение а льн Н атур чина и вел Вновь вводимая плоскость должна быть // перпендикулярна оставшейся // плоскости Направление проецирования к новой плоскости должно быть ортогональным Натуральная величина
// При переходе к новой системе плоскостей одну из плоскостей заменяют х // так, чтобы геометрический элемент занял частное ая положение а льн Н атур чина и вел Вновь вводимая плоскость должна быть // перпендикулярна оставшейся // плоскости Направление проецирования к новой плоскости должно быть ортогональным Натуральная величина
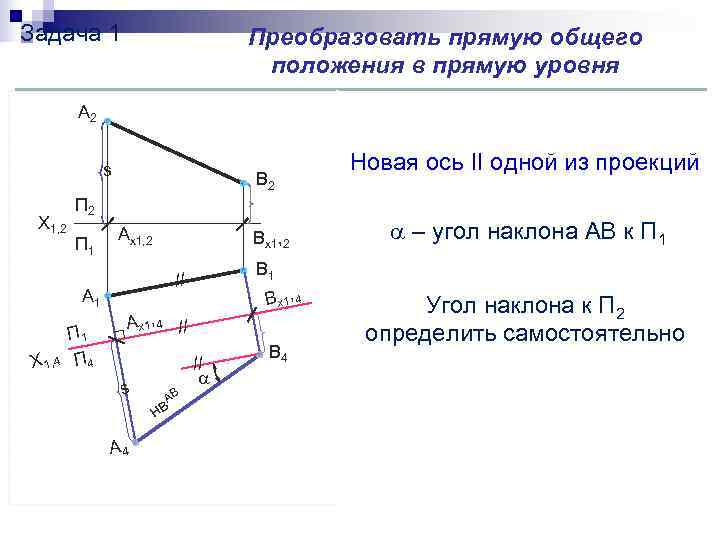
 Задача 1 Преобразовать прямую общего положения в прямую уровня А 2 s Новая ось ІІ одной из проекций В 2 П 2 Х 1, 2 П 1 Ах1, 2 Вх1, 2 – угол наклона АВ к П 1 В 1 // А 1 В х1, 4 Угол наклона к П 2 А х1, 4 // П 1 определить самостоятельно П 4 В 4 Х 1, 4 // s АВ нв А 4
Задача 1 Преобразовать прямую общего положения в прямую уровня А 2 s Новая ось ІІ одной из проекций В 2 П 2 Х 1, 2 П 1 Ах1, 2 Вх1, 2 – угол наклона АВ к П 1 В 1 // А 1 В х1, 4 Угол наклона к П 2 А х1, 4 // П 1 определить самостоятельно П 4 В 4 Х 1, 4 // s АВ нв А 4
 Задача 3 Преобразовать плоскость общего положения в проецирующую плоскость Новая ось В 2 одноименной проекции линии уровня h 2 А 2 С 2 Х 1, 4 h 1 Х 1, 2 П 2 С 4 П 1 С 1 А 4 Х 2, 5 f 2 h 1 А 1 В 4 В 1 П 1 П 4 Х 1, 4
Задача 3 Преобразовать плоскость общего положения в проецирующую плоскость Новая ось В 2 одноименной проекции линии уровня h 2 А 2 С 2 Х 1, 4 h 1 Х 1, 2 П 2 С 4 П 1 С 1 А 4 Х 2, 5 f 2 h 1 А 1 В 4 В 1 П 1 П 4 Х 1, 4
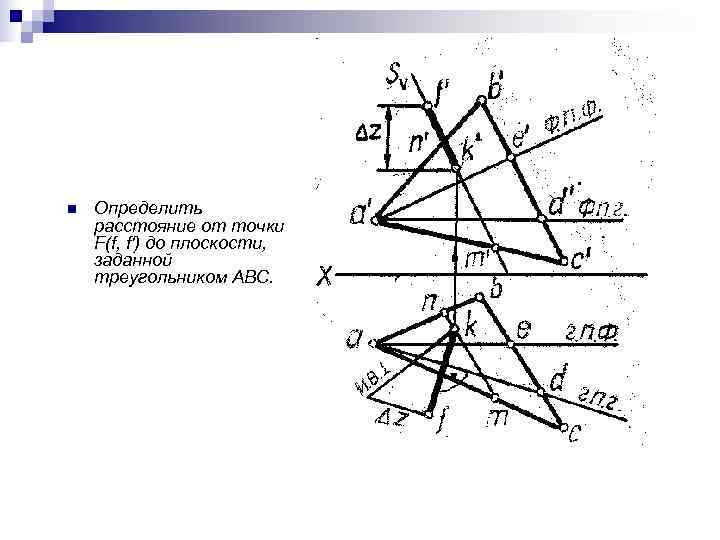
 n Определить расстояние от точки F(f, f') до плоскости, заданной треугольником АВС.
n Определить расстояние от точки F(f, f') до плоскости, заданной треугольником АВС.
 n Способ вращения заключается в том, что данную фигуру вращают в пространстве вокруг некоторой оси до требуемого положения относительно плоскостей проекций. При этом необходимо иметь в виду следующие основные положения, на которых базируется способ вращения: 1) все точки вращаемого геометрического элемента описывают в пространстве дуги окружностей, плоскости которых перпендикулярны к оси вращения. Такая плоскость называется плоскостью вращения точки; 2) центры этих дуг располагаются на оси вращения, а радиусы представляют кратчайшее расстояние от вращаемых точек до оси; 3) точки вращаемого геометрического элемента, лежащие на оси вращения, при вращении не изменяют своего положения в пространстве. Лекция 3. Способы преобразования проекций
n Способ вращения заключается в том, что данную фигуру вращают в пространстве вокруг некоторой оси до требуемого положения относительно плоскостей проекций. При этом необходимо иметь в виду следующие основные положения, на которых базируется способ вращения: 1) все точки вращаемого геометрического элемента описывают в пространстве дуги окружностей, плоскости которых перпендикулярны к оси вращения. Такая плоскость называется плоскостью вращения точки; 2) центры этих дуг располагаются на оси вращения, а радиусы представляют кратчайшее расстояние от вращаемых точек до оси; 3) точки вращаемого геометрического элемента, лежащие на оси вращения, при вращении не изменяют своего положения в пространстве. Лекция 3. Способы преобразования проекций
 Метод замены плоскостей проекций
Метод замены плоскостей проекций
 Задача 4 Преобразовать проецирующую плоскость в плоскость уровня В 5 новая плоскость ll следу Х 5 А 5 нв , 2 П 5 П 2 // С 5 А 2 // В 2 С 2 П 2 Х 2, 1 П 1 А 1 С 1 В 1
Задача 4 Преобразовать проецирующую плоскость в плоскость уровня В 5 новая плоскость ll следу Х 5 А 5 нв , 2 П 5 П 2 // С 5 А 2 // В 2 С 2 П 2 Х 2, 1 П 1 А 1 С 1 В 1
 Нахождение натуральной величины треугольника
Нахождение натуральной величины треугольника
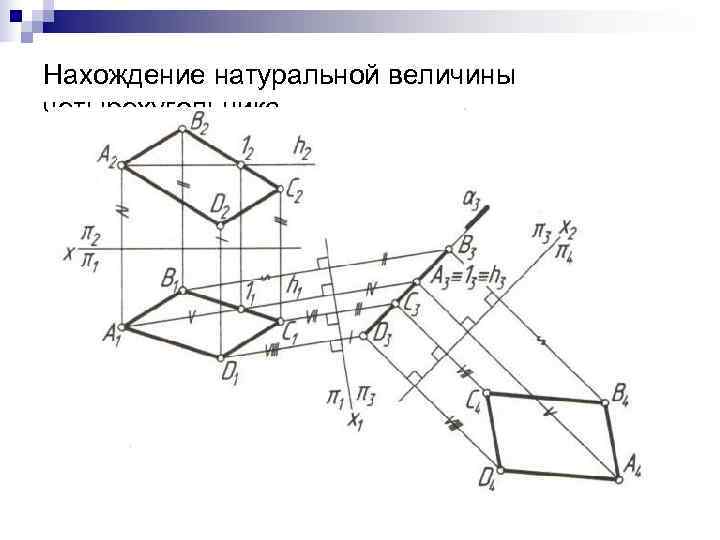
 Нахождение натуральной величины четырехугольника
Нахождение натуральной величины четырехугольника
 1. Какие задачи относятся к позиционным? 2. Какой способ применяют для решения позиционных задач? 3. Из каких этапов состоит решение задачи по определению точки пересечения прямой с плоскостью общего положения? 4. Упрощается ли решение задачи, если плоскость проецирующая? Если прямая проецирующая? 5. Как определяется видимость прямой? 6. Как найти линию пересечения двух плоскостей? 7. В чем состоит сущность способа замены плоскостей проекций? 8. Какие операции необходимо выполнить, чтобы найти натуральную величину плоскости общего положения? 9. В чем состоит суть способа вращения? 10. Как необходимо вращать плоскость общего положения, чтобы преобразовать ее в проецирующую? 11. Как необходимо вращать прямую общего положения, чтобы преобразовать ее в проецирующую? 12. Какие действия необходимо произвести для определения натуральной величины прямой или плоскости? 13. В чем состоит сущность способа замены плоскостей проекций? 14. С какой целью применяют плоско- параллельное перемещение? 15. Какие действия необходимо выполнить, чтобы найти натуральную величину прямой общего положения?
1. Какие задачи относятся к позиционным? 2. Какой способ применяют для решения позиционных задач? 3. Из каких этапов состоит решение задачи по определению точки пересечения прямой с плоскостью общего положения? 4. Упрощается ли решение задачи, если плоскость проецирующая? Если прямая проецирующая? 5. Как определяется видимость прямой? 6. Как найти линию пересечения двух плоскостей? 7. В чем состоит сущность способа замены плоскостей проекций? 8. Какие операции необходимо выполнить, чтобы найти натуральную величину плоскости общего положения? 9. В чем состоит суть способа вращения? 10. Как необходимо вращать плоскость общего положения, чтобы преобразовать ее в проецирующую? 11. Как необходимо вращать прямую общего положения, чтобы преобразовать ее в проецирующую? 12. Какие действия необходимо произвести для определения натуральной величины прямой или плоскости? 13. В чем состоит сущность способа замены плоскостей проекций? 14. С какой целью применяют плоско- параллельное перемещение? 15. Какие действия необходимо выполнить, чтобы найти натуральную величину прямой общего положения?

