Лекция 4 Основные виды логических функций Вопросы 1

Лекция 4 Основные виды логических функций. Вопросы: 1. Диаграммы тактов. 2. Аналитический способ задания логических функций. 3. Последовательностные логические функции.

1. Диаграммы тактов. Диаграмма тактов представляет собой графическое описание условий работы дискретной схемы управления, имеющей, как правило, только один выходной сигнал и конечное количество входных сигналов. Она отражает взаимосвязи входных и выходного сигналов, оговаривает условия и порядок их изменения, является наглядной и удобной формализованной формой записи дискретных алгоритмов управления. Обычно диаграммы тактов составляют перед заполнением таблиц истинности, по ним проверяют полноту и правильность задания алгоритмов управления. На диаграммах тактов (рисунок 1) применяют следующие условные обозначения и ограничения: - каждый такт обозначается кружочком; - значения входных и выходного сигналов записывают в виде дроби, имеющей в числителе строго оговоренную запись последовательности следования значений входных сигналов, а в знаменателе – значения выходного сигнала;

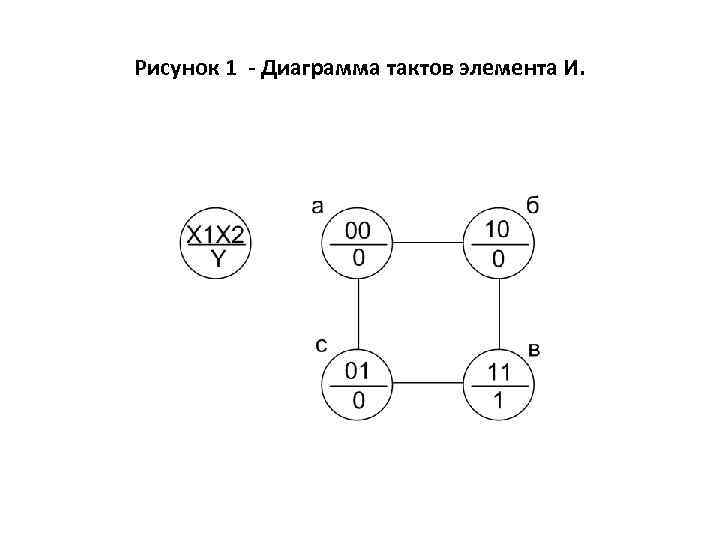Рисунок 1 - Диаграмма тактов элемента И.

- соседними тактами являются лишь те такты, входные комбинации которых отличаются значением только одного сигнала; - графические связи могут быть показаны только между соседними тактами; - графические связи изображаются прямыми линиями со стрелкой или без нее; линии без стрелок разрешают переход между тактами в обоих направлениях при изменении только одного из входных сигналов; линии со стрелкой разрешают переход с такта на такт только по направлению стрелки; - такты, имеющие различные комбинации значений входных сигналов, обозначаются разными буквами без индексов; - такты, имеющие одинаковые комбинации значений входных сигналов, но разные значения выходного сигнала, обозначаются одной и той же буквой, имеющей индексы 0 или 1, соответствующие значению выходного сигнала; - условия порядка следования входных сигналов задаются в виде отдельного такта, находящегося на свободном месте диаграммы.

Пример 1. Управление вытяжными вентиляторами. Технологическое описание процесса. В животноводческом помещении установлено два датчика температуры и один датчик влажности, система микроклимата – вытяжные вентиляторы. Технологические требования – ЭД вентиляторов включаются в тех случаях, когда сигналя от двух любых датчиков превышают заданный уровень, должен быть предусмотрен ручной режим управления ЭД вентиляторов. Словесный алгоритм управления. Эта дискретная система управления имеет три входных сигнала (сигналы от датчиков) и один выходной сигнал (управление ЭД вентиляторов). При превышении заданного уровня появляются сигналы датчиков температуры и влажности. При наличии двух любых или трех сигналов датчиков ЭД вентиляторов включаются в работу, во всех остальных случаях они не работают. Следует предусмотреть режим ручного управления ЭД вентиляторов.

Логические высказывания. Условные обозначения: 0 – отсутствие сигнала; 1 – наличие сигнала; Х 1 – сигнал от датчика температуры № 1; Х 2 – сигнал от датчика температуры № 2; Х 3 – сигнал от датчика влажности; Y – сигнал управления ЭД вентиляторов. Исходное состояние Х 1=0 И Х 2=0 И Х 3=0, Y=0. Если ИЛИ Х 1=1 И Х 2=0 И Х 3=0 ИЛИ Х 1=0 И Х 2=1 И Х 3=0 ИЛИ Х 1=0 И Х 2=0 И Х 3=1, то Y=0. Если Х 1=1 И Х 2=1 И Х 3=0 ИЛИ Х 1=1 И Х 2=0 И Х 3=1 ИЛИ Х 1=0 И Х 2=1 И Х 3=1 ИЛИ Х 1=1 И Х 2=1 И Х 3=1, то Y=1. Формализованная запись алгоритма управления. Согласно составленному сложному высказыванию и с учетом технологических требований изобразим диаграмму тактов – рисунок 2 и таблицу истинности – таблица 1.

Рисунок 2 – Диаграмма тактов для вытяжных вентиляторов. 0

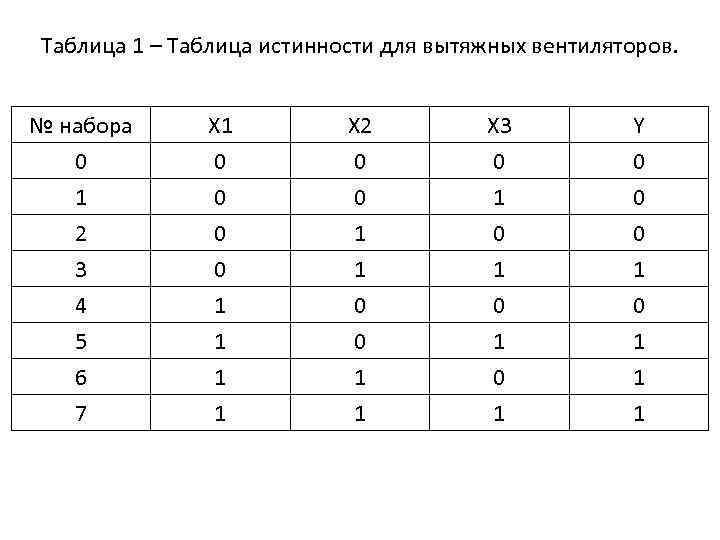Таблица 1 – Таблица истинности для вытяжных вентиляторов. № набора 0 1 2 Х 1 0 0 0 Х 2 0 0 1 Х 3 0 1 0 Y 0 0 0 3 4 5 6 7 0 1 1 1 0 1 1 0 1 1 1

2. Аналитический способ задания логических функций. Это математическая запись логических функций с использованием логических операций НЕ, И, ИЛИ. При этом применяются следующие формы представления логических функций: элементарная дизъюнкция ЭД; элементарная конъюнкция ЭК; дизъюнктивная нормальная форма ДНФ; конъюнктивная нормальная форма КНФ; конституента единицы КЕ; конституента нуля КН; совершенная дизъюнктивная нормальная форма СДНФ; совершенная конъюнктивная нормальная форма СКНФ. ЭД – дизъюнкция любого числа независимых переменных, взятых с инверсией или без нее не более одного раза. Например, Х 1+Х 2; Х 1+Х 2+

ЭК – конъюнкция любого числа независимых переменных, взятых с инверсией или без нее не более одного раза. Например, Х 1∙Х 2; Х 1∙Х 2∙ ДНФ – дизъюнкция любого числа ЭК. Например, Х 1∙Х 2 + Х 1∙Х 2∙ КНФ – конъюнкция любого числа ЭД. Например, (Х 1+Х 2) ∙ ∙(Х 1+Х 2+ ). КЕ – конъюнкция всех переменных данной логической функции, взятых по одной с инверсией или без нее не более одного раза на ее единичном наборе. Если значение переменной на этом наборе равно 1, то она входит в КЕ без инверсии. Если значение переменной на этом наборе равно 0, то она входит в КЕ с инверсией. Например, для таблицы 1 на такте № 6 - Х 1∙Х 2∙ КН – дизъюнкция всех переменных данной логической функции, взятых по одной с инверсией или без нее не более одного раза на ее нулевом наборе. Если значение переменной на этом наборе равно 0, то она входит в КН без инверсии. Если значение переменной на этом наборе равно 1, то она входит в КН с инверсией. Например, для таблицы 1 на такте № 2 - Х 1+Х 2+

СДНФ – дизъюнкция КЕ при всех возможных наборах данной логической функции, где она равна 1. Например, для таблицы 1 получим СКНФ – конъюнкция КН при всех возможных наборах данной логической функции, где она равна 0. Например, для таблицы 1 получим Если требуется получить математическую запись данной логической функции с наименьшим количеством членов, то по ее таблице истинности определяют число значений выходного сигнала, равного 0 и 1. Если число значений, равных 0, больше, чем равных 1, то применяют запись в виде СДНФ, иначе – СКНФ. При одинаковых количествах 0 и 1 число членов как при записи в СДНФ, так и СКНФ будет равное.

3. Последовательностные логические функции. Логические функции, используемые при синтезе дискретных систем управления, подразделяются на комбинационные, последовательностные и временные. Для комбинационных логических функций на всех наборах комбинаций входных сигналов значение выходного сигнала определено однозначно, это или 0 или 1. Все функции, рассмотренные ранее, являлись комбинационными. Для последовательностных логических функций значения выходного сигнала зависят как от комбинации значений входных сигналов, так и от предшествующего значения выходного сигнала. Эта зависимость реализуется в виде сигнала обратной связи, подаваемого, как правило, с выхода схемы на ее вход. Это функции с логической памятью. Сигнал памяти (обратная связь) может поступать на вход схемы не только с ее выхода, но и от промежуточных элементов схемы управления.

Для временных логических функций в число входных переменных входит сигнал времени, т. е алгоритм работы зависит от времени. Время не является двоичной переменной, это непрерывная величина. Эти функции подробно рассмотрим позднее. Признаком последовательностных функций является наличие хотя бы одной пары неоднозначных тактов на диаграмме тактов. В таблице истинности это отражается в виде записи значения выходного сигнала на неоднозначном такте как 0, 1. При алгебраической форме записи алгоритма управления, например, в виде СДНФ, на соответствующем неоднозначном такте в выражении КЕ через символ конъюнкции добавляют выходную переменную без инверсии. Рассмотрим способы представления последовательностых логических функций на примере. Пример 2. Управление вентиляторами. Технологическое описание процесса. В помещении установлено два дискретных датчика температуры с разными порогами срабатывания Т 1>Т 2. Схема должна включать-отключать ЭД вытяжных вентиляторов. Если

сигналы от обоих датчиков превысят установленный уровень, то ЭД вентиляторов включаются и работают до тех пор, пока оба входных сигнала не исчезнут. Словесный алгоритм управления. Схема содержит два входных сигнала (это датчики температуры) и один выходной сигнал (управление ЭД). При превышении температуры уровня уставок на выходе каждого из датчиков появляется сигнал, равный 1. Выходной сигнал схемы будет равен 1 только тогда, когда на ее входе у обоих датчиков сигнал равен 1. Выходной сигнал будет равен 0 только тогда, когда на ее входе у обоих датчиков сигнал равен 0. Логические высказывания. 0 – отсутствие сигнала; 1 - наличие сигнала; Х 1 – сигнал от датчика температуры Т 1; Х 2 – сигнал от датчика температуры Т 2; Y – выходной сигнал управления ЭД вентиляторов.

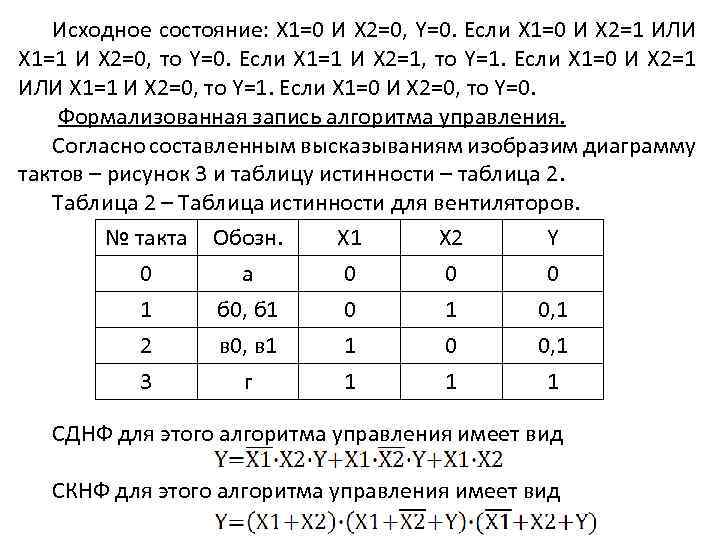Исходное состояние: Х 1=0 И Х 2=0, Y=0. Если Х 1=0 И Х 2=1 ИЛИ Х 1=1 И Х 2=0, то Y=0. Если Х 1=1 И Х 2=1, то Y=1. Если Х 1=0 И Х 2=1 ИЛИ Х 1=1 И Х 2=0, то Y=1. Если Х 1=0 И Х 2=0, то Y=0. Формализованная запись алгоритма управления. Согласно составленным высказываниям изобразим диаграмму тактов – рисунок 3 и таблицу истинности – таблица 2. Таблица 2 – Таблица истинности для вентиляторов. № такта Обозн. Х 1 Х 2 Y 0 а 0 0 0 1 б 0, б 1 0, 1 2 в 0, в 1 1 0 0, 1 3 г 1 1 1 СДНФ для этого алгоритма управления имеет вид СКНФ для этого алгоритма управления имеет вид

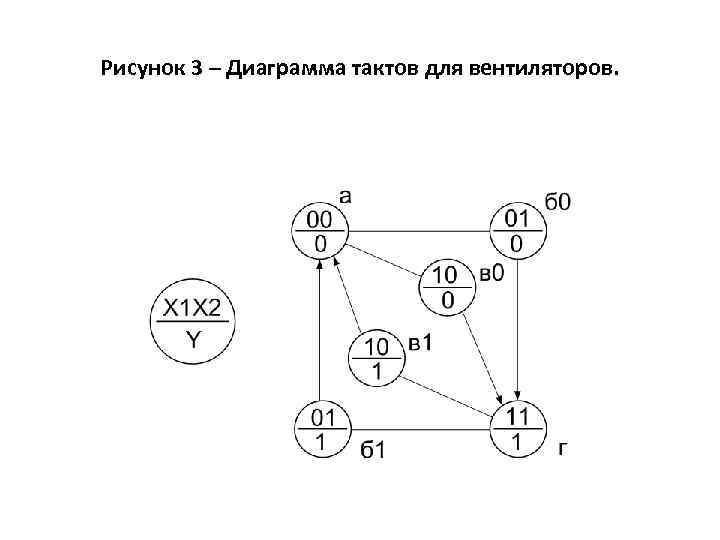Рисунок 3 – Диаграмма тактов для вентиляторов.