Лекция 04, ФЭТП, Тэттэр-Пономарев.ppt
- Количество слайдов: 35
 Лекция 4 Элементы r, L, C, M. Мощность. Энергия. Повторение материала лекций 1 – 3. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
Лекция 4 Элементы r, L, C, M. Мощность. Энергия. Повторение материала лекций 1 – 3. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 Элементы электрических цепей: 2 Пассивные - сопротивление - индуктивность - ёмкость - взаимная индуктивность Активные - источники напряжения (ЭДС)1 - источники тока 1 ЭДС – электродвижущая сила Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
Элементы электрических цепей: 2 Пассивные - сопротивление - индуктивность - ёмкость - взаимная индуктивность Активные - источники напряжения (ЭДС)1 - источники тока 1 ЭДС – электродвижущая сила Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
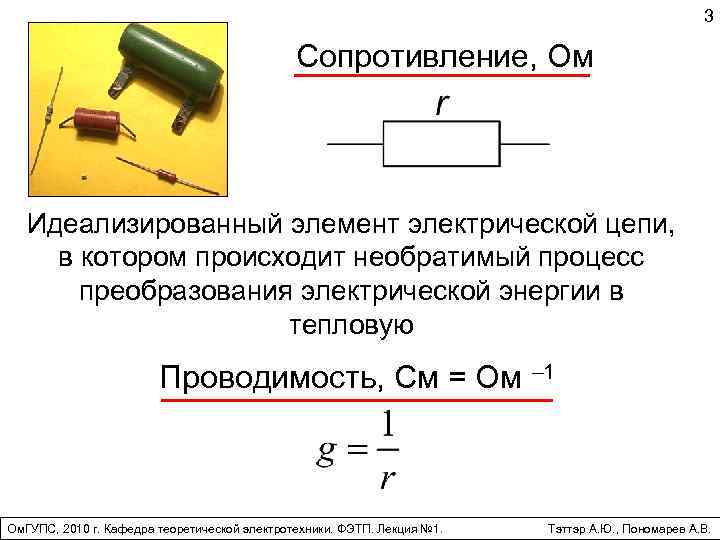 3 Сопротивление, Ом Идеализированный элемент электрической цепи, в котором происходит необратимый процесс преобразования электрической энергии в тепловую Проводимость, См = Ом – 1 Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
3 Сопротивление, Ом Идеализированный элемент электрической цепи, в котором происходит необратимый процесс преобразования электрической энергии в тепловую Проводимость, См = Ом – 1 Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
 4 Закон Ома Георг Симон Ом (1787 – 1854) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
4 Закон Ома Георг Симон Ом (1787 – 1854) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
 5 Мощность, Вт Это скорость поступления энергии от источника в электрическую цепь. Электрическая энергия, Дж при i = I = const P r = U r Ir = r I r 2 W = r I r 2 t Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
5 Мощность, Вт Это скорость поступления энергии от источника в электрическую цепь. Электрическая энергия, Дж при i = I = const P r = U r Ir = r I r 2 W = r I r 2 t Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
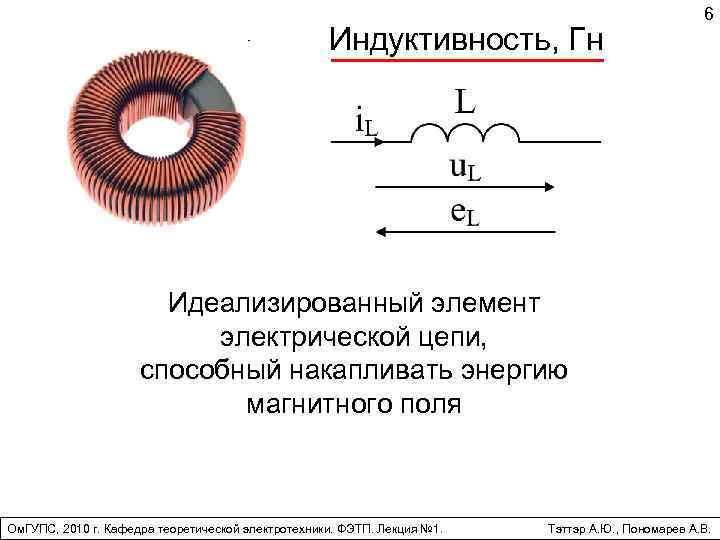 Индуктивность, Гн 6 Идеализированный элемент электрической цепи, способный накапливать энергию магнитного поля Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
Индуктивность, Гн 6 Идеализированный элемент электрической цепи, способный накапливать энергию магнитного поля Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
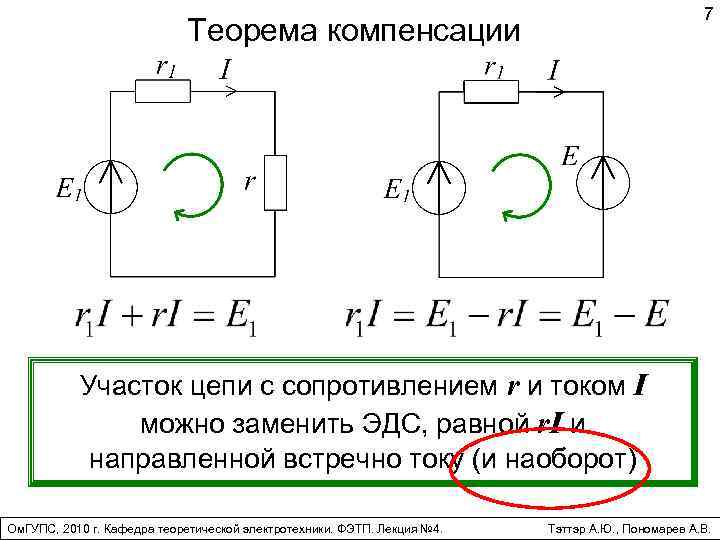 7 Теорема компенсации Участок цепи с сопротивлением r и током I можно заменить ЭДС, равной r. I и направленной встречно току (и наоборот) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
7 Теорема компенсации Участок цепи с сопротивлением r и током I можно заменить ЭДС, равной r. I и направленной встречно току (и наоборот) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
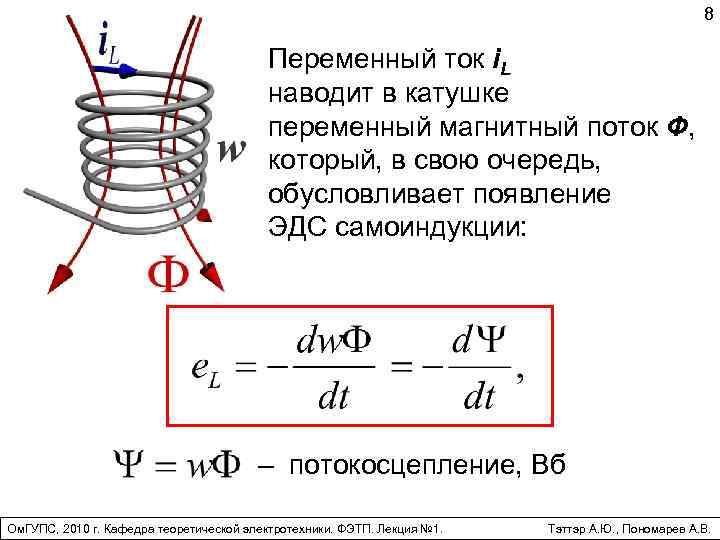 8 Переменный ток i. L наводит в катушке переменный магнитный поток Ф, который, в свою очередь, обусловливает появление ЭДС самоиндукции: – потокосцепление, Вб Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
8 Переменный ток i. L наводит в катушке переменный магнитный поток Ф, который, в свою очередь, обусловливает появление ЭДС самоиндукции: – потокосцепление, Вб Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
 Потокосцепление и ток связаны соотношением: 9 При постоянной L: Падение напряжения на индуктивности u. L равно по величине e. L и противоположно по знаку: При постоянном токе напряжение на индуктивности равно нулю. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
Потокосцепление и ток связаны соотношением: 9 При постоянной L: Падение напряжения на индуктивности u. L равно по величине e. L и противоположно по знаку: При постоянном токе напряжение на индуктивности равно нулю. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 10 Мощность Энергия магнитного поля в индуктивности: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
10 Мощность Энергия магнитного поля в индуктивности: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 11 Емкость, Ф Идеализированный элемент электрической цепи, накапливающий энергию электрического поля Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
11 Емкость, Ф Идеализированный элемент электрической цепи, накапливающий энергию электрического поля Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
 Ток в емкости определяется количеством заряда в единицу времени: 12 q – Кл Заряд и напряжение на емкости связаны соотношением: При постоянной C: При постоянном напряжении ток в емкости равен нулю Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
Ток в емкости определяется количеством заряда в единицу времени: 12 q – Кл Заряд и напряжение на емкости связаны соотношением: При постоянной C: При постоянном напряжении ток в емкости равен нулю Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 13 Мощность Энергия электрического поля емкости: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
13 Мощность Энергия электрического поля емкости: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
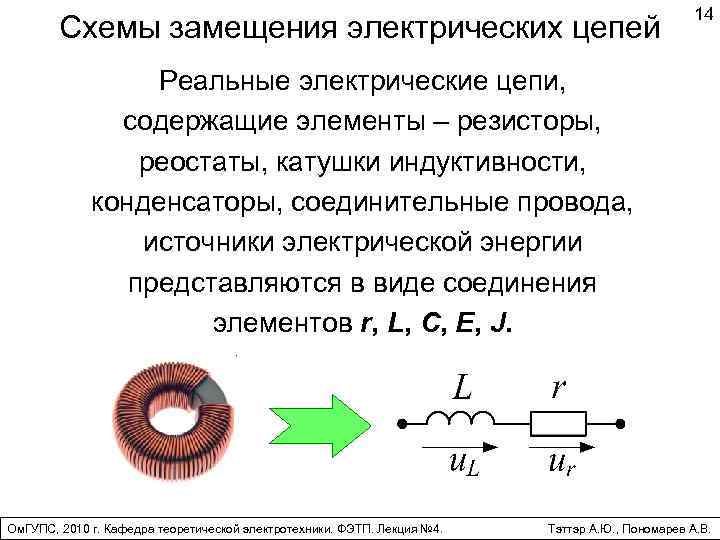 Схемы замещения электрических цепей 14 Реальные электрические цепи, содержащие элементы – резисторы, реостаты, катушки индуктивности, конденсаторы, соединительные провода, источники электрической энергии представляются в виде соединения элементов r, L, C, E, J. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
Схемы замещения электрических цепей 14 Реальные электрические цепи, содержащие элементы – резисторы, реостаты, катушки индуктивности, конденсаторы, соединительные провода, источники электрической энергии представляются в виде соединения элементов r, L, C, E, J. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 15 Находящие широкое применение различные трансформаторы характеризуются кроме указанных еще одним параметром – взаимной индуктивностью M, которая характеризует степень магнитной связи между его обмотками. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
15 Находящие широкое применение различные трансформаторы характеризуются кроме указанных еще одним параметром – взаимной индуктивностью M, которая характеризует степень магнитной связи между его обмотками. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 16 В состав цепей постоянного тока входят: – E, J (источники напряжения и тока); – r (сопротивления). Элементы электрических цепей соединяются последовательно и параллельно. Законы Кирхгофа являются основой различных способов расчета электрических цепей. Многие частные задачи можно также решить с использованием преобразования цепей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
16 В состав цепей постоянного тока входят: – E, J (источники напряжения и тока); – r (сопротивления). Элементы электрических цепей соединяются последовательно и параллельно. Законы Кирхгофа являются основой различных способов расчета электрических цепей. Многие частные задачи можно также решить с использованием преобразования цепей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
 Последовательность определения токов ветвей по законам Кирхгофа: 17 1. Выбираются направления токов ветвей. Число токов равно числу ветвей схемы. Токи ветвей с источниками токов известны. 2. Записываются уравнения по первому закону Кирхгофа. Их число на единицу меньше числа узлов схемы. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
Последовательность определения токов ветвей по законам Кирхгофа: 17 1. Выбираются направления токов ветвей. Число токов равно числу ветвей схемы. Токи ветвей с источниками токов известны. 2. Записываются уравнения по первому закону Кирхгофа. Их число на единицу меньше числа узлов схемы. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
 Последовательность определения токов ветвей по законам Кирхгофа: 18 (продолжение) 3. Выбираются независимые контуры и направления их обхода. 4. Записываются уравнения по второму закону Кирхгофа. При этом уравнения для контуров с источниками тока, не составляются! Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
Последовательность определения токов ветвей по законам Кирхгофа: 18 (продолжение) 3. Выбираются независимые контуры и направления их обхода. 4. Записываются уравнения по второму закону Кирхгофа. При этом уравнения для контуров с источниками тока, не составляются! Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 1. Тэттэр А. Ю. , Пономарев А. В.
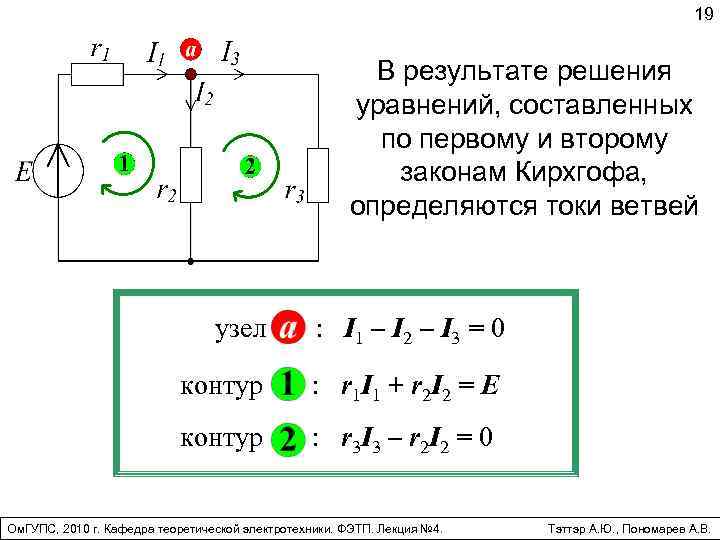 19 В результате решения уравнений, составленных по первому и второму законам Кирхгофа, определяются токи ветвей узел : I 1 – I 2 – I 3 = 0 контур : r 1 I 1 + r 2 I 2 = E контур : r 3 I 3 – r 2 I 2 = 0 Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
19 В результате решения уравнений, составленных по первому и второму законам Кирхгофа, определяются токи ветвей узел : I 1 – I 2 – I 3 = 0 контур : r 1 I 1 + r 2 I 2 = E контур : r 3 I 3 – r 2 I 2 = 0 Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
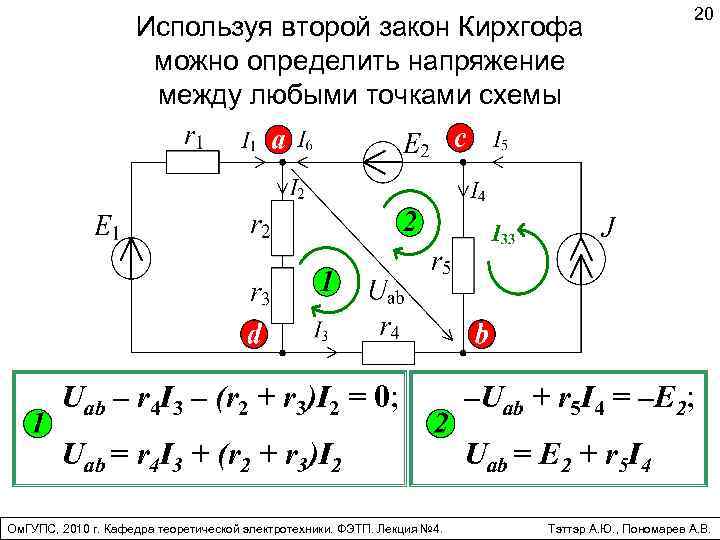 Используя второй закон Кирхгофа можно определить напряжение между любыми точками схемы 20 Uab – r 4 I 3 – (r 2 + r 3)I 2 = 0; –Uab + r 5 I 4 = –E 2; Uab = r 4 I 3 + (r 2 + r 3)I 2 Uab = E 2 + r 5 I 4 Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
Используя второй закон Кирхгофа можно определить напряжение между любыми точками схемы 20 Uab – r 4 I 3 – (r 2 + r 3)I 2 = 0; –Uab + r 5 I 4 = –E 2; Uab = r 4 I 3 + (r 2 + r 3)I 2 Uab = E 2 + r 5 I 4 Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 Последовательность определения токов ветвей методом контурных токов 21 1. Выбираются независимые контуры и направления контурных токов. 2. Записывается система уравнений в общем виде. Число уравнений равно числу независимых контуров схемы минус число контуров, содержащих источники тока. Количество слагаемых в левой части уравнения равно числу независимых контуров. ! Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 2. Тэттэр А. Ю. , Пономарев А. В.
Последовательность определения токов ветвей методом контурных токов 21 1. Выбираются независимые контуры и направления контурных токов. 2. Записывается система уравнений в общем виде. Число уравнений равно числу независимых контуров схемы минус число контуров, содержащих источники тока. Количество слагаемых в левой части уравнения равно числу независимых контуров. ! Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 2. Тэттэр А. Ю. , Пономарев А. В.
 Последовательность определения токов ветвей методом контурных токов 22 (продолжение) 3. Определяются коэффициенты при неизвестных – собственные и общие сопротивления контуров, а также контурные ЭДС. 4. Рассчитываются контурные токи. 5. Выбираются направления токов ветвей. 6. Определяются токи ветвей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 2. Тэттэр А. Ю. , Пономарев А. В.
Последовательность определения токов ветвей методом контурных токов 22 (продолжение) 3. Определяются коэффициенты при неизвестных – собственные и общие сопротивления контуров, а также контурные ЭДС. 4. Рассчитываются контурные токи. 5. Выбираются направления токов ветвей. 6. Определяются токи ветвей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 2. Тэттэр А. Ю. , Пономарев А. В.
 Пример использования МКТ Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. 23 Тэттэр А. Ю. , Пономарев А. В.
Пример использования МКТ Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. 23 Тэттэр А. Ю. , Пономарев А. В.
 24 Выбираем независимые контуры так, чтобы ветвь с источником тока не оказалась общей для контуров. Выбираем произвольно направления четырех контурных токов, причем один из них известен: I 44=J. В общем виде составляем систему уравнений относительно трех неизвестных контурных токов: r 11 I 11 + r 12 I 22 + r 13 I 33 + r 14 I 44 = E 11; r 21 I 11 + r 22 I 22 + r 23 I 33 + r 24 I 44 = E 22; r 31 I 11 + r 32 I 22 + r 33 I 33 + r 34 I 44 = E 33. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
24 Выбираем независимые контуры так, чтобы ветвь с источником тока не оказалась общей для контуров. Выбираем произвольно направления четырех контурных токов, причем один из них известен: I 44=J. В общем виде составляем систему уравнений относительно трех неизвестных контурных токов: r 11 I 11 + r 12 I 22 + r 13 I 33 + r 14 I 44 = E 11; r 21 I 11 + r 22 I 22 + r 23 I 33 + r 24 I 44 = E 22; r 31 I 11 + r 32 I 22 + r 33 I 33 + r 34 I 44 = E 33. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 25 r 11 I 11 + r 12 I 22 + r 13 I 33 + r 14 I 44 = E 11; r 21 I 11 + r 22 I 22 + r 23 I 33 + r 24 I 44 = E 22; r 31 I 11 + r 32 I 22 + r 33 I 33 + r 34 I 44 = E 33. r 11= r 1+r 2; r 22= r 4+r 5+r 6; r 33= r 1+r 3+r 4; r 12= r 21= 0; r 14= 0; r 24= – r 4; r 13= r 31= –r 1; r 23= r 32= –r 4; r 34= r 3+r 4; E 11= E 2; E 22= E 3; E 33= –E 1; Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
25 r 11 I 11 + r 12 I 22 + r 13 I 33 + r 14 I 44 = E 11; r 21 I 11 + r 22 I 22 + r 23 I 33 + r 24 I 44 = E 22; r 31 I 11 + r 32 I 22 + r 33 I 33 + r 34 I 44 = E 33. r 11= r 1+r 2; r 22= r 4+r 5+r 6; r 33= r 1+r 3+r 4; r 12= r 21= 0; r 14= 0; r 24= – r 4; r 13= r 31= –r 1; r 23= r 32= –r 4; r 34= r 3+r 4; E 11= E 2; E 22= E 3; E 33= –E 1; Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 26 Выбрав направления токов ветвей, получим: I 1= –I 33; I 5= I 22; I 2= I 11; I 6= I 11 – I 33; I 3= I 33 + I 44; I 7= I 44=J. I 4= I 33 + I 44 – I 22; Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
26 Выбрав направления токов ветвей, получим: I 1= –I 33; I 5= I 22; I 2= I 11; I 6= I 11 – I 33; I 3= I 33 + I 44; I 7= I 44=J. I 4= I 33 + I 44 – I 22; Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 Последовательность определения токов ветвей методом узловых потенциалов: 27 1. Записывается система уравнений в общем виде. Число уравнений системы на единицу меньше числа узлов схемы. ! Если в схеме содержится ветвь с источником ЭДС без сопротивлений, то φ2 = φ1 + Е. Приняв φ1, равным 0, получим φ2=Е. Уравнение для φ2 – убирается! Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 2. Тэттэр А. Ю. , Пономарев А. В.
Последовательность определения токов ветвей методом узловых потенциалов: 27 1. Записывается система уравнений в общем виде. Число уравнений системы на единицу меньше числа узлов схемы. ! Если в схеме содержится ветвь с источником ЭДС без сопротивлений, то φ2 = φ1 + Е. Приняв φ1, равным 0, получим φ2=Е. Уравнение для φ2 – убирается! Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 2. Тэттэр А. Ю. , Пономарев А. В.
 Последовательность определения токов ветвей методом узловых потенциалов: 28 (продолжение) 2. Определяются коэффициенты при неизвестных – собственные и общие проводимости, а также задающие токи узлов. 3. Рассчитываются потенциалы узлов. 4. Выбираются направления токов ветвей. 5. Определяются токи ветвей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 2. Тэттэр А. Ю. , Пономарев А. В.
Последовательность определения токов ветвей методом узловых потенциалов: 28 (продолжение) 2. Определяются коэффициенты при неизвестных – собственные и общие проводимости, а также задающие токи узлов. 3. Рассчитываются потенциалы узлов. 4. Выбираются направления токов ветвей. 5. Определяются токи ветвей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 2. Тэттэр А. Ю. , Пономарев А. В.
 Пример использования МУП Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. 29 Тэттэр А. Ю. , Пономарев А. В.
Пример использования МУП Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. 29 Тэттэр А. Ю. , Пономарев А. В.
 30 В схеме 2 узла и 4 ветви или: I 4 = I 1 + I 2 + I 3. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
30 В схеме 2 узла и 4 ветви или: I 4 = I 1 + I 2 + I 3. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
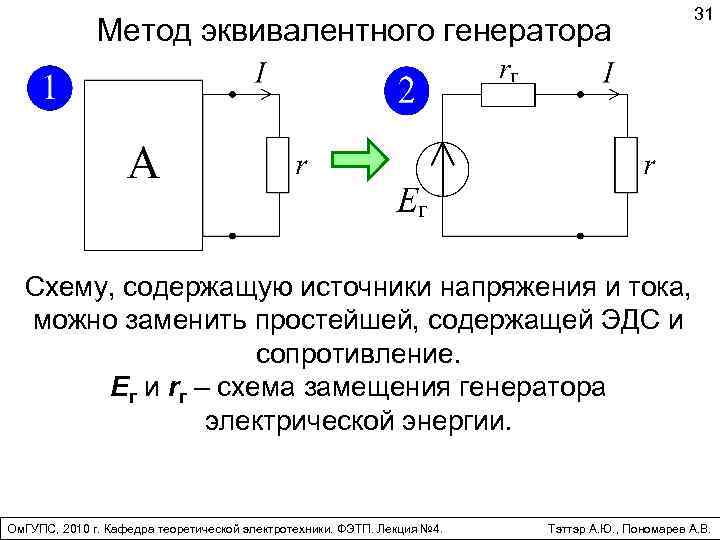 Метод эквивалентного генератора 31 Схему, содержащую источники напряжения и тока, можно заменить простейшей, содержащей ЭДС и сопротивление. Eг и rг – схема замещения генератора электрической энергии. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
Метод эквивалентного генератора 31 Схему, содержащую источники напряжения и тока, можно заменить простейшей, содержащей ЭДС и сопротивление. Eг и rг – схема замещения генератора электрической энергии. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 32 rг – входное сопротивление схемы относительно зажимов выделенной ветви. Источники E и J заменяются их внутренними сопротивлениями. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
32 rг – входное сопротивление схемы относительно зажимов выделенной ветви. Источники E и J заменяются их внутренними сопротивлениями. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 33 Баланс мощностей На основании закона сохранения энергии мощность, потребляемая в электрической цепи, должна быть равна мощности, поставляемой источниками. В состав потребляемой мощности входит мощность, рассеиваемая в сопротивлениях, а также мощность источников, находящихся в режиме потребителей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
33 Баланс мощностей На основании закона сохранения энергии мощность, потребляемая в электрической цепи, должна быть равна мощности, поставляемой источниками. В состав потребляемой мощности входит мощность, рассеиваемая в сопротивлениях, а также мощность источников, находящихся в режиме потребителей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
 Уравнение баланса мощностей имеет вид: 34 или Примеры для определения знаков слагаемых приведены на рисунках а, б, в. a б Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. в Тэттэр А. Ю. , Пономарев А. В.
Уравнение баланса мощностей имеет вид: 34 или Примеры для определения знаков слагаемых приведены на рисунках а, б, в. a б Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. в Тэттэр А. Ю. , Пономарев А. В.
 Пример 35 Uab = Jrab; I 1 = Uab / r 1; I 1 = 1/1 = 1 А; I 2 = Uab / r 2; J = 2 А; r 1 = 1 Ом; r 2 = 1 Ом. Uab = 2· 0, 5 = 1 В; I 2 = 1/1 = 1 А; Pист = JUab; Pист = 2· 1 = 2 Вт; Pпотр = r 1 I 12 + r 2 I 22; Pпотр = 1· 12 + 1· 12 = 2 Вт; Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.
Пример 35 Uab = Jrab; I 1 = Uab / r 1; I 1 = 1/1 = 1 А; I 2 = Uab / r 2; J = 2 А; r 1 = 1 Ом; r 2 = 1 Ом. Uab = 2· 0, 5 = 1 В; I 2 = 1/1 = 1 А; Pист = JUab; Pист = 2· 1 = 2 Вт; Pпотр = r 1 I 12 + r 2 I 22; Pпотр = 1· 12 + 1· 12 = 2 Вт; Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция № 4. Тэттэр А. Ю. , Пономарев А. В.


