Лекция № 4 -5 Тема: Основные понятия дискретной

Лекция № 4 -5 Лекция № 4 -5 Тема: Основные понятия дискретной математики. Элементы теории вероятностей.

Общая цель модуля : изучить основные понятия дискретной математики и теории вероятностей и применять их при решении задач. Конкретные цели. Студент должен знать : — элементы математической логики; — определение факториала; — основные понятия комбинаторики: перестановки, размещения, сочетания; — понятие случайного события, частоты события, вероятности события. Студент должен уметь : — производить операции дизъюнкции, конъюнкции, отрицания; — различать комбинации, состоящие из заданных объектов, подчиненные тем или иным условиям; — находить число перестановок, размещений и сочетаний, пользуясь соответствующими формулами; — определять вероятность события, применяя основные теоремы и формулы.

ПЛАН. 1. Понятие множества. Способы задания множеств. 2. Операции над множествами. 3. Элементы математической логики. 4. Основные понятия комбинаторики. 5. Определение вероятности события. 6. Основные теоремы и формулы теории вероятностей. ЛИТЕРАТУРА: 1. С. Г. Григорьев. Математика. Гл. 5. п. 5. 1. 1, 5. 1. 2, 5. 1. 3. Стр. 213 -216. И. Д. Пехлецкий. Математика. Гл. 1. п. 1. 1. Стр. 11 -14. 2. С. Г. Григорьев. Математика. Гл. 5. п. 5. 1. 1, 5. 1. 2, 5. 1. 3. Стр. 213 -216. И. Д. Пехлецкий. Математика. Гл. 1. п. 1. 1. Стр. 11 -14. 3. С. Г. Григорьев. Математика. Гл. 5. п. 5. 2. Стр. 222 -226. 4. С. Г. Григорьев. Математика. Гл. 7. п. 7. 2. Стр. 2264 -266. И. Д. Пехлецкий. Математика. Гл. 10. п. 10. 2. Стр. 208 -210. 5. С. Г. Григорьев. Математика. Гл. 7. п. 7. 1. Стр. 259 -262. И. Д. Пехлецкий. Математика. Гл. 10. . Стр. 200 -204. 6. С. Г. Григорьев. Математика. Гл. 7. п. 7. 3. Стр. 267 -272, п. 7. 4. Стр. 274 -278, п. 7. 5. Стр. 282, 283. И. Д. Пехлецкий. Математика. Гл. 10. п. 10. 2. 2. Стр. 210 -214, п. 10. 2. 3.

1. ПОНЯТИЕ МНОЖЕСТВА. СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ. определяемые через первичные понятия первичные или уже известные ВСЕ ПОНЯТИЯ МАТЕМАТИКИ МНОЖЕСТВО

3. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ. Исходное понятие – понятие высказывания. Определение : Высказыванием называется предложение, которое может быть либо истинным, либо ложным. Примеры : снег — белый – истинное высказывание; Волга впадает в Средиземное море – ложное высказывание 2+2=10 – ложное высказывание; Вопросительные , восклицательные предложения, предложения которые служат определениями не являются высказываниями. Примеры: «Который час? » ; «Мойте руки перед едой!» ; «Трапецией называется четырехугольник, две стороны которого параллельны»

ОПЕРАЦИЯ ОТРИЦАНИЯ. Определение. Отрицанием высказывания Р называется новое высказывание, обозначаемое (читается «не Р» , или «неверно, что Р» ), которое считается истинным, если высказывание Р ложно, и ложным, если Р истинно. Примеры : 2 N (истинно), 2 N (ложно) 2 3 (ложно) 2+3 =5 (истинно), 2+3 5 (ложно) Введем некоторую функцию α (Ρ) = Таблица истинности для отрицания ложно. Риевысказыванесли истинно. Риевысказыванесли , 0 , 1 α ( ) 1 0 0 1 РР Р

КОНЪЮНКЦИЯ ВЫСКАЗЫВАНИЙ. Определение. Конъюнкцией высказываний Р и Q называется новое высказывание, обозначаемое Р ^ Q (читается «Р и Q » ), которое считается истинным, если истинны оба высказывания Р и Q , и ложным во всех остальных случаях. Таблица истинности конъюнкции высказываний Примеры : 1) «Число 2 простое и четное» — конъюнкция высказываний «Число 2 простое» и «Число 2 четное» . 2) « 2 меньше 5» и « 5 меньше 10» — конъюнкцией этих высказываний будет высказывание « 2 меньше 5 и 5 меньше 10» 2<5<10 α (Ρ) α ( Q ) α (Р ^ Q )

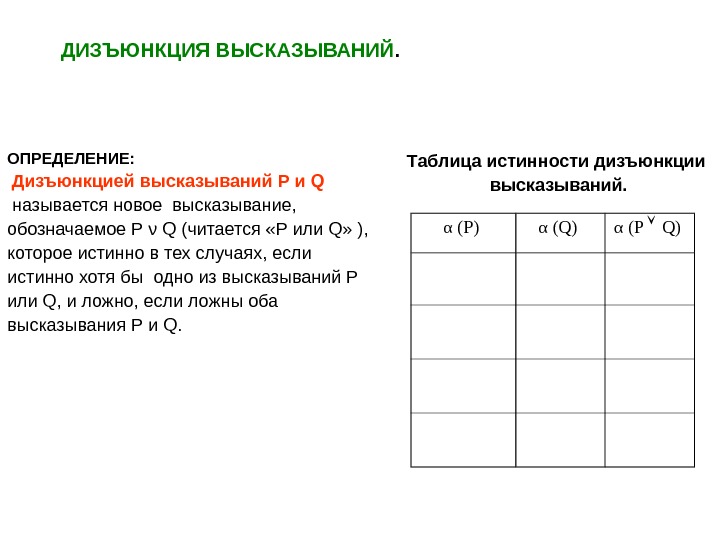
ДИЗЪЮНКЦИЯ ВЫСКАЗЫВАНИЙ. ОПРЕДЕЛЕНИЕ: Дизъюнкцией высказываний Р и Q называется новое высказывание, обозначаемое Р ν Q (читается «Р или Q » ), которое истинно в тех случаях, если истинно хотя бы одно из высказываний Р или Q , и ложно, если ложны оба высказывания Р и Q. α (Ρ) α ( Q ) α (Р Q ) Таблица истинности дизъюнкции высказываний.

ФАКТОРИАЛ. Определение. 1 · 2 · 3 ·…· n = n ! Вычислим: 1!=1 6!=5! · 6=720 2!= 2 · 1=2 7!=5040 3!=3 · 2 · 1=6 8!=40320 4!=3! · 4=24 9!=362880 5!=4! · 5=24 · 5=120 10!=3628800 ( n +1)! = n ! ( n +1) n =0 1! = 0! · 1 Запомнить 0!=

СОЕДИНЕНИЯ. Пусть Х – множество, состоящее из n элементов. Х= { x 1 , х 2 , …, х n }. Элементами множества Х могут быть различные объекты, объединенные каким-нибудь общим признаком или свойством. Например. Множество студентов, множество четных чисел, множество букв латинского алфавита и т. д. Из элементов множества Х будем образовывать различные подмножества, содержащие m элементов (1 ≤ m ≤ n)¸ которые называются соединениями. Поставленную задачу можно сформулировать так: «Сколько существует подмножеств из n элементов множества Х по m ? » . Различают 3 вида соединений.

Определение 1. Размещениями из n элементов по m называются соединения, содержащие каждое m элементов из данных n элементов множества Х, которые отличаются друг от друга либо самими элементами, либо их порядком. Обозначение = n ( n -1) ( n -2)…( n — m +1) 1 ≤ m ≤ n Пример. Сколькими способами можно составить расписание одного учебного дня, если изучается 6 учебных дисциплин и читается 4 лекции в день. = 6 · 5 · 4 · 3= 360 Задание на дом. Посчитать для своего учебного заведения. Можно сделать в виде таблицы. m n. А

Определение 2. Перестановками из данных n элементов множества Х по n называются соединения, каждое из которых содержит n элементов, и которые отличаются друг от друга только порядком элементов. Обозначение Р n = = n · ( n -1) · . . . · 2 · 1= n! Р n = n! Пример. Сколькими способами можно составить программу выступления из 9 номеров. Р 9 = 9! = 1· 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 = 362 880 n n.

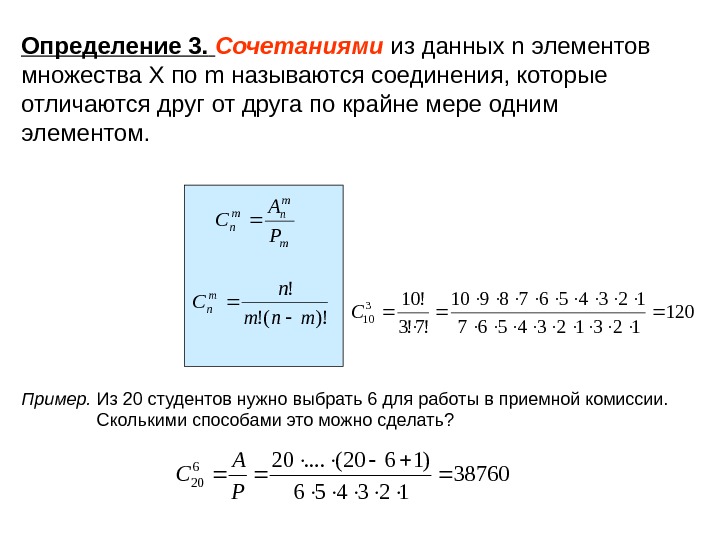
Определение 3. Сочетаниями из данных n элементов множества Х по m называются соединения, которые отличаются друг от друга по крайне мере одним элементом. Пример. Из 20 студентов нужно выбрать 6 для работы в приемной комиссии. Сколькими способами это можно сделать? 120 12312345678910 !7!3 !10 3 10 Сm m nm n P A C )!(! ! mnm n Cm n 38760 123456 )1620(. . 206 20 P A С

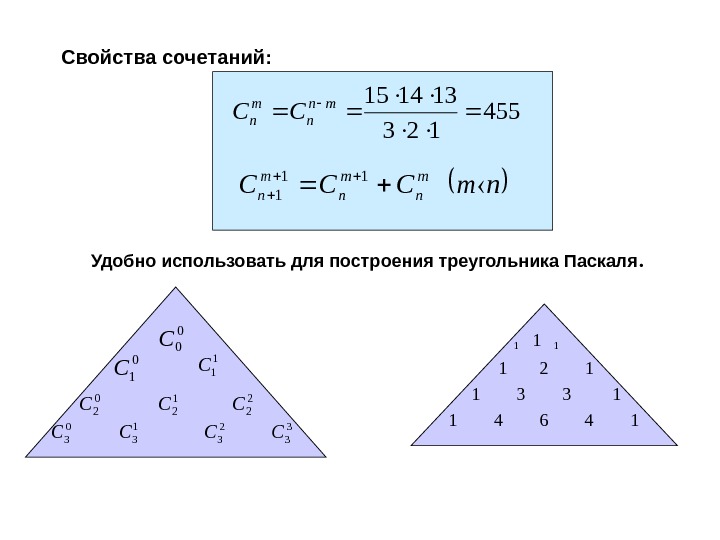
Свойства сочетаний: Удобно использовать для построения треугольника Паскаля. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 455 123 131415 mn n m n. CC nm. CCС m n m n 11 1 0 0 C 0 1 C 1 1 C 0 2 C 1 2 C 2 2 C 0 3 C 1 3 C 2 3 С 3 3 С

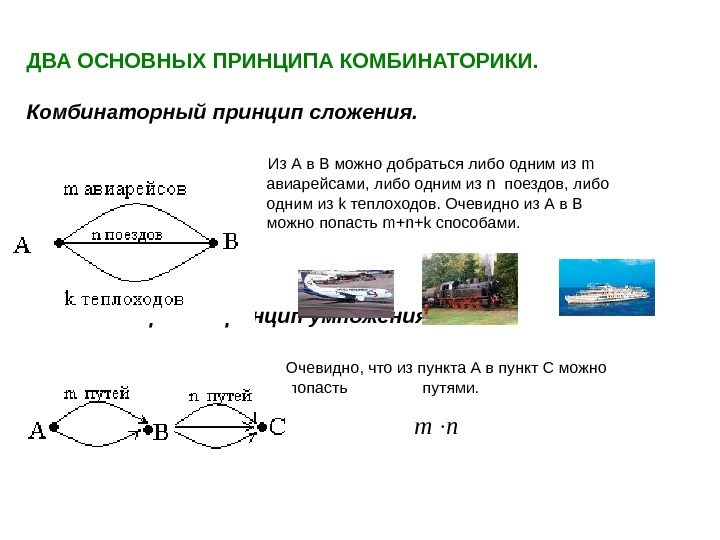
ДВА ОСНОВНЫХ ПРИНЦИПА КОМБИНАТОРИКИ. Комбинаторный принцип сложения. Из А в В можно добраться либо одним из m авиарейсами, либо одним из n поездов, либо одним из k теплоходов. Очевидно из А в В можно попасть m + n + k способами. Комбинаторный принцип умножения. Очевидно, что из пункта А в пункт С можно попасть путями. nm

ПОНЯТИЕ О СЛУЧАЙНОМ СОБЫТИИ. Опыт, эксперимент, наблюдение явления называются испытанием. Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика). Результат (исход) испытания называется событием. Событиями являются: выпадение герба или выпадение цифры, попадание в цель или промах, появление того или иного числа очков на брошенной игральной кости.

Определение. Два события называются совместными , если появление одного из них не исключает появления другого в одном и том же испытании. Пример. Испытание: однократное бросание игральной кости. Событие А- появление трех очков, событие В- появление нечетного числа очков. Событие А и В совместные. Определение. Два события называются несовместными , если появление одного из них исключает появление другого в одном и том же испытании. Пример. Испытание: однократное бросание монеты. Событие А – выпадение «герба» , событие В – выпадение цифры. Эти события несовместные, так как появление одного из них исключает появление другого. Или, например, при одном бросании кости появление не менее трех очков и появление четной грани – события совместные, а появление цифры 3 и при этом появление четной грани — события несовместные

Определение. Два события А и В называются противоположными , если в данном испытании они несовместны и одно из них обязательно происходит. Событие, противоположное событию А, обозначают Пример. Испытание: бросание монеты. Событие А – выпадение «герба» , событие В – выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они и появление одного из них исключает появление другого, т. е. Определение. Событие называется достоверным , если в данном испытании оно является единственно возможным исходом, и невозможным , если в данном испытании оно заведомо не может произойти. Пример. Испытание: извлечение шара из урны, в которой все шары желтые. Событие А – вынут желтый шар – достоверное событие; событие В – вынут черный шар – невозможное событие. А ВАили. ВА

Определение. Событие А называется случайным , если оно объективно может наступить или не наступить в данном испытании. Пример. Событие — выпадение четырех очков при бросании игральной кости – случайное. Оно может наступить, но оно может и не наступить в данный момент испытании. ЧАСТОТА И ВЕРОЯТНОСТЬ СОБЫТИЯ. Пусть А- случайное событие, связанное с некоторым опытом. Повторим опыт n раз в одних и тех же условиях и пусть при этом событие А появилось m раз. Определение. Отношение числа m опытов, в которых событие А появилось, к общему числу n проведенных опытов называется частотой события А. Оказывается, что при многократном повторении опыта частота события принимает значения, близкие к некоторому постоянному числу р. Свойство устойчивости частоты случайного события было подмечено на явлениях демографического характера. Подсчитано, например, что частота рождения мальчика колеблется около числа 0, 517. 4 А n m

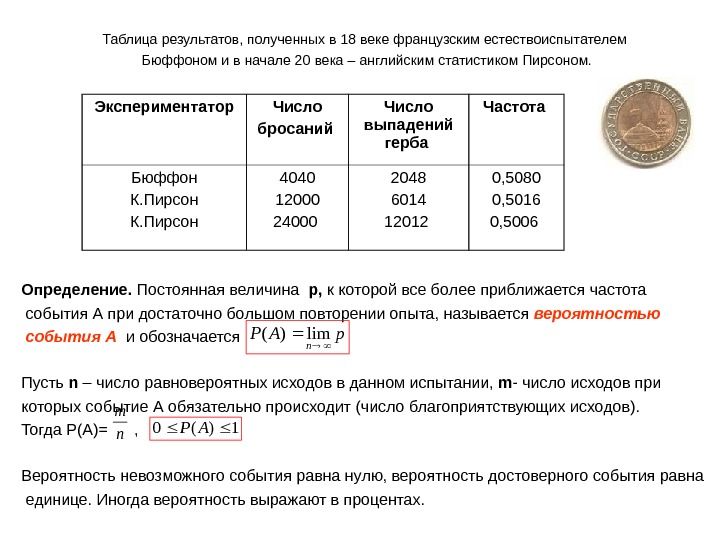
Таблица результатов, полученных в 18 веке французским естествоиспытателем Бюффоном и в начале 20 века – английским статистиком Пирсоном. Определение. Постоянная величина р, к которой все более приближается частота события А при достаточно большом повторении опыта, называется вероятностью события А и обозначается Пусть n – число равновероятных исходов в данном испытании, m — число исходов при которых событие А обязательно происходит (число благоприятствующих исходов). Тогда Р(А)= , Вероятность невозможного события равна нулю, вероятность достоверного события равна единице. Иногда вероятность выражают в процентах. Экспериментатор Число бросаний Число выпадений герба Частота Бюффон К. Пирсон 4040 12000 24000 2048 6014 12012 0, 5080 0, 5016 0, 5006 p. AP n lim)( n m 1)(0 AP

Определение. Суммой А+В двух событий А и В называется событие, состоящее в появлении либо события А, либо события В, либо обоих этих событий вместе. Определение. Произведением событий А и В называется событие С=АВ, состоящее в том, что в результате испытания произошли и событие А, и событие В. Пример. Испытание: стрельба двух стрелков (каждый делает по выстрелу). Событие А — попадание в мишень первым стрелком, В – попадание в мишень вторым стрелком. Суммой событий А и В будет событие С=А+В, состоящее в попадании в мишень по крайней мере одним стрелком. Произведением событий А и В будет событие D = AB , состоящее в попадании в мишень двух стрелков. Условная вероятность – вероятность появления события А при условии, что произошло событие В, обозначается . События А и В называются независимыми , если условная вероятность Р В А равна вероятности Р(А). AP

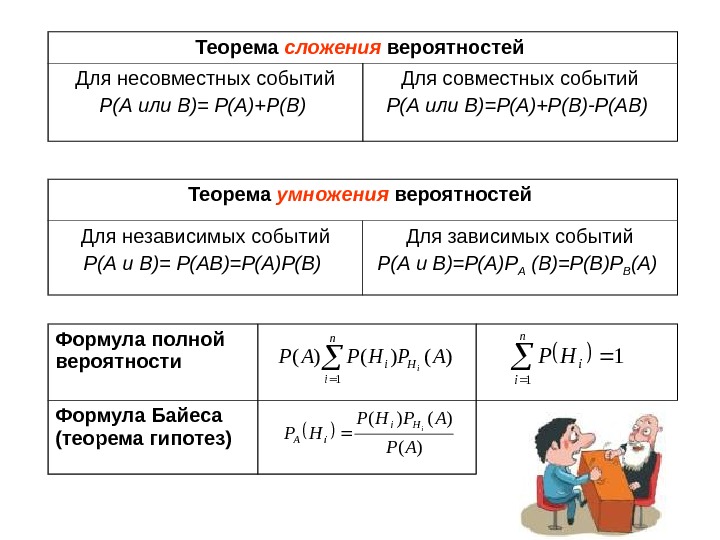
Теорема сложения вероятностей Для несовместных событий Р(А или В)= Р(А)+Р(В) Для совместных событий Р(А или В)=Р(А)+Р(В)-Р(АВ) Теорема умножения вероятностей Для независимых событий Р(А и В)= Р(АВ)=Р(А)Р(В) Для зависимых событий Р(А и В)=Р(А)Р А (В)=Р(В)Р В (А) Формула полной вероятности Формула Байеса (теорема гипотез) )()()( 1 APHPAPi. H n i i 1 1 n i i. HP )( )()( AP APHP HPi. Hi i.

Случайное событие является в первую очередь качественной характеристикой опыта. Однако, при рассмотрении результатов опыта часто помимо самого факта наступления или ненаступления исследуемого события интересуются некоторыми количественными характеристиками. Определение. Величина, которая в результате опыта может принимать одно и только одно определенное значение, до опыта неизвестное и зависящее от причин, которые нельзя учесть заранее, называется случайной величиной. Названия случайной величины обычно обозначают заглавными буквами: а их возможные значения – прописными буквами: , . . . , , , ZYX, . . , , zyx

Случайные величины дискретные непрерывные

Всякое соотношени е, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями называется законом распределения этой случайной величины. Пример 1 : Пусть случайная величина Х — число очков, выпавших при подбрасывании игральной кости. Найти закон распределения. Пример 2 : Рассматривается случайная величина Х – число появлений события А в серии из n независимых опытов, в каждом из которых А наступает с вероятностью p. Найти распределение случайной величины Х. Случайная величина Х может, очевидно, принимать одно из следующих значений: Вероятность события, состоящего в том, что случайная величина Х примет значение, равное k , определяется формулой Я. Бернулли: , где . Следовательно, распределение случайной величины Х может быть написано так: Распределение, описываемое таблицей, называется распределением Я. Бернулли или биномиальным распределением. 1 2 3 4 5 6. , . . . , 2, 1, 0 nk knkk nqp. Ck. XP)(pq 1 0 1 … k … n ix ip 6 1 6 1 6 1 n n qp. C 00 111 n n qp. C knkk nqp. C 0 qp. Cnn n

Пример 3. Если среднее время безотказной работы компьютера данного типа равно s часов, то вероятность проработать без отказа не менее t часов может быть выражена законом распределения в форме , t ≥ 0. stet. TP)(

Основные характеристики случайных величин Определение. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений на их вероятности : Разность между случайной величиной Х и ее математическим ожиданием М(Х), т. е. Х-М(Х) называется отклонением. Определение. Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата ее отклонения: Удобной для вычисления дисперсий является формула: Для примера 1: М(Х)= M ( X 2 )= D ( X )=15, 2 — (3, 5)² =2, 95 Для примера 2: М(Х)= np , D ( X )= npq , где q =1 — p. ip n i iinnpxpx. XM 1 2211. . . )( 2))(()(XMXMXD 22))(()()(XMXMXD 5, 3 6 2121 6 1)654321( 6 16 6 15 6 14 6 13 6 12 6 11 6 1 2, 15)362516941(