l4_2012_09_19.ppt
- Количество слайдов: 32
 Лекция 4 (19. 09. 2012) 1. Физические тензоры и преобразования координат 2. Тензор проводимости и закон Ома 3. Преобразование координат группы Oh 4. Элементы континуальной теории упругости Литература: 1. У. Харрисон, "Теория твердого тела", Глава I. 2. А. Келли, Г. Гровс, “Кристаллография и дефекты в кристаллах”. 3. Ландау и Лифшиц, том VII "Теория упругости", Глава I (П 1, 2, 5).
Лекция 4 (19. 09. 2012) 1. Физические тензоры и преобразования координат 2. Тензор проводимости и закон Ома 3. Преобразование координат группы Oh 4. Элементы континуальной теории упругости Литература: 1. У. Харрисон, "Теория твердого тела", Глава I. 2. А. Келли, Г. Гровс, “Кристаллография и дефекты в кристаллах”. 3. Ландау и Лифшиц, том VII "Теория упругости", Глава I (П 1, 2, 5).
 Физические тензоры и преобразования координат Тензор: 1. целостный математический объект; 2. получает численные компоненты при выборе системы координат (СК); 3. при изменении системы координат компоненты тензора преобразуются по общему тензорному закону. Тензор описывает некоторое свойство физического объекта, обычно настолько сложное, что требует нескольких числовых характеристик. Однако тензор не является матрицей, то есть простой совокупностью чисел. Тензор – целостный математический объект, компоненты которого подчиняются “закону сохранения тензора”. Назвав матрицу тензором, мы приписываем ей правило преобразования при смене СК. Точнее, не само правило, которое общее для всех тензоров, а способность сохранять физический смысл при таком преобразовании в “новой” СК. Это – важнейшее свойство всех тензоров.
Физические тензоры и преобразования координат Тензор: 1. целостный математический объект; 2. получает численные компоненты при выборе системы координат (СК); 3. при изменении системы координат компоненты тензора преобразуются по общему тензорному закону. Тензор описывает некоторое свойство физического объекта, обычно настолько сложное, что требует нескольких числовых характеристик. Однако тензор не является матрицей, то есть простой совокупностью чисел. Тензор – целостный математический объект, компоненты которого подчиняются “закону сохранения тензора”. Назвав матрицу тензором, мы приписываем ей правило преобразования при смене СК. Точнее, не само правило, которое общее для всех тензоров, а способность сохранять физический смысл при таком преобразовании в “новой” СК. Это – важнейшее свойство всех тензоров.
 Компоненты тензора получают численные значения только тогда, когда выбрана система координат. Однако систем координат может быть введено множество, а физическая величина, описываемая тензором – одна на всех. Если компоненты тензора вычислены в одной СК, то как определить их аналоги в другой? Тензорное исчисление дает на это изящный ответ: все компоненты тензора преобразуются по общему тензорному правилу, независимо от их физического смысла. Закон преобразования тензоров вытекает из закона преобразования системы координат. Как задать этот закон? Пусть имеется ортогональная СК, заданная тройкой базисных векторов (е 1, е 2, е 3). Можно выразить каждый базисный вектор новой СК (е 1', е 2', е 3') через базисные векторы старой СК как их линейную комбинацию:
Компоненты тензора получают численные значения только тогда, когда выбрана система координат. Однако систем координат может быть введено множество, а физическая величина, описываемая тензором – одна на всех. Если компоненты тензора вычислены в одной СК, то как определить их аналоги в другой? Тензорное исчисление дает на это изящный ответ: все компоненты тензора преобразуются по общему тензорному правилу, независимо от их физического смысла. Закон преобразования тензоров вытекает из закона преобразования системы координат. Как задать этот закон? Пусть имеется ортогональная СК, заданная тройкой базисных векторов (е 1, е 2, е 3). Можно выразить каждый базисный вектор новой СК (е 1', е 2', е 3') через базисные векторы старой СК как их линейную комбинацию:
 Из коэффициентов преобразования можно составить матрицу преобразования Тогда в более компактной форме или . Пример: или Двумерный случай вращения системы координат на угол α. α Матрица этого преобразования:
Из коэффициентов преобразования можно составить матрицу преобразования Тогда в более компактной форме или . Пример: или Двумерный случай вращения системы координат на угол α. α Матрица этого преобразования:
 Любой тензор характеризуется рангом (сложностью, информативностью) и мерностью (количеством измерений пространства, степенью свободы). Ранг тензора непосредственно связан с его смысловым содержанием, а мерность является следствием количества измерений СК (число базисных векторов). Число компонент тензора равно его мерности, возведенной в степень, равную его рангу. Скаляр (тензор 0 -го ранга) – величина, которая не меняется при преобразованиях системы координат (масса, заряд, электростатический потенциал и т. д. ) Преобразование компонент вектора при смене СК: Компоненты вектора x преобразуются так же, как векторы базиса ei.
Любой тензор характеризуется рангом (сложностью, информативностью) и мерностью (количеством измерений пространства, степенью свободы). Ранг тензора непосредственно связан с его смысловым содержанием, а мерность является следствием количества измерений СК (число базисных векторов). Число компонент тензора равно его мерности, возведенной в степень, равную его рангу. Скаляр (тензор 0 -го ранга) – величина, которая не меняется при преобразованиях системы координат (масса, заряд, электростатический потенциал и т. д. ) Преобразование компонент вектора при смене СК: Компоненты вектора x преобразуются так же, как векторы базиса ei.
 Вектор (тензор 1 -го ранга, размерность 3) – величина, определяемая в каждой системе координат тремя числами, причем при переходе от одной системы координат к другой компоненты вектора преобразуются как координаты точки. Тензор n-го ранга (размерность 3) – физическая величина, характеризуемая элементами (i 1, . . , in = 1, 2, 3), которые при преобразовании координат П преобразуются по закону: Говорят, что компоненты тензора преобразуются как произведения индексов.
Вектор (тензор 1 -го ранга, размерность 3) – величина, определяемая в каждой системе координат тремя числами, причем при переходе от одной системы координат к другой компоненты вектора преобразуются как координаты точки. Тензор n-го ранга (размерность 3) – физическая величина, характеризуемая элементами (i 1, . . , in = 1, 2, 3), которые при преобразовании координат П преобразуются по закону: Говорят, что компоненты тензора преобразуются как произведения индексов.
 Такое определение оправдано общим видом большинства физических законов: где А – воздействие, D – свойство, независящее от воздействия, В – отклик. В линейном приближении общий вид такой связи выглядит так При изменении системы координат эта зависимость записывается в виде: Можно показать: Для того, чтобы две формулы описывали одну и ту же зависимость отклика от воздействия, необходимо и достаточно, чтобы свойство D преобразовывалось бы при преобразовании координат как компоненты тензора.
Такое определение оправдано общим видом большинства физических законов: где А – воздействие, D – свойство, независящее от воздействия, В – отклик. В линейном приближении общий вид такой связи выглядит так При изменении системы координат эта зависимость записывается в виде: Можно показать: Для того, чтобы две формулы описывали одну и ту же зависимость отклика от воздействия, необходимо и достаточно, чтобы свойство D преобразовывалось бы при преобразовании координат как компоненты тензора.
 Физические тензоры и симметрия направлений в кристаллах Любому точечному преобразованию в кристалле соответствует матрица, описывающая преобразование координат Примеры: - Инверсия относительно нуля (i): (x, y, z) --> (-x, -y, -z) - Отражение в плоскости, проходящей через начало координат перпендикулярно оси x (σx): (x, y, z) --> (-x, y, z) – Поворот C 4 вокруг оси z: (x, y, z)→ (y, –x, z)
Физические тензоры и симметрия направлений в кристаллах Любому точечному преобразованию в кристалле соответствует матрица, описывающая преобразование координат Примеры: - Инверсия относительно нуля (i): (x, y, z) --> (-x, -y, -z) - Отражение в плоскости, проходящей через начало координат перпендикулярно оси x (σx): (x, y, z) --> (-x, y, z) – Поворот C 4 вокруг оси z: (x, y, z)→ (y, –x, z)
 Совершим последовательно два точечных преобразования, описываемых матрицами преобразования координат Π 1 и Π 2. Произвольная точка с координатами r в результате этих преобразований будет иметь координаты r ': Произведению преобразований симметрии соответствует произведение матриц преобразования координат. Другими словами преобразования симметрии и соответствующие им матрицы перемножаются по одной и той же таблице умножения: Группа преобразований точечной симметрии изоморфна группе соответствующих матриц преобразования координат. Группа матриц преобразования координат является представлением группы преобразований симметрии Симметрия направлений кристалла (кристаллический класс) определяет структуру тензоров, описывающих их свойства.
Совершим последовательно два точечных преобразования, описываемых матрицами преобразования координат Π 1 и Π 2. Произвольная точка с координатами r в результате этих преобразований будет иметь координаты r ': Произведению преобразований симметрии соответствует произведение матриц преобразования координат. Другими словами преобразования симметрии и соответствующие им матрицы перемножаются по одной и той же таблице умножения: Группа преобразований точечной симметрии изоморфна группе соответствующих матриц преобразования координат. Группа матриц преобразования координат является представлением группы преобразований симметрии Симметрия направлений кристалла (кристаллический класс) определяет структуру тензоров, описывающих их свойства.
 Пример: тензор проводимости и закон Ома Зависимость плотности тока в кристалле от приложенного электрического поля в линейном приближении в определенной системе координат будет иметь вид: или еще короче: В тензорных выражениях суммирование по 3 -м координатам подразумевается по всем совпадающим значкам. σik - тензор второго ранга, описывающий “свойство” кристалла – проводимость.
Пример: тензор проводимости и закон Ома Зависимость плотности тока в кристалле от приложенного электрического поля в линейном приближении в определенной системе координат будет иметь вид: или еще короче: В тензорных выражениях суммирование по 3 -м координатам подразумевается по всем совпадающим значкам. σik - тензор второго ранга, описывающий “свойство” кристалла – проводимость.
 В новой системе координат: Согласно общему правилу, компоненты тензора для двух систем координат связаны как I’ k’ Вспомним Для тензора первого ранга (вектора) закон преобразования тензора совпадает с законом преобразования координат точки : Для тензора второго ранга закон преобразования тензора совпадает с законом преобразования произведения координат Так же как и (доказательство –обязательная домашняя задача) Аналогичное правило перемножения значков работает для тензоров произвольного ранга
В новой системе координат: Согласно общему правилу, компоненты тензора для двух систем координат связаны как I’ k’ Вспомним Для тензора первого ранга (вектора) закон преобразования тензора совпадает с законом преобразования координат точки : Для тензора второго ранга закон преобразования тензора совпадает с законом преобразования произведения координат Так же как и (доказательство –обязательная домашняя задача) Аналогичное правило перемножения значков работает для тензоров произвольного ранга
 Рассмотрим преобразование компонент тензора при простых точечных преобразованиях, приводящих к перестановке индексов и смене их знаков - Отражение в плоскости, проходящей через начало координат перпендикулярно оси x (σx): (x, y, z) --> (-x, y, z) правило преобразования тензора: Работает правило перемножения значков! Итак, если известен закон преобразования координат, соответствующий некоторой операции симметрии кристалла, правило перемножения значков позволяет легко определить закон преобразования компонент тензора
Рассмотрим преобразование компонент тензора при простых точечных преобразованиях, приводящих к перестановке индексов и смене их знаков - Отражение в плоскости, проходящей через начало координат перпендикулярно оси x (σx): (x, y, z) --> (-x, y, z) правило преобразования тензора: Работает правило перемножения значков! Итак, если известен закон преобразования координат, соответствующий некоторой операции симметрии кристалла, правило перемножения значков позволяет легко определить закон преобразования компонент тензора
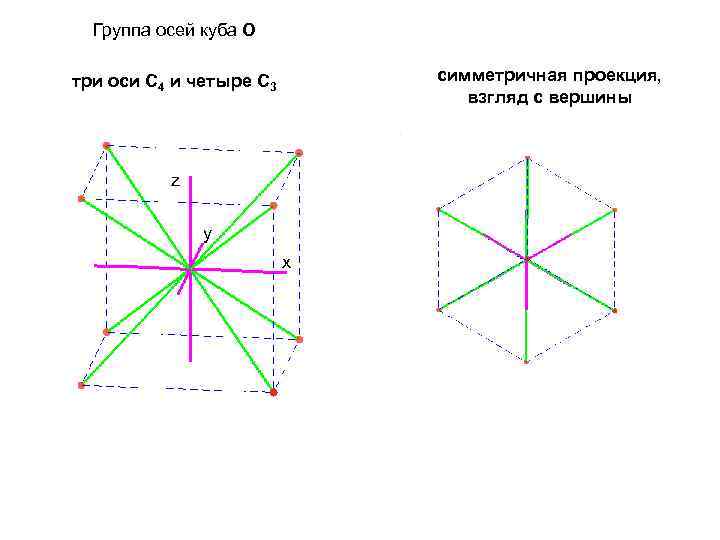 Группа осей куба О симметричная проекция, взгляд с вершины три оси C 4 и четыре С 3 z y x
Группа осей куба О симметричная проекция, взгляд с вершины три оси C 4 и четыре С 3 z y x
 - Инверсия (i): (x, y, z) ->(-x, -y, -z) Симметрия кристалла накладывает ограничение на вид любого тензора, описывающего свойства: если преобразованиях симметрии направлений направления в кристалле переходят в эквивалентные, то и тензор, характеризующий свойства этого кристалла, не должен менять своего вида при этих преобразованиях симметрии, т. е. его компоненты не должны меняться.
- Инверсия (i): (x, y, z) ->(-x, -y, -z) Симметрия кристалла накладывает ограничение на вид любого тензора, описывающего свойства: если преобразованиях симметрии направлений направления в кристалле переходят в эквивалентные, то и тензор, характеризующий свойства этого кристалла, не должен менять своего вида при этих преобразованиях симметрии, т. е. его компоненты не должны меняться.
 Преобразования координат группы куба (Oh) При определенном выборе системы координат (оси направлены вдоль ребер, а центр совпадает с центром инверсии) точечным преобразованиям группы Oh соответствуют все перестановки координат с любыми изменениями знаков, например: (x, y, z)→ (–x, –y, –z) — инверсия, (x, y, z)→ (y, –x, z) – поворот C 4 вокруг оси z (x, y, z)→ (y, z, x) — поворот C 3, -------------------------------Всего 48 = 3!· 23, где 3! — число возможных перестановок, 23 — число возможных расстановок знаков. Возьмем преобразование, при котором координаты x и y меняются местами: (x, y, z)→ (y, x, z). При этом преобразовании σxx→σyy. Т. к. компоненты тензора кристалла класса Oh не должны меняться при всех преобразованиях симметрии группы куба, то получаем что σxx = σyy. Аналогично доказывается, что σxx = σzz и σyy = σzz.
Преобразования координат группы куба (Oh) При определенном выборе системы координат (оси направлены вдоль ребер, а центр совпадает с центром инверсии) точечным преобразованиям группы Oh соответствуют все перестановки координат с любыми изменениями знаков, например: (x, y, z)→ (–x, –y, –z) — инверсия, (x, y, z)→ (y, –x, z) – поворот C 4 вокруг оси z (x, y, z)→ (y, z, x) — поворот C 3, -------------------------------Всего 48 = 3!· 23, где 3! — число возможных перестановок, 23 — число возможных расстановок знаков. Возьмем преобразование, при котором координаты x и y меняются местами: (x, y, z)→ (y, x, z). При этом преобразовании σxx→σyy. Т. к. компоненты тензора кристалла класса Oh не должны меняться при всех преобразованиях симметрии группы куба, то получаем что σxx = σyy. Аналогично доказывается, что σxx = σzz и σyy = σzz.
 Рассмотрим другое преобразование группы куба: (x, y, z)→ (–x, y, z): σxy→–σxy. Отсюда следует, что σxy = 0. Аналогично доказывается, что равны нулю все недиагональные компоненты тензора. Недиагональные компоненты любого тензора второго ранга, характеризующего свойства кристалла класса Oh, равны нулю, а диагональные равны между собой, т. е. тензор превращается в скаляр. Закон Ома для кристалла группы Oh имеет вид:
Рассмотрим другое преобразование группы куба: (x, y, z)→ (–x, y, z): σxy→–σxy. Отсюда следует, что σxy = 0. Аналогично доказывается, что равны нулю все недиагональные компоненты тензора. Недиагональные компоненты любого тензора второго ранга, характеризующего свойства кристалла класса Oh, равны нулю, а диагональные равны между собой, т. е. тензор превращается в скаляр. Закон Ома для кристалла группы Oh имеет вид:
 Элементы континуальной теории упругости (L&L, том 7, глава 1, п. 1 -2) Под влиянием приложенных сил твердые тела деформируются, т. е. меняют форму и объем. Характер деформации зависит от величины силы: - область упругих деформаций - деформации обратимы, связь деформации и силы линейная (выполняется закон Гука); - область пластических деформаций - деформации необратимы, закон Гука не выполняется; - область разрушений - образец разъединяется на части. Теория упругости работает в области упругих деформаций и рассматривает твердые тела как сплошные среды "Одномерный" закон Гука: Упругая энергия: F - сила, - растяжение, k - коэффициент упругости
Элементы континуальной теории упругости (L&L, том 7, глава 1, п. 1 -2) Под влиянием приложенных сил твердые тела деформируются, т. е. меняют форму и объем. Характер деформации зависит от величины силы: - область упругих деформаций - деформации обратимы, связь деформации и силы линейная (выполняется закон Гука); - область пластических деформаций - деформации необратимы, закон Гука не выполняется; - область разрушений - образец разъединяется на части. Теория упругости работает в области упругих деформаций и рассматривает твердые тела как сплошные среды "Одномерный" закон Гука: Упругая энергия: F - сила, - растяжение, k - коэффициент упругости
 Тензор деформаций Пусть до деформации координаты некоторой точки были r с компонентами x 1=x, x 2=y, x 3=z, а после деформации стали r' с копмонентами xi'. Смещение точки тела при деформации изобразится вектором u=r'-r - вектор деформации (или вектор смещения) Задание вектора деформации как функции координат полностью определяет деформацию тела. Но этот же вектор описывает и смещение тела как целое. Поэтому деформацию в точке с координатами (x 1, x 2, x 3) описывают как изменение расстояния между бесконечно близкими точками вблизи этой координаты. Пусть до деформации это расстояние было Далее будем подразумевать суммирование по повторяющимся индексам в каждом сомножителе выражения. Тогда:
Тензор деформаций Пусть до деформации координаты некоторой точки были r с компонентами x 1=x, x 2=y, x 3=z, а после деформации стали r' с копмонентами xi'. Смещение точки тела при деформации изобразится вектором u=r'-r - вектор деформации (или вектор смещения) Задание вектора деформации как функции координат полностью определяет деформацию тела. Но этот же вектор описывает и смещение тела как целое. Поэтому деформацию в точке с координатами (x 1, x 2, x 3) описывают как изменение расстояния между бесконечно близкими точками вблизи этой координаты. Пусть до деформации это расстояние было Далее будем подразумевать суммирование по повторяющимся индексам в каждом сомножителе выражения. Тогда:
 после деформации: , где Тогда: или , где - тензор деформации Тензор деформации по определению симметричен Теорема Любой симметричный тензор можно привести к главным осям, то есть выбрать систему координат, в которой тензор - диагонален.
после деформации: , где Тогда: или , где - тензор деформации Тензор деформации по определению симметричен Теорема Любой симметричный тензор можно привести к главным осям, то есть выбрать систему координат, в которой тензор - диагонален.
 Если тензор деформации в данной точке привести к главным осям, то вблизи этой точки элемент длины после деформации имеет вид: ε(i)=εii - главные значения тензора Деформацию в каждом элементе объема тела можно рассматривать как совокупность трех независимых деформаций по трем взаимноперпендикулярным направлениям - главным осям тензора деформаций Каждая из этих деформаций представляет собой простое растяжение (или сжатие) вдоль соответствующего направления. Например, длина dx 1 превращается в длину Величины относительные удлинения представляют собой вдоль соответствующих осей
Если тензор деформации в данной точке привести к главным осям, то вблизи этой точки элемент длины после деформации имеет вид: ε(i)=εii - главные значения тензора Деформацию в каждом элементе объема тела можно рассматривать как совокупность трех независимых деформаций по трем взаимноперпендикулярным направлениям - главным осям тензора деформаций Каждая из этих деформаций представляет собой простое растяжение (или сжатие) вдоль соответствующего направления. Например, длина dx 1 превращается в длину Величины относительные удлинения представляют собой вдоль соответствующих осей
 Случай малых деформаций тензор деформаций в пренебрежении членами второго порядка малости С точностью до величин высшего порядка относительные удлинения элементов длины вдоль направлений главных осей тензора деформации равны главным значениям этого тензора
Случай малых деформаций тензор деформаций в пренебрежении членами второго порядка малости С точностью до величин высшего порядка относительные удлинения элементов длины вдоль направлений главных осей тензора деформации равны главным значениям этого тензора
 Изменение объема при малых деформациях d. V - элемент объема вблизи точки (x 1, x 2, x 3). Вычислим объем этого элемента после деформирования d. V', используя в качестве осей координат главные оси тензора деформации в этой точке. Теорема сумма диагональных компонент (след, шпур) тензора не зависит от системы координат относительное изменение объема равно сумме диагональных компонент тензора деформации
Изменение объема при малых деформациях d. V - элемент объема вблизи точки (x 1, x 2, x 3). Вычислим объем этого элемента после деформирования d. V', используя в качестве осей координат главные оси тензора деформации в этой точке. Теорема сумма диагональных компонент (след, шпур) тензора не зависит от системы координат относительное изменение объема равно сумме диагональных компонент тензора деформации
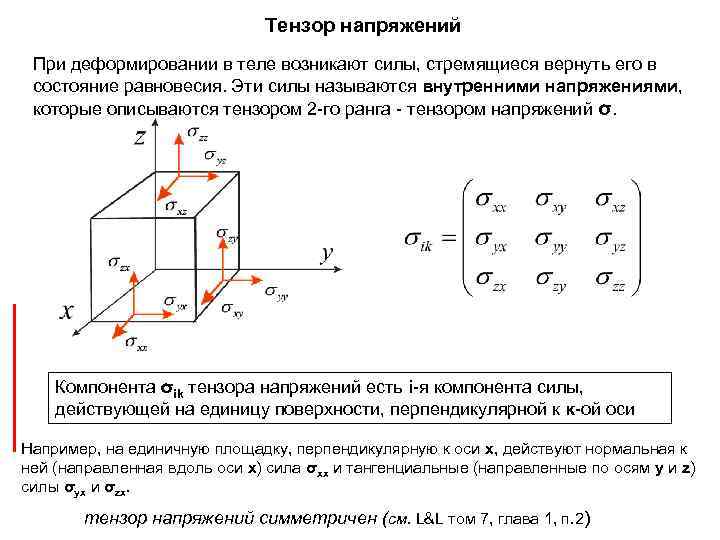 Тензор напряжений При деформировании в теле возникают силы, стремящиеся вернуть его в состояние равновесия. Эти силы называются внутренними напряжениями, которые описываются тензором 2 -го ранга - тензором напряжений σ. Компонента σik тензора напряжений есть i-я компонента силы, действующей на единицу поверхности, перпендикулярной к к-ой оси Например, на единичную площадку, перпендикулярную к оси x, действуют нормальная к ней (направленная вдоль оси x) сила σxx и тангенциальные (направленные по осям y и z) силы σyx и σzx. тензор напряжений симметричен (см. L&L том 7, глава 1, п. 2)
Тензор напряжений При деформировании в теле возникают силы, стремящиеся вернуть его в состояние равновесия. Эти силы называются внутренними напряжениями, которые описываются тензором 2 -го ранга - тензором напряжений σ. Компонента σik тензора напряжений есть i-я компонента силы, действующей на единицу поверхности, перпендикулярной к к-ой оси Например, на единичную площадку, перпендикулярную к оси x, действуют нормальная к ней (направленная вдоль оси x) сила σxx и тангенциальные (направленные по осям y и z) силы σyx и σzx. тензор напряжений симметричен (см. L&L том 7, глава 1, п. 2)
 Простые деформации: изотропные твердые тела Равномерное всестороннее (гидростатическое) сжатие - на каждую точку поверхности тела действует одинаковое по величине давление, направленное везде по нормали к поверхности внутрь объема тела. Тангенциальных напряжений нет, все отличные от нуля компоненты равны давлению p: Всестороннее сжатие сопровождается изменением объема без изменения формы. Деформация сдвига - объем тела остается неизменным, меняется только его форма (εii=0) Всякую деформацию можно представить в виде суммы деформаций чистого сдвига и всестороннего сжатия: сдвиг сжатие
Простые деформации: изотропные твердые тела Равномерное всестороннее (гидростатическое) сжатие - на каждую точку поверхности тела действует одинаковое по величине давление, направленное везде по нормали к поверхности внутрь объема тела. Тангенциальных напряжений нет, все отличные от нуля компоненты равны давлению p: Всестороннее сжатие сопровождается изменением объема без изменения формы. Деформация сдвига - объем тела остается неизменным, меняется только его форма (εii=0) Всякую деформацию можно представить в виде суммы деформаций чистого сдвига и всестороннего сжатия: сдвиг сжатие
 Свободная энергия деформации изотропного твердого тела Можно показать: Из компонент симметричного тензора можно составить два независимых скаляра второй степени Разложение удельной энергии (скаляра) с точностью до членов второго порядка по элементам тензора деформации можно представить в виде суммы квадратов компонент "сдвига" и "всестороннего сжатия" К - модуль всестороннего сжатия μ - модуль сдвига Закон Гука для изотропного твердого тела: обратная формула:
Свободная энергия деформации изотропного твердого тела Можно показать: Из компонент симметричного тензора можно составить два независимых скаляра второй степени Разложение удельной энергии (скаляра) с точностью до членов второго порядка по элементам тензора деформации можно представить в виде суммы квадратов компонент "сдвига" и "всестороннего сжатия" К - модуль всестороннего сжатия μ - модуль сдвига Закон Гука для изотропного твердого тела: обратная формула:
 Однородные деформации Деформации, при которых тензор деформации постоянен по всему объему тела. Примеры: - всестороннее сжатие - простое растяжение (или сжатие) стержня (стенки свободны) - одностороннее сжатие (стенки зафиксированы) Простое растяжение: Силы действуют равномерно на поверхности концов стержня (вдоль оси z), p - сила, действующая на единицу поверхности. , остальные элементы тензора напряжений равны нулю - относительное растяжение стержня вдоль z E - модуль растяжения (модуль Юнга), 1/E - коэффициент растяжения относительное сжатие в поперечном направлении σ - коэффициент Пуассона
Однородные деформации Деформации, при которых тензор деформации постоянен по всему объему тела. Примеры: - всестороннее сжатие - простое растяжение (или сжатие) стержня (стенки свободны) - одностороннее сжатие (стенки зафиксированы) Простое растяжение: Силы действуют равномерно на поверхности концов стержня (вдоль оси z), p - сила, действующая на единицу поверхности. , остальные элементы тензора напряжений равны нулю - относительное растяжение стержня вдоль z E - модуль растяжения (модуль Юнга), 1/E - коэффициент растяжения относительное сжатие в поперечном направлении σ - коэффициент Пуассона
 Для изотропного стержня:
Для изотропного стержня:
 Контрольные вопросы 1. Что такое физический тензор? 2. Что определяет ранг тензора? 3. Что определяет мерность тензора? 4. Как количество компонент тензора выражается через его ранг и мерность? 5. Как при преобразовании системы координат меняется тензор нулевого ранга? 6. Как при преобразовании системы координат меняется тензор первого ранга? 7. Как при преобразовании системы координат меняется тензор произвольного ранга? 8. Какова матрица, описывающая преобразование координат при операции инверсии относительно нуля? 9. Какова матрица, описывающая преобразование координат при отражении в плоскости, проходящей через начало координат перпендикулярно оси x? 10. Какова матрица, описывающая преобразование координат при повороте C 4 вокруг оси z?
Контрольные вопросы 1. Что такое физический тензор? 2. Что определяет ранг тензора? 3. Что определяет мерность тензора? 4. Как количество компонент тензора выражается через его ранг и мерность? 5. Как при преобразовании системы координат меняется тензор нулевого ранга? 6. Как при преобразовании системы координат меняется тензор первого ранга? 7. Как при преобразовании системы координат меняется тензор произвольного ранга? 8. Какова матрица, описывающая преобразование координат при операции инверсии относительно нуля? 9. Какова матрица, описывающая преобразование координат при отражении в плоскости, проходящей через начало координат перпендикулярно оси x? 10. Какова матрица, описывающая преобразование координат при повороте C 4 вокруг оси z?
 11. Ранг тензора проводимости? Тензорный вид закона ома? 12. Как меняются компоненты тензора при преобразовании системы координат, соответствующим элементу группы симметрии направлений кристалла? 13. Как меняются компоненты тензора второго ранга при преобразовании системы координат, соответствующим операции инверсии относительно нуля? 14. Какие преобразования координат соответствуют точечным преобразованиям группы Oh при определенном выборе системы координат (оси направлены вдоль ребер, а центр совпадает с центром инверсии)? 15. Сколько различных ненулевых компонент имеет тензор 2 -го ранга, описывающий некоторое свойство кубического кристалла (группа Oh)? 16. Определение областей упругих деформаций, пластических деформаций и области разрушений. 17. Общее определение тензора деформаций 18. Определение тензора деформаций для случая малых деформаций
11. Ранг тензора проводимости? Тензорный вид закона ома? 12. Как меняются компоненты тензора при преобразовании системы координат, соответствующим элементу группы симметрии направлений кристалла? 13. Как меняются компоненты тензора второго ранга при преобразовании системы координат, соответствующим операции инверсии относительно нуля? 14. Какие преобразования координат соответствуют точечным преобразованиям группы Oh при определенном выборе системы координат (оси направлены вдоль ребер, а центр совпадает с центром инверсии)? 15. Сколько различных ненулевых компонент имеет тензор 2 -го ранга, описывающий некоторое свойство кубического кристалла (группа Oh)? 16. Определение областей упругих деформаций, пластических деформаций и области разрушений. 17. Общее определение тензора деформаций 18. Определение тензора деформаций для случая малых деформаций
 19. Какую физическую величину определяют главные значения тензора деформаций? (для случая малых деформаций) 20. Как относительное изменение объема тела выражается через компоненты тензора деформации 21. Определение тензора напряжений 22. Какой вид имеет тензор напряжений для деформации всестороннего сжатия изотропного твердого тела? 23. Как меняется объем тела при деформации чистого сдвига? 24. Сколько независимых констант нужно использовать для описания упругих свойств изотропного твердого тела? 25. Что такое однородная деформация? Примеры? 26. Что такое модуль Юнга? 27. Что такое коэффициент Пуассона?
19. Какую физическую величину определяют главные значения тензора деформаций? (для случая малых деформаций) 20. Как относительное изменение объема тела выражается через компоненты тензора деформации 21. Определение тензора напряжений 22. Какой вид имеет тензор напряжений для деформации всестороннего сжатия изотропного твердого тела? 23. Как меняется объем тела при деформации чистого сдвига? 24. Сколько независимых констант нужно использовать для описания упругих свойств изотропного твердого тела? 25. Что такое однородная деформация? Примеры? 26. Что такое модуль Юнга? 27. Что такое коэффициент Пуассона?
 ЗАДАЧИ старые нерешенные Лекция 2: 4. Вычислить относительную долю пространства, заполненного сферами, в следующих структурах: а) простая кубическая структура; б) ОЦК структура; в) ГЦК структура: 5. Проанализировать наличие эквивалентных плоскостей и осей в группах Сnv, Dn, Td (два элемента симметрии эквивалентны, если в группе существует преобразование, переводящее их друг в друга) Лекция 3: 3. Сколько существует различных двумерных решеток Браве? Перечислить. Обосновать.
ЗАДАЧИ старые нерешенные Лекция 2: 4. Вычислить относительную долю пространства, заполненного сферами, в следующих структурах: а) простая кубическая структура; б) ОЦК структура; в) ГЦК структура: 5. Проанализировать наличие эквивалентных плоскостей и осей в группах Сnv, Dn, Td (два элемента симметрии эквивалентны, если в группе существует преобразование, переводящее их друг в друга) Лекция 3: 3. Сколько существует различных двумерных решеток Браве? Перечислить. Обосновать.
 ЗАДАЧИ новые 1. * Доказать правило перемножения значков для тензоров второго ранга
ЗАДАЧИ новые 1. * Доказать правило перемножения значков для тензоров второго ранга


