Лекция 4 1 Содержание предыдущей лекции Динамика

Лекция 4 1

Содержание предыдущей лекции Динамика поступательного движения. Закон сохранения импульса. • Движение тел переменной массы. Формула Циолковского. Механическая энергия • Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией. • Консервативные и неконсервативные силы. • Работа и кинетическая энергия. • Закон сохранения полной механической энергии в поле потенциальных сил. 2

Контрольный вопрос В изолированной системе сохраняется: а) кинетическая энергия, б) потенциальная энергия, в) сумма кинетической и потенциальной энергий, г) как кинетическая, так и потенциальная энергии. Закон сохранения полной механической энергии: в изолированной системе сохраняется сумма кинетической и потенциальной энергий. в) 3

Содержание сегодняшней лекции Механическая энергия • Столкновение тел. Кинематика и динамика вращательного движения • Кинематика вращательного движения: угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением. • Момент силы. Уравнение моментов. Момент инерции. Теорема Штейнера. Кинетическая энергия вращательного движения твердого тела. 4

Столкновение тел Два крайних случая соударения – абсолютно упругий и абсолютно неупругий удары. 5

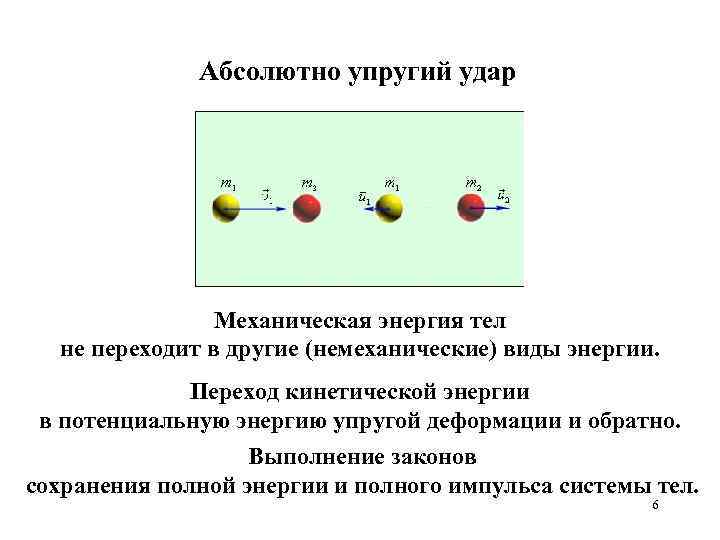Абсолютно упругий удар Механическая энергия тел не переходит в другие (немеханические) виды энергии. Переход кинетической энергии в потенциальную энергию упругой деформации и обратно. Выполнение законов сохранения полной энергии и полного импульса системы тел. 6

Абсолютно упругий удар Две частицы образуют замкнутую систему. Отсутствие вращения шаров. Закон сохранения механической энергии Закона сохранения суммарного импульса частиц 7

Абсолютно упругий удар 8

Абсолютно упругий удар m 2 m + 1 9

Абсолютно неупругий удар Потенциальная энергия деформации не возникает. Полное или частичное превращение кинетической энергии во внутреннюю энергию. После удара: движение тел с одинаковой скоростью или их нахождение в состоянии покоя. 10

Абсолютно неупругий удар Выполнение закона сохранения импульса. Невыполнение закона сохранения механической энергии. Выполнение закона сохранения суммарной энергии различных видов - механической и внутренней. 11

Абсолютно неупругий удар Закон сохранения суммарного импульса двух частиц, образующих замкнутую систему до удара после удара 12

Вращательное движение 13

Вращательное движение – движение, при котором все точки тела совершают движение по концентрическим окружностям. 14

Кинематика вращательного движения Вектор характеристика поворота материальной точки (тела) на некоторый угол относительно некоторой фиксированной в пространстве оси. Длина вектора – угол поворота. Направление вектора – ориентация оси. Неоднозначность в выборе направления поворота – поворот возможен по или против часовой стрелки. 15

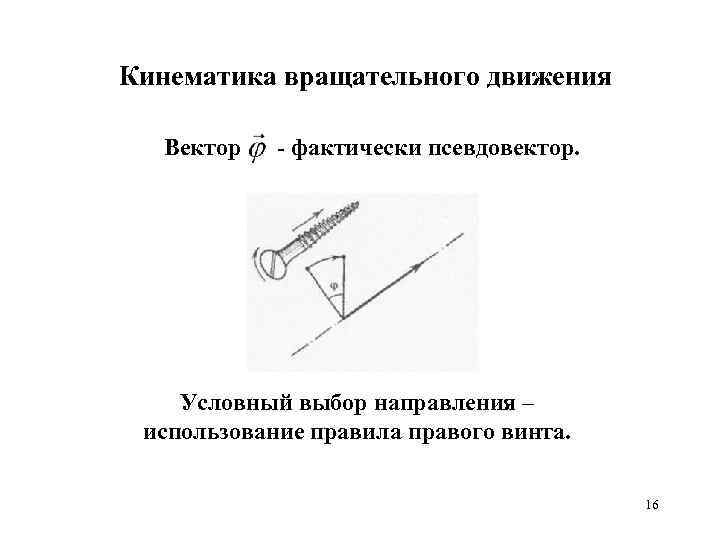Кинематика вращательного движения Вектор - фактически псевдовектор. Условный выбор направления – использование правила правого винта. 16

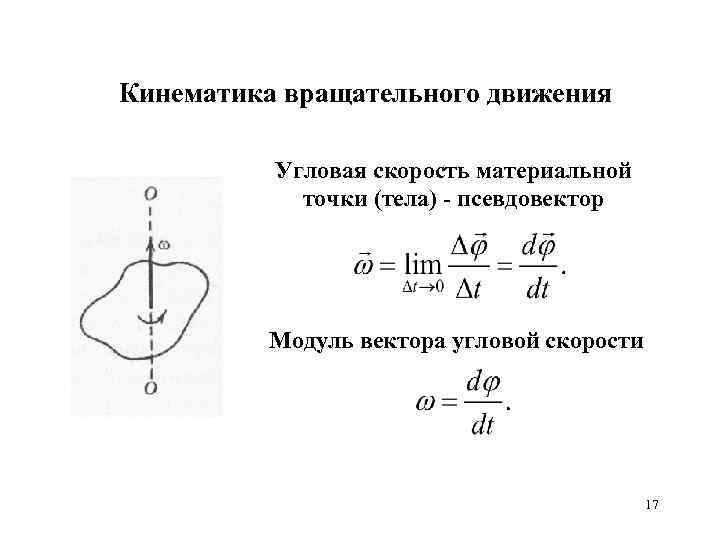Кинематика вращательного движения Угловая скорость материальной точки (тела) - псевдовектор Модуль вектора угловой скорости 17

Кинематика вращательного движения Равномерное вращательное движение – вращение с постоянной скоростью Период обращения Т при равномерном вращении – время, за которое тело делает один оборот. Число оборотов в единицу времени Угловая скорость 18

Кинематика вращательного движения Возможность изменения за счет изменения скорости вращения тела вокруг оси (модуль) и за счет поворота оси (направление). Угловое ускорение (псевдовектор) - характеристика скорости изменения вектора угловой скорости во времени. 19

Кинематика вращательного движения Разная линейная скорость у различных точек вращающегося тела. 20

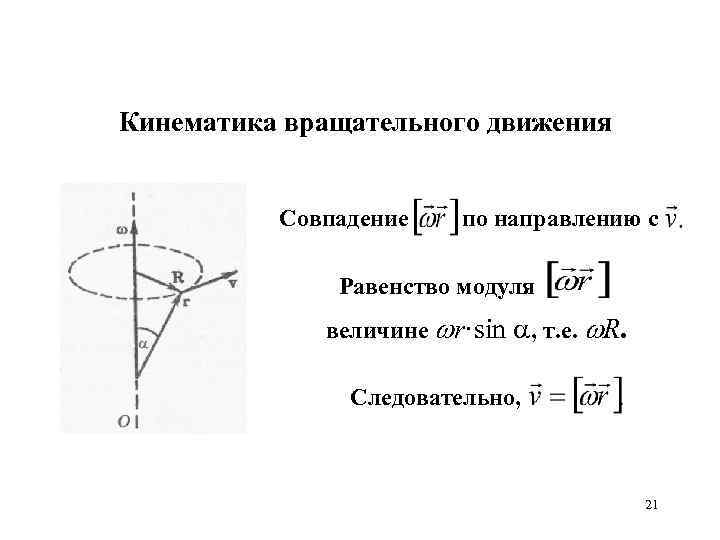Кинематика вращательного движения Совпадение по направлению с Равенство модуля величине r·sin , т. е. R. Следовательно, 21

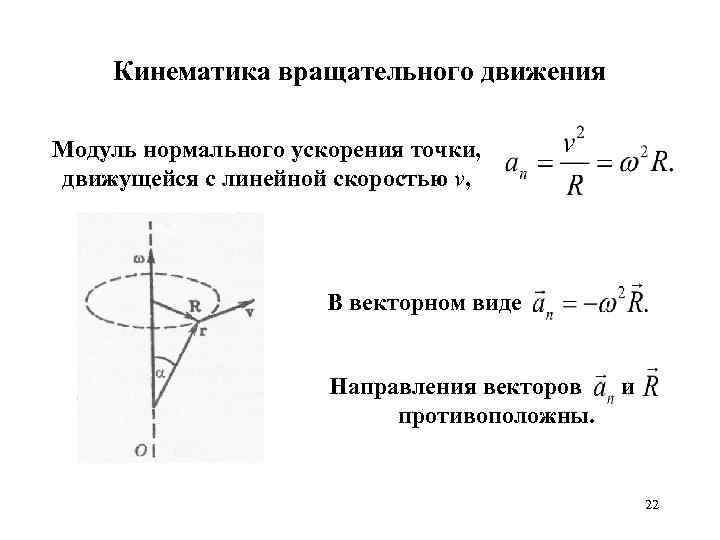Кинематика вращательного движения Модуль нормального ускорения точки, движущейся с линейной скоростью v, В векторном виде Направления векторов противоположны. и 22

Кинематика вращательного движения Пусть ось тела не поворачивается в пространстве. Модуль тангенциального ускорения Линейная скорость точки на расстоянии R от оси вращения 23

Динамика вращательного движения 24

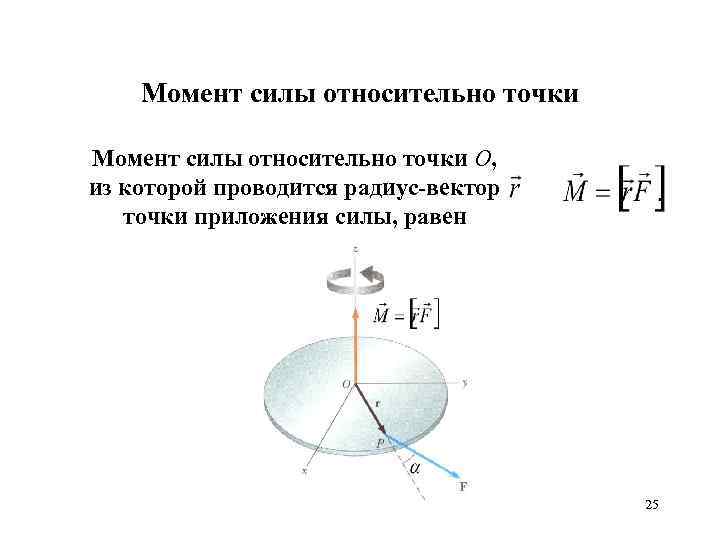Момент силы относительно точки О, из которой проводится радиус-вектор точки приложения силы, равен 25

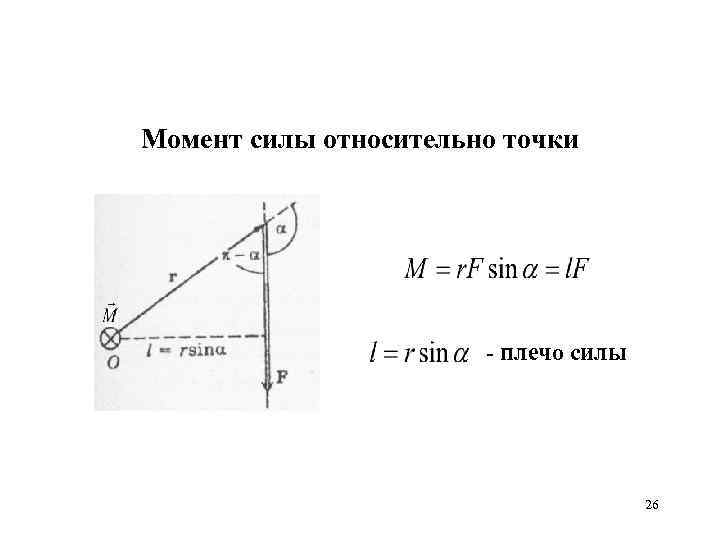Момент силы относительно точки - плечо силы 26

Момент силы относительно оси Момент силы относительно точки – характеристика способности силы вращать тело вокруг точки, относительно которой он берется. Возможность произвольного вращения тела относительно точки О. 27

Момент силы относительно оси Результат: поворот тела под действием силы вокруг оси, перпендикулярной к плоскости, в которой лежат сила F и точка О, т. е. вокруг оси, совпадающей с направлением момента силы относительно данной точки. 28

Момент силы относительно оси Проекция вектора на некоторую ось, проходящую через точку О, относительно которой определен вектор называется моментом силы относительно этой оси: 29

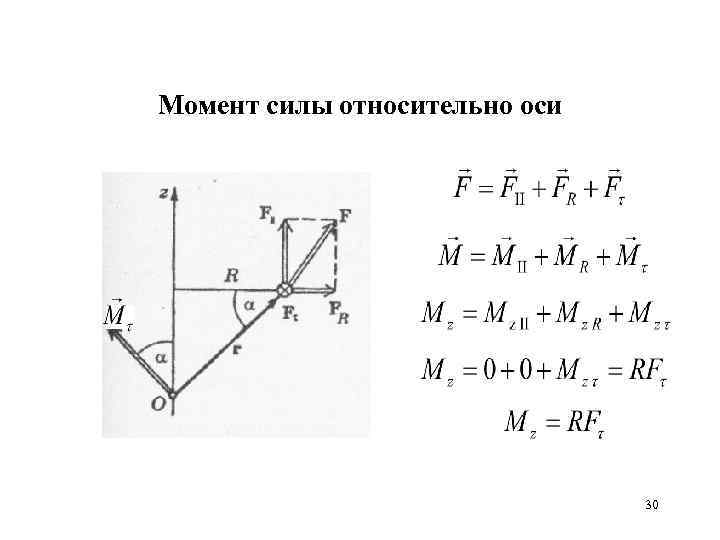Момент силы относительно оси 30

Момент силы относительно оси z – характеристика способности силы вращать тело вокруг этой оси. Поворот тем успешнее, чем больше тангенциальная составляющая силы и плечо R. 31

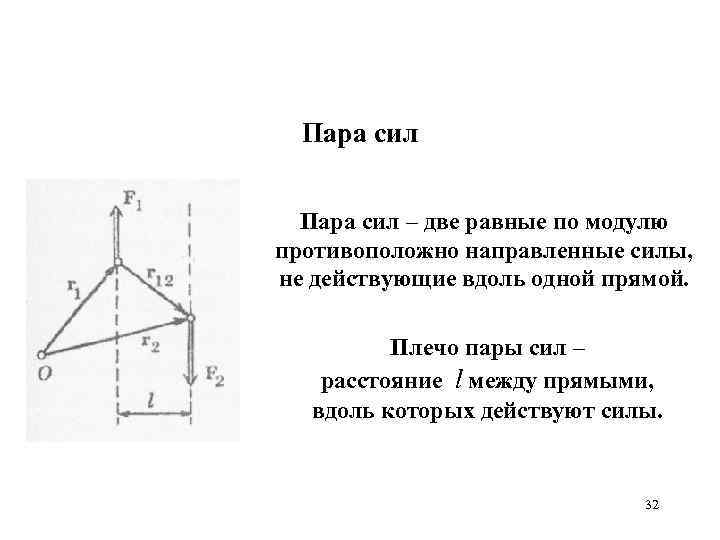Пара сил – две равные по модулю противоположно направленные силы, не действующие вдоль одной прямой. Плечо пары сил – расстояние l между прямыми, вдоль которых действуют силы. 32

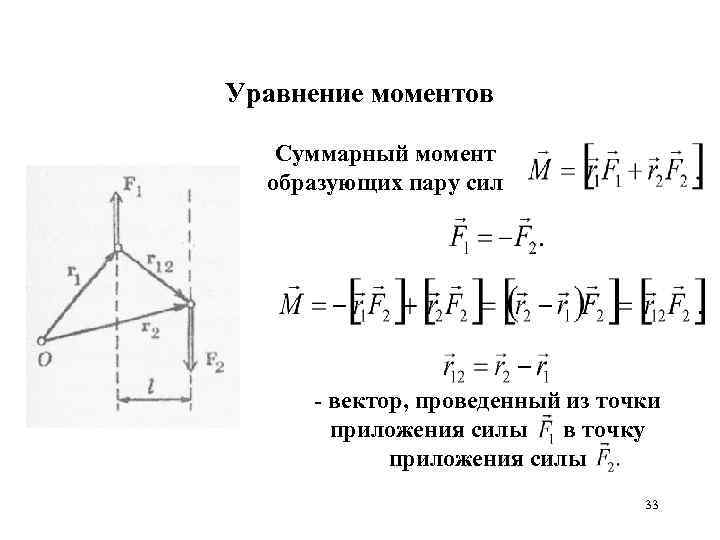Уравнение моментов Суммарный момент образующих пару сил - вектор, проведенный из точки приложения силы в точку приложения силы 33

Уравнение моментов Независимость выражения от выбора точки О. Следствие: момент пары сил относительно любой точки одинаков. 34

Уравнение моментов Направление вектора момента пары сил – перпендикулярное плоскости, в которой лежат силы. Численное значение вектора момента пары сил – произведение модуля любой из сил на плечо. 35

Уравнение моментов Действие сил взаимодействия между частицами вдоль одной и той же прямой. Равенство по модулю и противоположное направление вдоль одной и той же прямой моментов сил взаимодействия относительно произвольной точки О. Уравновешивание моментов внутренних сил другом, в частности, для твердого тела 36

Момент инерции Абсолютно твердое тело – система частиц (материальных точек) с неизменным расстоянием между ними. Момент инерции тела относительно некоторой оси – величина, равная сумме произведений элементарных масс, из которых состоит данное тело, на квадраты их расстояний от некоторой оси, Момент инерции тела равен сумме моментов инерции его частей. 37

Момент инерции Плотность тела – характеристика распределения массы m в его объеме V, Плотность неоднородного тела 38

Момент инерции Если = соnst, то Наиболее точное решение 39

Теорема Штейнера Момент инерции I относительно произвольной оси равен сумме моментов инерции IC относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния а между осями: 40

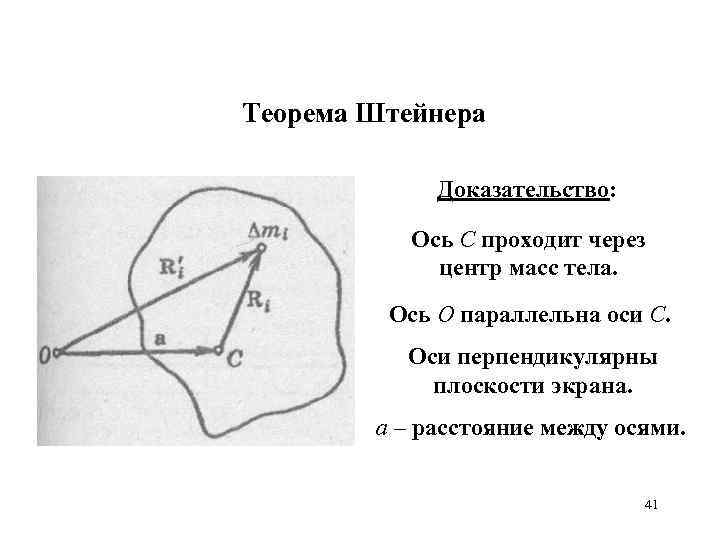Теорема Штейнера Доказательство: Ось С проходит через центр масс тела. Ось О параллельна оси С. Оси перпендикулярны плоскости экрана. а – расстояние между осями. 41

Теорема Штейнера - ось С проходит через центр масс. 42

Кинетическая энергия вращательного движения твердого тела Вращение тела вокруг неподвижной оси z. Кинетическая энергия i-й элементарной массы Кинетическая энергия тела вращающегося вокруг неподвижной оси 43

Контрольный вопрос Две частицы обладают одинаковыми кинетическими энергиями. Величины их импульсов соотносятся как: а) p 1 < p 2, б) p 1 = p 2, в) p 1 > p 2, г) невозможно определить. 44