Лекция 37 Модель и методика расчета кинетики докритического

Лекция 37. Модель и методика расчета кинетики докритического псевдохрупкого роста трещин и построения G – V диаграмм с использованием подходов ЛУМР и термофлуктуационной теории долговечности для стеклообразных полимеров при статических нагрузках Общие подходы. В данном разделе рассмотрены: модель докритического роста магистральной трещины в псевдохрупком материале и полуэмпирическая методика с использованием макро- и микроподходов механики трещин и кинетической теории долговечности, позволяющие при совместном использовании построить G – V диаграммы и оценить кинетику докритического роста трещин в стеклообразных полимерах и клеевых соединениях. Применение макроподхода линейной механики разрушения (ЛУМР) для анализа нагружения и псевдохрупкого роста трещины в квазиупругом теле с трещиной базируется на представлении об упругом поведении тела в целом, а микроподхода - о развитии неупругих деформаций только в локальной зоне вблизи вершины трещины, размер которой значительно меньше размера трещины. Это позволяет использовать основные соотношения ЛУМР для расчета трещинодвижущих сил и определения критериев и условий инициирования и роста трещины с учетом геометрии тела с трещиной, типа и условий нагружения. Как было показано выше, применительно к стеклообразным полимерам, к которым относятся большинство отвержденных густосетчатых полимеров, в том числе эпоксидных, а также к ПКМ и клеевым композициям на их основе, наиболее эффективной моделью локальной неупругой зоны вблизи вершины псевдохрупкой трещины является модель Баренблатта-Дагдейла. В этой модели неупругая зона вблизи вершины трещины рассматривается как продолжение трещины, противоположные поверхности которой связаны силами когезии c, равными предельному напряжению неупругих деформаций, а ее основные геометрические параметры (длина зоны l и ее предельное локальное раскрытие ) связаны с трещинодвижущими силами (GI и KI), упругими константами тела (модулями Юнга Е и сдвига ) и соответствующими соотношениями.

Критические условия инициирования и роста трещины в модели Баренблатта-Дагдейла определяются как традиционными для ЛУМР энергетическими и силовыми критериями, так и локальными (микромеханическими) деформационными параметрами. Макромеханические критерии инициирования и роста трещины соответствуют достижению параметрами трещинодвижущей силы, определяемыми нагрузкой на тело с дефектом и его геометрией, своих предельных значений, равных сопротивлению трещины (GI=GIC, KI=KIC). Микромеханические критерии инициирования и роста трещины соответствуют достижению геометрическими параметрами локальной зоны неупругих деформаций своих предельных значений (l=l. C, = c), зависящих от предельной деформируемости материала. Если глобальная нагрузка на трещину и локальная деформация неупругой зоны меньше предельной (GI GIC, KI KIC, l l. C, c), то быстрый (критический) рост трещины не может происходить и возможно только ее медленное докритическое подрастание в результате процессов, протекающих в неупругой зоне вблизи вершины трещины и уменьшающих сопротивление ее росту. В рассматриваемой модели при любой нагрузке на трещину, меньшей критической, локальная зона неупругих деформаций развивается практически мгновенно по псевдопластическому механизму (вынужденной высокоэластичности) в виде микрокрейз (под действием растягивающих напряжений) или локальных полос сдвига (под действием сдвиговых напряжений) и сопровождается ориентационной вытяжкой полимерных цепей. В этой зоне на псевдопластически деформированный полимер действует постоянное локальное напряжение, равное предельному напряжению неупругих деформаций c, обусловленному действием когезионных внутри- и межмолекулярных связей.

Докритическое подрастание трещины при отсутствии глобальных условий ее критического роста возможно как результат достижения локальных критических условий в неупругой зоне вследствие ослабления во времени когезионных сил и развития предельных деформаций из-за разрыва внутри- и межмолекулярных связей, в частности, по термофлуктуационному механизму, описываемому в теории долговечности и длительной прочности полимеров, так и в результате воздействия агрессивных сред (реагентов) и излучений. Для описания зависимости c от времени (t) вследствие термофлуктуационного механизма ослабления когезионных сил используется, ранее приведенное, уравнение кинетической теории прочности полимеров (Журкова), которое базируется на представлении о решающей роли в разрушении полимера при длительном действии малых нагрузок активационных (термофлуктуационных) процессов накопления повреждений на молекулярном уровне, аналогичных химическим реакциям и проскальзыванию цепей: Из уравнения Журкова при достижении локального предела вынужденной эластичности может быть получено выражение для зависимости с от времени: Используя это соотношение, а также макро- и микромеханические соотношения ЛУМР, связывающие нагрузку Р на образец с трещиной или смещение (деформацию) в нем с нагрузкой на трещину (GI и KI): (*) и геометрические параметры неупругой зоны вблизи вершины трещины l и с GI или KI и с, можно проанализировать возможности и найти способы расчета кинетики докритического роста трещины при различных типах и условиях нагружения.

Ниже такой анализ проведен для двух основных типов длительного статического нагружения образца с трещиной типа 1. При постоянной нагрузке (Р – 2. При постоянном раскрытии трещины ( - ПДКБ: const); const). За макромеханический параметр трещинодвижущей силы принят энергетический параметр GI в условиях плосконапряженного состояния, а в качестве основной микромеханической характеристики неупругой зоны вблизи вершины трещины – ее максимальное раскрытие . При этом предполагается, что докритический рост трещины происходит тогда, когда величина макромеханического параметра при заданной длине трещины а меньше критической (GI GIС), а микромеханический параметр достигает своего предельного значения ( = с). Достижение трещиной своей критической длины (ас) и, соответственно, критического значения трещинодвижущей силы GIС приводит к критическому росту трещины. Испытание при постоянной нагрузке Постоянная нагрузка на образец (режим ползучести, Р-const, и - функции времени). Начальная длина трещины а 0 ас, раскрытие вершины трещины в ненагруженном образце равно 0. Нагрузка Р Рс прикладывается мгновенно и поддерживается постоянной, обеспечивая начальную нагрузку на трещину GI(0) = GIС и практически мгновенное развитие неупругой зоны вблизи вершины трещины (0) = с Где с(0) – начальный предел текучести (крейзообразования) полимера.

В процессе выдержки под нагрузкой возрастает вследствие уменьшения с в соответствии с вышеприведенным уравнением. За некоторое время, которое можно назвать индукционным периодом (tu) величина достигнет критического значения ( (tu)= с), что соответствует началу докритического подрастания трещины. Этот процесс сопровождается возрастанием макромеханической нагрузки на трещину( ), что делает его нестабильным, и в зависимости от величины нагрузки Р он может достаточно быстро перейти в критическую стадию. Таким образом, при P-const в псевдохрупких стеклообразных полимерах кинетику докритического подрастания трещины теоретически и экспериментально оценить, то есть получить G-V диаграммы, достаточно сложно, так как в течение основного периода времени происходит скрытое развитие неупругой зоны до критических размеров, а процесс докритического подрастания протекает нестабильно, то есть с ускорением. Индукционный период развития неупругой зоны, в решающей степени определяющий долговечность образца с трещиной при P-const, может быть определен из микромеханических условий начала докритического подрастания трещины: = dt = - tdt

Испытание при постоянном раскрытии трещины. Постоянное раскрытие трещины (режим релаксации нагрузки, -const, Р и функции времени). Такой тип нагрузки можно осуществить двояко. В первом случае исходную трещину (ао ас, =0) быстро раскрыть на величину , меньшую критической ( С), и поддерживать ее постоянной. Нагрузка на трещину GI в соответствии с уравнением (*). будет зависеть только от величины и длины трещины а: GI(a) = (**) Начальная величина GI, меньшая GIС при ао ас и С, вызовет практически мгновенное раскрытие зоны неупругих деформаций до начальной величины (0) с. Также как и при первом типе нагружения трещины раскрытие неупругой зоны должно достичь значения с, то есть должен наблюдаться скрытый, индукционный период, рассчитываемый из уравнения (**). Однако, после достижения микромеханического условия докритического подрастания трещины (t) = с, в отличие от Р-const при -const подрастание трещины должно быть стабильным, так как 0. Скорость этого процесса и ее зависимость от G I(а), то есть G-V диаграмма, могут быть рассчитаны из условия: = с использованием соотношений Где: tp = t – tu – время, в течение которого трещина подрастает докритически; t – общее время нагружения; tu индукционный период развития от (0) до с.

Тогда: (***) (****) Очевидно, что необходимость определения и учета индукционного периода докритического развития неупругой зоны затрудняет как расчет, так и экспериментальное определение G-V диаграммы при таком задании постоянного раскрытия трещины. Можно исключить необходимость определения tu. Для этого сразу задают раскрытие трещины, большее или равное критическому ( С) при ее исходной длине ао, и поддерживают -const. Критическое раскрытие трещины вызовет ее быстрое подрастание на некоторую величину а, до тех пор, пока макромеханическая нагрузка на трещину GI(a) не станет меньше GIС, и трещина не остановится. Длина трещины а(0)=ао+ а принимается за начальную, локальное раскрытие неупругой зоны при этом соответствует критической величине (0)= с, и, следовательно, трещина без индукционного периода должна докритически стабильно подрастать. Для оценки скорости этого процесса и построения G-V диаграммы используются вышеприведенные соотношения, в которых tp заменяется на t. Таким образом, методика построения G-V диаграммы при известных параметрах уравнения Журкова (U 0, ), критических параметрах трещиностойкости (GIС, с) и деформационно-прочностных свойствах (Е, с) материала может быть следующей: Ø По формуле (***) рассчитывается зависимость длины трещины от времени для выбранных временных интервалов. Ø По формулам (*) и (****) рассчитываются зависимости GI и V от длины трещины в соответствующие периоды времени. Ø По зависимости G(а) и V(а) строится G-V диаграмма.

Результаты экспериментальных исследований по определению параметров трещиностойкости и построению G – V диаграмм Подходы механики трещин в настоящее время распространяются на исследования ненаполненных термопластов, реактопластов, дисперсно-наполненных и волокнистых материалов с учетом особенностей их релаксационного поведения. В литературе наибольшее количество экспериментально полученных данных о кинетике докритического подрастания трещин и кинетических K-V или G-V диаграмм имеется для хрупких неорганических материалов (металлов, стекол, керамик), подвергающимся коррозионному воздействию окружающей среды, в первую очередь, кислорода и влаги воздуха, а также агрессивных сред. Значительно меньше данных найдено для псевдохрупких полимерных материалов. Линейные (термопластичные) полимеры К настоящему времени наиболее исследовано органическое стекло – полиметилметакрилат (ПММА), которое является очень удобной моделью аморфных стеклообразных полимеров. Эти материалы характеризуют поведение термопластичных материалов под нагрузкой в условии докритического прорастания трещин, и проявляет свойства псевдохрупкого материала при температуре ниже 85 С при практически любых скоростях или длительностях нагружения. Результаты, полученные для ПММА в широком диапазоне температур и сред, хорошо согласуются между собой. На рисунках приведены типичные К-V диаграммы для ПММА при комнатной температуре на воздухе и в воде. Установлено, что с понижением температуры наблюдается уменьшение скорости докритического роста трещины при одинаковой трещинодвижущей силы. Повышение температуры и переход от воздушной среды к жидким средам, наоборот, повышает скорость подрастания трещины при заданной трещинодвижущей силы.

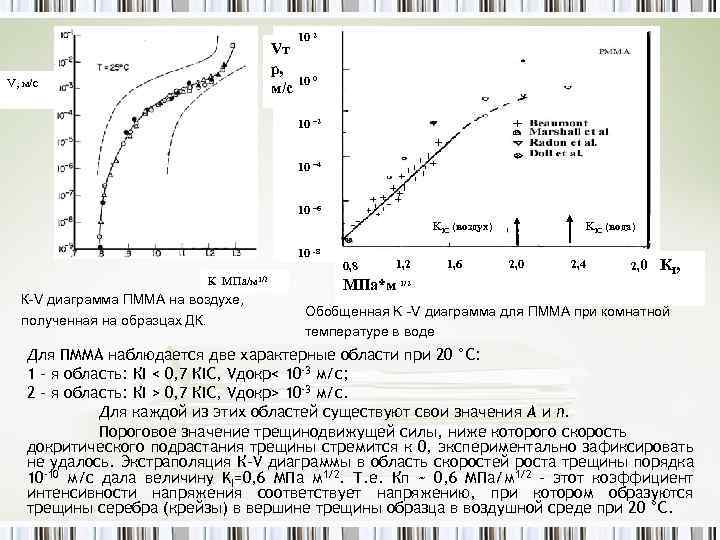10 2 Vт р, 10 0 м/с V, м/c 10 – 2 10 – 4 10 – 6 KIC (воздух) 10 -8 К МПа/м 1/2 К-V диаграмма ПММА на воздухе, полученная на образцах ДК. 0, 8 1, 2 МПа*м 1/2 1, 6 KIC (вода) 2, 0 1, 2 2, 4 1, 6 2, 0 KI, Обобщенная K -V диаграмма для ПММА при комнатной температуре в воде Для ПММА наблюдается две характерные области при 20 °С: 1 – я область: КI < 0, 7 КIC, Vдокр< 10 -3 м/c; 2 - я область: КI > 0, 7 КIC, Vдокр> 10 -3 м/c. Для каждой из этих областей существуют свои значения А и n. Пороговое значение трещинодвижущей силы, ниже которого скорость докритического подрастания трещины стремится к 0, экспериментально зафиксировать не удалось. Экстраполяция К-V диаграммы в область скоростей роста трещины порядка 10 -10 м/с дала величину KI=0, 6 МПа м 1/2. Т. е. Кп ~ 0, 6 МПа/м 1/2 – этот коэффициент интенсивности напряжения соответствует напряжению, при котором образуются трещины серебра (крейзы) в вершине трещины образца в воздушной среде при 20 °С.

Для ПММА K-V–диаграммы получены экспериментально в широком температурном диапазоне (-60 ÷ +80), а также в условиях воздействия на образец различных газообразных и жидких сред. Полученные данные показывают, что при снижении температуры K - V – диаграммы смещаются в область более высоких значений КI, т. е. с уменьшением температуры наблюдается уменьшение скорости докритического роста трещины при одинаковой величине приложенной статистической нагрузки. Такой же эффект проявляется и при переходе от воздушной среды к жидкой среде (вода, этанол, четыреххлористый углерод). Значение коэффициента “n“ при Т = 0÷ 80ºС хорошо коррелирует с обратной величиной тангенса угла механических потерь (tg δ) в области β – релаксации которая определяет докритическое подрастание трещин. При изменении температуры зависимость Vдокр = f(KI) смещается вдоль оси КI в соответствии с уравнением Аррениуса. ΔЕ ≈ 84 к. Дж/мол ≈ ΔЕβ – релаксации т. е. для ПММА Vдокр контролируется β – релаксационным процессом.

Сетчатые полимеры (эпоксидные смолы) Для ненаполненных реактопластов K-V (G-V) – диаграмм получено значительно меньше, причем наибольшее количество имеется для отвержденных эпоксидных смол, поскольку они являются удобной модельной системой. K-V–диаграммы для отвержденных эпоксидных смол получить значительно сложнее, чем для термопластичных материалов (ПММА), т. к. для них практически отсутствует стадия медленного докритического роста трещин при нагружении их вплоть до нагрузки, составляющей 95% от разрушающей. При нагружении стеклоообразных полимеров наблюдается длительный инкубационный период, продолжительность которого определяется величиной приложенной нагрузки. Длина трещины остается постоянной, т. е. не виден ее рост. В этом случае время до разрушения складывается из времени инкубационного периода и времени катастрофического (критического) роста трещин, который составляет долю секунды, при этом порогового безопасного значения не было зафиксировано. Также было показано, что длительная выдержка образца с трещиной при статической нагрузке влияет на величину трещиностойкости при последующем монотонном нагружении. Так выдержка при статической нагрузке более 200 с приводит к увеличению показателя трещиностойкости, а после действия статической нагрузки в течение 107 с показатель трещиностойкости GIС в 2 раза превосходит этот же показатель до приложения нагрузки. Этот эффект, по-видимому, вызван развитием зоны локальных неупругих (вязко -упругих или пластических) деформаций в вершине трещин в процессе выдержки образца при статической нагрузке. С помощью формулы Баренблатта-Дагдейла для расчета размеры зоны локальных неупругих деформаций в вершине трещины (см. выше): Где: σу – предел упругости;

Было рассчитано, что спустя 5∙ 107 с под действием статической нагрузки величина lну достигает 16, 5 мм, по сравнению с 5 мм этой зоны до приложения статической нагрузки. Полученные данные свидетельствуют о медленном развитии локальных неупругих деформаций в отвержденных эпоксидных смолах, что обусловлено медленными релаксационными процессами и скорее всего связано с α–релаксационным процессом (вынужденной сменой конформаций при сегментальном движении). Таким образом, можно предположить, что для отвержденных эпоксидных смол докритическое подрастание трещин лимитируется α–релаксационным процессом, что проявляется в различном поведении при статическом нагружении образцов с трещинами густосетчатых эпоксидных смол и образцов ПММА, в которых Vдокр контролируется β– релаксационным процессом. Для сетчатых эпоксидных смол целесообразно использовать методику построения K-V–диаграмм, в которых постоянной является не нагрузка, а величина раскрытия трещины, которая описана выше. О кинетике докритического роста трещины для густосетчатых полимеров в литературе данных имеется очень мало и они отличаются противоречивостью. Пример полученных при этом диаграмм приведен на рисунке.

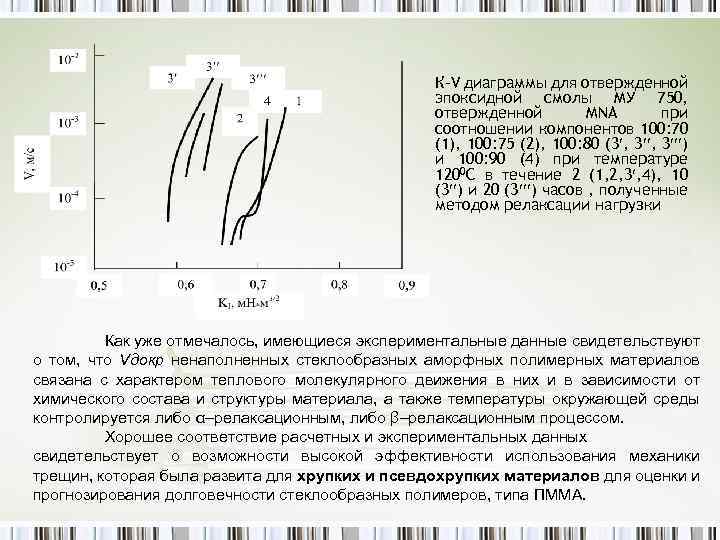К-V диаграммы для отвержденной эпоксидной смолы МУ 750, отвержденной MNA при соотношении компонентов 100: 70 (1), 100: 75 (2), 100: 80 (3 , 3 ) и 100: 90 (4) при температуре 1200 С в течение 2 (1, 2, 3 , 4), 10 (3 ) и 20 (3 ) часов , полученные методом релаксации нагрузки Как уже отмечалось, имеющиеся экспериментальные данные свидетельствуют о том, что Vдокр ненаполненных стеклообразных аморфных полимерных материалов связана с характером теплового молекулярного движения в них и в зависимости от химического состава и структуры материала, а также температуры окружающей среды контролируется либо α–релаксационным, либо β–релаксационным процессом. Хорошее соответствие расчетных и экспериментальных данных свидетельствует о возможности высокой эффективности использования механики трещин, которая была развита для хрупких и псевдохрупких материалов для оценки и прогнозирования долговечности стеклообразных полимеров, типа ПММА.

Для оценки долговечности густосетчатых полимеров, типа отвержденных эпоксидных смол, в которых докритический рост трещин лимитируется медленными релаксационными процессами, эффективным является подход механики разрушения, развиваемый для вязкопластичных материалов с трещинами в условиях ползучести. Следует отметить, что подходы и методы ЛУМР, разработанные применительно к гомогенным изотропным квазиупругим материалам, в частности, блочным стеклообразным полимерам, применимы также к гетерогенным анизотропным материалам типа армированных волокнами слоистых ПКМ на основе квазиупругих полимерных матриц и КС жестких листовых материалов, или субстратов (металлов и сплавов, ПКМ и т. п. ), полученных с помощью квазиупругих полимерных клеев, если макроскопический дефект (трещина) расположен и распространяется самоподобно в межслоевой плоскости (в матрице, в клеевой прослойке или в межфазной области). Клеевые композиции Большинство экспериментальных исследований трещиностойкости жестких КС проведено с использованием листов алюминиевых сплавов и эпоксидных отверждающихся клеев. Определение влияния толщины клеевой прослойки на параметры трещиностойкости КС (GIC и KIC) показало, что такое влияние практически отсутствует в случае жестких клеев, но заметно проявляется в случае эпоксидно-каучуковых (дисперсно-эластифицированных) клеев при толщине слоя до 1 мм]. Влияние толщины клеевого слоя (ширины трещины) «b» при этом аналогично блочным полимерам и связано с переходом от плосконапряженного к плоскодеформированному состоянию материала вблизи вершины трещины.

Экспериментальные данные показывают, что с повышением эластичности клеевой прослойки значения GIC возрастают, причем эти значения при нагружении по типу I значительно меньше, чем по типу II. Очень резкое деградирующее влияние на GIC оказывает воздействие воды. Поскольку в полимерных КС прорастание трещины в клеевом слое или межфазной области связано с протеканием тех же микромеханических процессов вблизи вершины трещины, что и в блочных полимерах (упругий разрыв связей и образование полос сдвига или крейз), то зависимости типа критического распространения трещины (стабильное или нестабильное псевдохрупкое или вязко-упругое) и критических параметров ТС КС от типа и условий нагружения, температуры и других факторов окружающей среды аналогичны таким зависимостям для блочных образцов при близкой природе полимеров. Исследования кинетики докритического роста в жестких полимерных КС, так же как в блочных стеклообразных полимерах, немногочисленны. В литературе найдены только две кинетические диаграммы (K-V диаграмма для длительных циклических нагрузок, см. рисунок 1, и G-V диаграмма для длительных статических нагрузок, см. рисунок 2 КС Al-эпоксидный клей. Эти данные принципиально не отличаются от результатов исследований блочных эпоксидных полимеров и очень ограничены как объектами исследований, так и условиями нагружения. Таким образом, литературные данные показывают, что подходы и методы ЛУМР применимы и очень эффективны при оценке макро- и микромеханических процессов, протекающих при росте трещин в критических и докритических длительных условиях нагружения, и при получении кинетических данных, необходимых для оценки и прогнозирования долговечности полимерных материалов и клеевых соединений в различных условиях эксплуатации (нагрузках и средах).

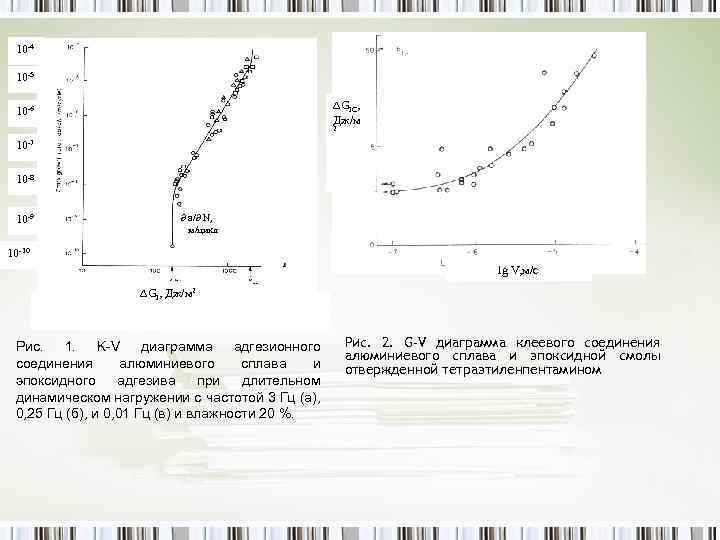10 -4 10 -5 GIС, Дж/м 10 -6 2 10 -7 10 -8 10 -9 a/ N, м/цикл 10 -10 lg V, м/с GI, Дж/м 2 Рис. 1. K-V диаграмма адгезионного соединения алюминиевого сплава и эпоксидного адгезива при длительном динамическом нагружении с частотой 3 Гц (а), 0, 25 Гц (б), и 0, 01 Гц (в) и влажности 20 %. Рис. 2. G-V диаграмма клеевого соединения алюминиевого сплава и эпоксидной смолы отвержденной тетраэтиленпентамином

Методика и пример расчета долговечности полимерных клеевых соединений с заданной трещиной в клеевом слое с использованием экспериментально полученных G – V диаграмм Имея экспериментально определенную зависимость Vдокр от GI или КI и зная величину характерного (внутренне присущего) материалу дефекта можно рассчитать зависимость статической долговечности материала от величины действующих напряжений, учитывая выражение (*) Тогда, выразив из уравнения «а» как где и учитывая, что получим подставив «а» и V в выражение (*) Где: А, n – константы, определенные по экспериментально полученной G – V диаграмме.

Пример расчета: Для образца с геометрическими размерами: в = 20 мм; h = 5 мм; с модулем упругости склеиваемых субстратов Е = 72 ГПа и при нагрузке 670 н (67 кгс), что составляет 13, 7; 14, 5 и 12, 3% от значения GIC (критического) для клеев К-300; ВК-9 и ЭПК -1, соответственно, и выбранной длине трещины а 0 = 40 мм для клеевых соединений, экспонированных в космических условиях и образцов аналогов, получим времена до разрушения соответствующие 2, 84 Е+08 с, т. е. около 9 лет. Тест 11. Вопросов 55

Спасибо за внимание