Лекция 33 Прогнозирование долговечности с учетом переменных условий

Лекция 33. Прогнозирование долговечности с учетом переменных условий эксплуатации В основе данного метода лежит принцип суперпозиций или аддитивного суммирования изменения свойств материала в различных условиях. При этом предполагается, что поскольку старение и разрушение происходит необратимо, то изменение свойств материала накапливается во времени аддитивно. Если материала находится в начале в условиях х1, а затем переносится в условия х2, то предполагается, что при этом изменение какого-либо свойства равно ∆у1, ∆у2 … ∆уn. Если в результате изменения этих свойств Δу уровень свойств становится укр, то материал становится непригодным к использованию. Принцип суперпозиций предполагает существование функции повреждаемости материала ω(у), которая является однозначной функцией свойств материала и изменение ее в разных условиях можно суммировать. Кроме того, аддитивное сложение предполагает, что сумма изменений не зависит от порядка их воздействия на материал, т. е. : Данное выражение описывает дискретное изменение свойств. Для непрерывного изменения свойств, что наблюдается на практике, выражение принимает следующий вид:

Скорость изменения какого-либо свойства у1, определяющего эксплуатационную пригодность материала, выражается следующей формулой: (****) Где: φ(х) – функция, учитывающая условия эксплуатации; f(у) – функция, описывающая состояние материала в данный момент времени и учитывающая изменение его свойств. Эта функции связаны с функцией повреждаемости: Следовательно, если материал эксплуатируется в постоянных во времени условиях, т. е. φ(х) не является функцией времени и его свойство «у1» за время жизни τ0 изменяется от у0 до укр, то из уравнения (****) можно получить следующее выражение: Где: τ0(х) – долговечность зависимости от условий х1. Если это выражение подставить в выражение (****), то получим: материала в

Проинтегрировав это выражение, получим: Где: τ – срок службы материала в переменных условиях эксплуатации; τ0(х) – срок службы материала в стационарных условиях (время достижения допустимого значения y). Чтобы выяснить физический смысл последнего равенства запишем его в дискретном виде : Где: ∆tх – время эксплуатации материала в условиях х; τ0(х) – долговечность материала в тех же условиях; - «парциальная» долговечность в условиях х (доля старения материала в этих условиях). Парциальная долговечность – доля того, на сколько материал состарился при данных условиях хранения. Сочетание этого уравнения с уравнением Аррениуса приводит к принципу температурно-временной аналогии, который устанавливает эквивалентность влияния температуры и продолжительности воздействия. Например, если при механическом воздействии, когда используется уравнение Журкова, то долговечность материала в общем виде можно рассчитать из следующего выражения: (*****)

Следствием принципа температурно-временной аналогии является существование постоянных условий эксплуатации, которые эквивалентны суммарному эффекту в переменных условиях, т. е. можно подобрать такую постоянную температуру, при которой старение материала будет точно таким же, как при переменных температурах, изменяющихся по конкретному графику. Например, в условиях механической деформации время испытания τккв при заданных условиях σ(0), Т(0) определяется соотношением: Где: σо, Т 0 – выбранные условия, которые соответствуют эксплуатации при переменных условиях σ(tx) и Т(tx). Из выражения (*****) можно вывести выражение для эквивалентной (равнодействующей) температуры, при которой свойство материала за время τэкв изменяется также как ω при переменной температуре Т(tx): Это выражение справедливо только в том случае, если температурная зависимость скорости φ(x) подчиняется уравнению Аррениуса. Это уравнение можно использовать только тогда, когда в ходе эксплуатации температура является единственным переменным фактором, который определят изменение свойств материала.

Неэмпирическое прогнозирование основано на использовании теоретических моделей, описывающих физические и химические процессы, происходящие в полимерах. При данном подходе вначале была приведена кинетическая схема радикально-цепной реакции, состоящая из 4 основных реакций: Ø 1 -я реакция: инициирование кинетической цепи путем разрыва напряженных связей макромолекул. Константа скорости этой реакции k 1 и n – число атомов в основной цепи. Ø 2–я реакция: деполимеризация радикала Rn путем отрыва мономера с константой скорости k 2. Ø 3 -я реакция: передача цепи с образованием срединного радикала и последующим распадом его с константой скорости k 3. Ø 4 -я реакция: обрыв кинетической цепи с константой скорости k 4. Подобный подход, рассматривающий механодеструкцию, имел место ранее, но при этом не учитывалось изменение механического напряжения (его увеличение) при изменении молекулярной массы (уменьшении молекулярной массы), а также изменение концентрации макромолекул во времени.

Система кинетических уравнений, записанная в соответствии с выбранной схемой реакций, позволяет учесть влияние скорости реакции на стадиях инициирования и передачи цепи на механические напряжения в связях между атомами (f), т. е. оно связывает изменение химического состава с напряжением связей между атомами в молекулах. Предполагается, что энергия активации указанных связей линейно зависит от f: Где: Еoi – энергия активации соответствующей стадии реакции в отсутствии механического поля; α΄i – структурочувствительный коэффициент, различающийся для каждой стадии. Например, для первой стадии i= 1; для второй стадии i = 3. Переходя от f к σ можно переписать выражение в следующем виде: где Где: П – характеризует степень накопления повреждений; nk – число атомов концевых участков основной цепи (на них нагрузка не действует); n 0 – максимальное число атомов основной цепи; Рn(0), Рn(t) – начальная и текущая концентрация макромолекул. Фактически П равно отношению концентрации разорванных связей в момент времени t к начальной концентрации несущих связей

Таким образом, предполагается, что распределение напряжений одинаково по всем несущим связям (носит вид ступеньки), причем связи среднего участка молекулы общим числом – (n+1– 2 nk) имеют напряжение f, а связи концевых участков являются ненагруженными, т. е. f равна нулю. Система уравнений, базирующаяся на вышеприведенных допущениях, была приведена к безразмерному виду путем введения безразмерного (условного) времени – τ. Где: t – размерное время; k 1 – константа скорости реакции для соответствующей стадии. Далее были введены безразмерные величины: Концентрации макромолекул: Где: - концентрация мономера в момент t; - концентрация мономера в начале старения Концентрации радикалов – Rп(τ): Безразмерные константы скорости деполимеризации: - деполимеризация - передача цепи - обрыв цепи

Введен параметр, характеризующий интенсивность воздействия механического поля на энергию активации инициирования: Где: α 1 – структурочувствительный коэффициент инициирования, σ – напряжение. μ показывает насколько снижает внешняя механическая нагрузка энергию активации разрушения химических связей. Параметр безразмерного соотношения структурно-чувствительных коэффициентов: значение α соответствующей реакции. Была получена система уравнений (не приводится). При решении ее упростили, предполагая, что происходит механодеструкция монодисперсного полимера при условия Для решения системы уравнений использовали метод “медленных комбинаций”. Решение уравнений позволило получить следующие зависимости: 1. 2. 3. , радикалов от безразмерного времени , мономера от безразмерного времени, - количество накопления повреждений в зависимости от безразмерного времени, 4. Получено безразмерное время разрушения – τр, 5. Изменения во времени среднечисловой молекулярной массы –

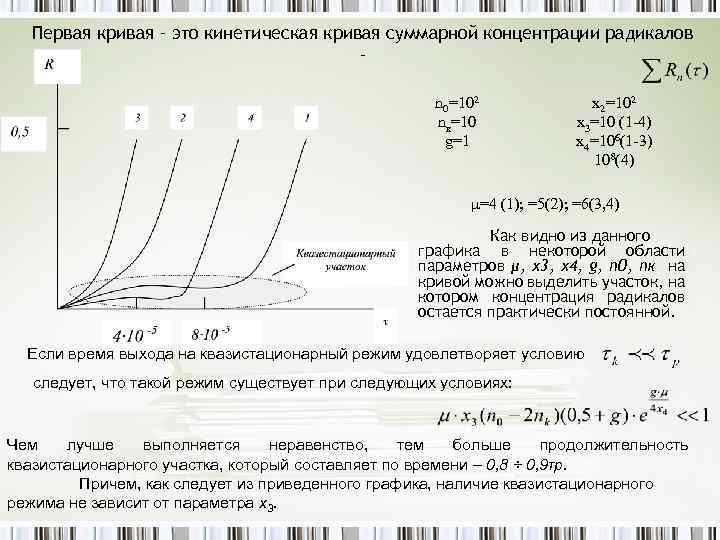Первая кривая – это кинетическая кривая суммарной концентрации радикалов – n 0=102 nк=10 g=1 х2=102 х3=10 (1 -4) х4=106(1 -3) 108(4) μ=4 (1); =5(2); =6(3, 4) Как видно из данного графика в некоторой области параметров μ, х3, х4, g, п 0, пк на кривой можно выделить участок, на котором концентрация радикалов остается практически постоянной. Если время выхода на квазистационарный режим удовлетворяет условию следует, что такой режим существует при следующих условиях: Чем лучше выполняется неравенство, тем больше продолжительность квазистационарного участка, который составляет по времени – 0, 8 ÷ 0, 9τр. Причем, как следует из приведенного графика, наличие квазистационарного режима не зависит от параметра х3.

Переход к кривым концентрации радикалов без квазистационарного участка по мере увеличения μ (кривая 3), происходит достаточно резко, что связано с наличием в уравнении экспоненциального члена, т. е. величина квазистационарной концентрации радикалов Rk определяется, главным образом, значением параметров μ и х4. Полученные при расчете кривые хорошо согласуются с наблюдаемыми закономерностями накопления радикалов в реальных полимерах при механодеструкции. Последний участок на графике, на котором происходит резкое увеличение концентрации радикалов и который составляет по времени 0, 1τр, может быть экспериментально обнаружен только в том случае когда объемное разрушение не переходит в локализованное.

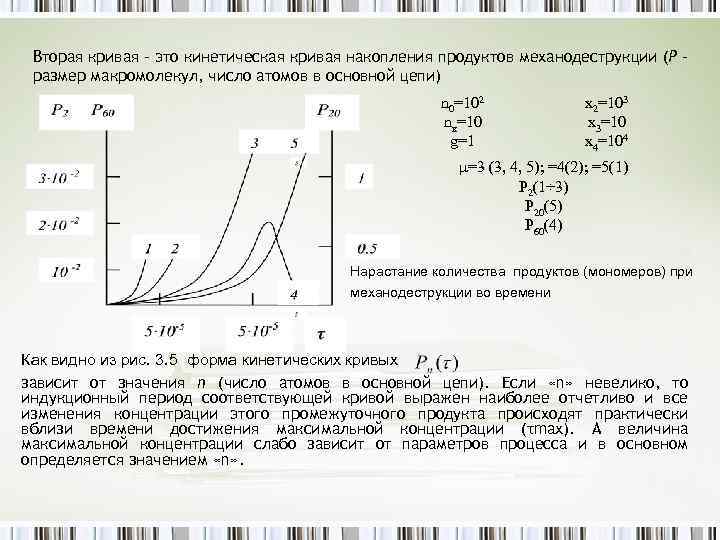Вторая кривая – это кинетическая кривая накопления продуктов механодеструкции (Р – размер макромолекул, число атомов в основной цепи) n 0=102 nк=10 g=1 х2=103 х3=10 х4=104 μ=3 (3, 4, 5); =4(2); =5(1) Р 2(1÷ 3) Р 20(5) Р 60(4) Нарастание количества продуктов (мономеров) при механодеструкции во времени Как видно из рис. 3. 5 форма кинетических кривых зависит от значения п (число атомов в основной цепи). Если «n» невелико, то индукционный период соответствующей кривой выражен наиболее отчетливо и все изменения концентрации этого промежуточного продукта происходят практически вблизи времени достижения максимальной концентрации (τmax). А величина максимальной концентрации слабо зависит от параметров процесса и в основном определяется значением «n» .

Общий анализ при различных значениях переменных показателей показывает. что скорость образования мономера в ходе механодеструкции при х≠ 0 постоянно возрастает, выход мономера – Р 2(τр) снижается по мере роста параметров μ, g и х3, а также снижения х2. В частности, снижение х2 на порядок приводит к такому уменьшению значения Р 2(τр), от параметра х4 и nк величина Р 2(τр) практически не зависит. Из экспериментальных данных известно, что обнаружение мономера при механодеструкции полистирола, проводимой при комнатной температуре, обусловлено выделением растворенного в полимере мономера. Это вполне согласуется со сделанными выше допущениями о независимости энергии активации деполимеризации (Е 2) от напряжения, поскольку равновесие: как правило, при комнатной температуре смещено в сторону образования Rn.

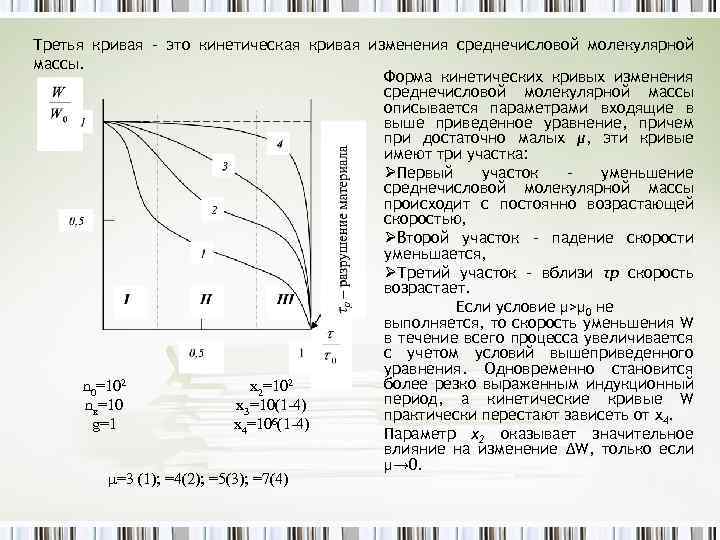Третья кривая – это кинетическая кривая изменения среднечисловой молекулярной массы. Форма кинетических кривых изменения среднечисловой молекулярной массы описывается параметрами входящие в выше приведенное уравнение, причем при достаточно малых μ, эти кривые имеют три участка: ØПервый участок – уменьшение среднечисловой молекулярной массы происходит с постоянно возрастающей скоростью, ØВторой участок – падение скорости уменьшается, ØТретий участок – вблизи τр скорость возрастает. Если условие μ>μ 0 не выполняется, то скорость уменьшения W в течение всего процесса увеличивается с учетом условий вышеприведенного уравнения. Одновременно становится 2 2 более резко выраженным индукционный n 0=10 х2=10 период, а кинетические кривые W nк=10 х3=10(1 -4) практически перестают зависеть от x 4. g=1 х4=106(1 -4) Параметр x 2 оказывает значительное влияние на изменение ΔW, только если μ→ 0. μ=3 (1); =4(2); =5(3); =7(4)

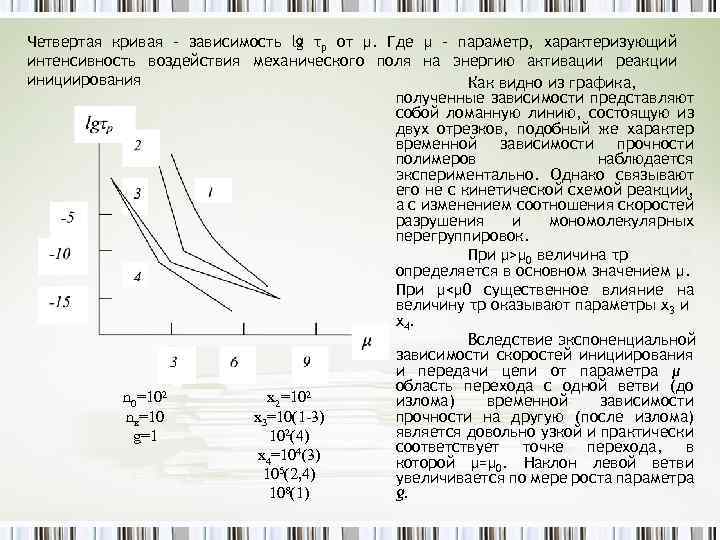Четвертая кривая – зависимость lg τр от μ. Где μ – параметр, характеризующий интенсивность воздействия механического поля на энергию активации реакции инициирования Как видно из графика, полученные зависимости представляют собой ломанную линию, состоящую из двух отрезков, подобный же характер временной зависимости прочности полимеров наблюдается экспериментально. Однако связывают его не с кинетической схемой реакции, а с изменением соотношения скоростей разрушения и мономолекулярных перегруппировок. При μ>μ 0 величина τр определяется в основном значением µ. При μ<μ 0 существенное влияние на величину τр оказывают параметры x 3 и x 4. Вследствие экспоненциальной зависимости скоростей инициирования и передачи цепи от параметра μ область перехода с одной ветви (до n 0=102 х2=102 излома) временной зависимости прочности на другую (после излома) nк=10 х3=10(1 -3) является довольно узкой и практически g=1 102(4) соответствует точке перехода, в х4=104(3) которой μ=μ 0. Наклон левой ветви 105(2, 4) увеличивается по мере роста параметра 8(1) g. 10

Если привести полученные результаты в размерный вид, то зависимость долговечности tp от напряжения в области малых σ, которые соответствуют μ<μ 0 описывается уравнением. Это выражение можно использовать для оценки долговечности твердого тела. Сопоставляя это уравнение с эмпирическим уравнением Журкова для долговечности твердых тел, можно сделать вывод, что: Где: k 01, k 03, k 04 – предэкспоненциальные члены стадии инициирования, передачи и образования цепи при термической деструкции. Таким образом, при механической деструкции полимеров предэкспоненциальный множитель t 0 в уравнении долговечности Журкова в соответствии с разработанной моделью не является средним периодом тепловых колебаний атомов, а определяется соотношением предэкспоненциальных членов элементарных стадий химических реакций термодеструкции.

Строго говоря энергия активации разрушения U 0 не совпадает с энергией активации термодеструкции Eтерм, определяемой по уменьшению веса полимера или количеству выделившегося мономера. Тогда для больших молекул, длина которых превосходит длину кинетической цепи (деполимеризации), можно записать выражение: Неэмпирическое прогнозирование, которое описано выше, является наиболее интересным и перспективным методом, который может позволить рассчитать время долговечности материала. Однако эта задача резко усложняется, если не известны химические реакции, протекающие в процессе старения материалов или не известен их химический состав. Поэтому, в настоящее время, наиболее предпочтительным является метод полуэмпирического прогнозирования, при этом необходимо, чтобы максимальное число параметров входящих в уравнение, описывающих кинетику изменения свойств имело физический смысл. Иногда при прогнозировании используются комбинированные методы, основанные на сопоставлении результатов ускоренных испытаний материалов и полученных в реальных условиях эксплуатации. В этом случае учитываются все факторы воздействующие на материал, что позволяет делать прогноз более точно. Однако в реальных условиях, когда материал принимает форму конкретного изделия, имеет определенные размеры, реализуется конкретный технологический процесс изготовления изделия, все это может влиять на его структуру и состав, и, соответственно, повлиять на долговечность, что необходимо учитывать при прогнозировании. Тест 10. Вопросов 25

Лекция 34. Прогноз долговечности полимерных материалов и клеевых соединений с использованием подходов кинетической теории долговечности и линейной механики трещин Кинетическая теория долговечности В процессе изучения закономерностей разрушения твердых тел было установлено влияние временного фактора на разрушающие напряжения. При этом были поставлены эксперименты по определению временной зависимости прочности при одноосном растяжении, которые проводили при разных температурах и напряжениях до разрушения образцов. Типичные кривые представлены на рис. Как видно из графиков с увеличением действующей нагрузки (σ) долговечность τ снижается. 1. Подходы к оценке долговечности с использованием уравнения Журкова (Гриффита). Зависимость долговечности от температуры и напряжения называется временной зависимостью прочности и описывается уравнением Журкова. Основным критерием применимости этого уравнения является линейный характер зависимостей долговечности полимера от напряжения в широком диапазоне действующих нагрузок. В настоящее время для многих полимеров проведены исследования временных зависимостей прочности в диапазоне τ около 10 порядков (от 10 -3 до 107 с). Зависимость долговечности полимеров от приложенного напряжения

Полученные экспериментальные зависимости между τ, σ и Т позволили установить аналитическое соотношение между этими величинами: Где: τ – долговечность при нагрузке σ; τо – предэкспоненциальный множитель, совпадающий с периодом тепловых колебаний атомов в твердом теле (10 -13 с); R – универсальная газовая постоянная (константа Больцмана); - энергия активации процесса разрушения; Uo – начальная энергия активации (при ненагруженном состоянии), т. е. энергия активации процесса разрушения (для полимеров Uo близка к энергии активации деструкции, т. е. к энергии разрыва межатомных связей в цепных молекулах); γ – константа материала, характеризующая локальное напряжение, (структурно чувствительный коэффициент, м 3/кмоль. Физический смысл величины γ заключается в том, что она определяет активационный объем Va, в котором осуществляется элементарный акт разрушения. где β - коэффициент перенапряжений. Если бы полимерные тела обладали идеальным строением, коэффициент γ был бы приблизительно одинаковым для всех тел и равным ~10 -23 см 3 (объем атома). Такие тела должны были бы обладать теоретической прочностью. В действительности коэффициент γ значительно больше, чем 10 -23 см 3, и составляет (40 -150) 10 -23 см 3, что связано с наличием локальных перенапряжений в области дефектов (микротрещин), всегда существующих в реальных полимерных телах. При ориентации или термической обработке полимеров величина γ уменьшается, а долговечность возрастает.

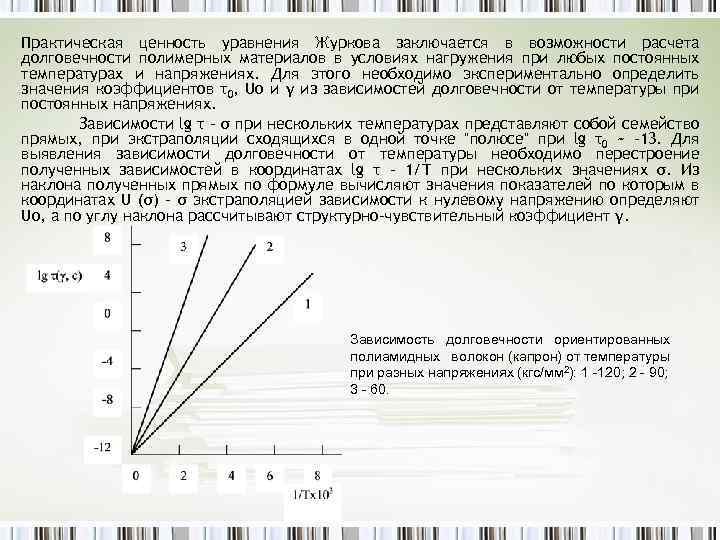Практическая ценность уравнения Журкова заключается в возможности расчета долговечности полимерных материалов в условиях нагружения при любых постоянных температурах и напряжениях. Для этого необходимо экспериментально определить значения коэффициентов τ0, Uo и γ из зависимостей долговечности от температуры при постоянных напряжениях. Зависимости lg τ - σ при нескольких температурах представляют собой семейство прямых, при экстраполяции сходящихся в одной точке "полюсе" при lg τ0 ~ -13. Для выявления зависимости долговечности от температуры необходимо перестроение полученных зависимостей в координатах lg τ - 1/Т при нескольких значениях σ. Из наклона полученных прямых по формуле вычисляют значения показателей по которым в координатах U (σ) - σ экстраполяцией зависимости к нулевому напряжению определяют Uo, а по углу наклона рассчитывают структурно-чувствительный коэффициент γ. Зависимость долговечности ориентированных полиамидных волокон (капрон) от температуры при разных напряжениях (кгс/мм 2): 1 -120; 2 - 90; 3 - 60.

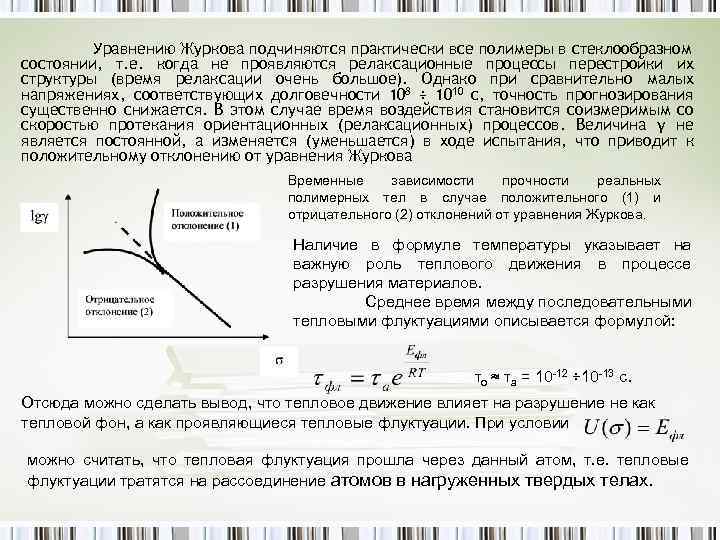Уравнению Журкова подчиняются практически все полимеры в стеклообразном состоянии, т. е. когда не проявляются релаксационные процессы перестройки их структуры (время релаксации очень большое). Однако при сравнительно малых напряжениях, соответствующих долговечности 108 ÷ 1010 с, точность прогнозирования существенно снижается. В этом случае время воздействия становится соизмеримым со скоростью протекания ориентационных (релаксационных) процессов. Величина γ не является постоянной, а изменяется (уменьшается) в ходе испытания, что приводит к положительному отклонению от уравнения Журкова Временные зависимости прочности реальных полимерных тел в случае положительного (1) и отрицательного (2) отклонений от уравнения Журкова. Наличие в формуле температуры указывает на важную роль теплового движения в процессе разрушения материалов. Среднее время между последовательными тепловыми флуктуациями описывается формулой: τо ≈ τа = 10 -12 ÷ 10 -13 c. Отсюда можно сделать вывод, что тепловое движение влияет на разрушение не как тепловой фон, а как проявляющиеся тепловые флуктуации. При условии можно считать, что тепловая флуктуация прошла через данный атом, т. е. тепловые флуктуации тратятся на рассоединение атомов в нагруженных твердых телах.

Приложенная к телу растягивающая нагрузка уменьшает энергию распада связи, т. е. приложении внешней нагрузки механические разрывы между атомами будут наблюдаться чаще, чем без нее. Кроме того, облегчив термофлуктуационный распад связей, внешняя нагрузка затрудняет их рекомбинацию поскольку атомы оказываются отодвинутыми друг от друга на большие расстояния, чем только при термофлуктуации. В этом случае для воссоединения атомов необходима тепловая флуктуация больше, чем обычно, что реализуется не всегда. В результате тепловых флуктуаций распад связей происходит чаще, чем их воссоединение. Таким образом, внешняя сила «усиливает» , облегчает и направляет разрушающее действие флуктуаций. В высокоэластическом состоянии, когда скорость релаксационных процессов резко возрастает, временная зависимость прочности полимеров не подчиняется уравнению Журкова, для нее справедлив степенной закон долговечности: Где: m - постоянная, характеризующая материал; где С - константа. Поскольку реальные тела обладают гетерогенным строением на надатомном уровне, внешняя действующая сила распределяется неравномерно между связями. В результате возникают локальные напряжения, причем в этих местах энергия активации распада межатомных связей снижается особенно сильно. Именно здесь формируются очаги разрушения, развитие которых ведет к разрушению тела в целом.

2. Оценка долговечности с использованием подходов линейной механики трещин. Первый постулат – во всех материалах имеются дефекты (повреждения). В процессе развития (эволюции) повреждения локализуются (сливаются, или агрегируют и взаимодействуют друг с другом), поскольку напряжения вокруг них возрастают с их ростом, что увеличивает интенсивность протекающих при этом процессов. При этом возникает и наиболее интенсивно растет один наибольший дефект (магистральная трещина или макроскопическая зона неупругих деформаций), либо образуются кластеры повреждений (разветвленные дефекты). При критических условиях нагружения эти процессы протекают очень быстро, и параметрами прочности служат нагрузки, вызывающие их. При нагрузках, существенно меньших критических, для описания кинетики докритического развития дефектов используют эмпирические уравнения. Для описания скорости роста магистральной трещины при статических и циклических нагрузках эти уравнения имеют вид Где: а – длина магистральной трещины; t, N – длительность статического и число циклов динамического нагружения соответственно; G, ΔG – статическая нагрузка и амплитудное значение циклической нагрузки на трещину соответственно; А, В, n, m – эмпирические константы. В случае агрегирования дефектов скорость роста характерного размера кластеров (корреляционной длины, или радиуса корреляции ) описывается скейлинговыми соотношениями: Где: C, D, df - эмпирические константы (фрактальная размерность кластеров).

Определение времени или числа циклов, необходимых для прорастания длины магистральной трещины от начальной (ао) до критической (ас) или радиуса корреляции кластера от 0 до с, позволяет определять статическую или динамическую (усталостную) долговечность соответственно: Поведение вязкоупругих тел Материал называется вязкоупругим, если в нем при любой нагрузки наряду с мгновенными упругими деформациями наблюдается неупругие, величина которых зависит от длительности и скорости приложения нагрузки. При этом в зависимости от того является ли зависимости между напряжением и скоростью деформирования линейной или нелинейной различают: линейные и нелинейные вязкоупругие материалы. 1. Вязкоупругий материал считают идеально нелинейноупругим, если приложении механической нагрузки в нем развивается только обратимые деформации: Ø Мгновенные упругие (Гуковские); Ø Вязкоупругие, зависящие от времени (эластические). Причем если деформирование такого материала происходит под действием постоянного напряжения, то обратимая вязкоупругая составляющая деформации стремиться во времени к некоторому предельному равновесному значению (модель Кельвина-Фойхта).

2. В идеальном линейно-вязкоупругом материале под действием приложенного напряжения, наряду с обратимыми деформациями развиваются также необратимые деформации идеального ньютоновского течения, которые при действии постоянной нагрузки неограниченно возрастают во времени (модель Максвелла). 3. В нелинейном вязкоупругом материале деформации течения являются неньютоновским. 1. Линейно вязкоупругие тела: В механике трещин показано, что в отличие от линейно упругих и псевдоупругих материалов, разрушение линейно вязкоупругих материалов с трещинами при их нагружении в режиме ползучести может происходить при нагрузке, меньше критической, даже в отсутствии воздействия окружающей среды. При этом постулируется (устанавливается), что в таких условиях разрушение линейно вязкоупругих материалов происходит идеально хрупко, без докритического подрастания трещин, а критическое (быстрое) прорастание трещин наступает спустя некоторое время (tp) после мгновенного приложения постоянной нагрузки. Время задержки разрушения (tp) для таких материалов является временем, которое необходимо для снижения критического напряжения, соответствующего данной длине трещины, за счет уменьшения модуля упругости при ползучести. Это является эквивалентным снижению сопротивления вязко-упругого материала к росту трещин с увеличением длительности действия статической нагрузки. Для линейных вязко-упругих материалов коэффициент интенсивности напряжения К(t) определяется не только значениями внешней нагрузки, которая действует в настоящий момент времени, но и всеми ее значениями за все время пребывания материала с трещиной в напряженном состоянии, т. е. всей историей его нагружения.

Считают, что время до разрушения (tp) линейновязкоупругих материалов с трещинами, которые нагружается в режиме ползучести может быть определено в общем виде из следующего выражения: Где: Еf – линейный временной оператор, П(t-S) – ядро ползучести (область, в которой развивается деформация), характеризует память материала и зависит от его реологических характеристик, t – Текущее время, S – Прошедший момент времени, р(t-S) – ядро релаксации. 2. Вязкоупругие тела Для вязкоупругих материалов (модель Максвелла) время tp определяется следующем образом: Где: σ(0) – критическое напряжение по Гриффиту (Журкову), σ(t) – постоянно приложенное напряжение, τр – время релаксации.

Из этого выражения следует, что вязкоупругие тела с трещинами при нагружении в режиме ползучести разрушается через какое-то время при любых, даже сколь угодно малых нагрузках. Для таких материалов – нет значения Gп. Время до разрушения таких материалов при статическом нагружении легко оценить по формуле: Причем коэффициент интенсивности тем меньше, чем меньше τр – время релаксации. Таким образом, долговечность вязкоупругих материалов Максвеловского типа при заданном уровне статической нагрузки определяется единственным параметром – это время релаксации. Вязкоупругое поведение многих реальных материалов, в том числе стеклообразных термопластов, хорошо описывается уравнением наследственной теории упругости, которое позволяет рассчитать значение tp. (*) Где: w, α, β, х – параметры характеризующие реологические свойства материала, Е 0 , Е∞ – мгновенный и установившийся модуль упругости, τр– время релаксации.

Из уравнения (*) следует, что время до разрушения при статическом нагружении реальных вязкоупругих материалов с трещинами в решающей степени как и для идеальных материалов Максвеловского типа определяется их реологическими характеристиками и, прежде всего, времени релаксации, Однако в отличии от идеальных материалов Максвелловского типа, для реальных вязкоупругих материалов существует такое значение напряжения, ниже которого критическое состояние не наступает как угодно долго, т. е. существует безопасное (пороговое) значение напряжений σδ(σП), которое определяется из этой формулы при t→∞. С увеличением времени релаксации линейно-вязкоупругого материала (τР→∞) безопасное напряжение увеличивается, стремясь в пределе к критическому напряжению линейно-упругого материала с трещиной, т. е. к критическому напряжению по Гриффиту σ0. Следовательно, линейно-вязкоупругие материалы с большими временами релаксации по своему поведению аналогичны линейноупругим материалам Их критическое напряжение по Гриффиту можно рассматривать как безопасное напряжение, ниже которого разрушение не происходит, даже при очень длительном воздействии статической нагрузки, а при σ > σ0 разрушении происходит практически мгновенно со скоростью примерно равной скорости звука.

Спасибо за внимание