МОР_03.ppt
- Количество слайдов: 20
 Лекция № 3 Симплекс-метод решение задачи с начальным базисом
Лекция № 3 Симплекс-метод решение задачи с начальным базисом
 Условие задачи Предприятие производит продукцию двух видов (А и Б), используя при изготовлении этой продукции ресурсы трех видов (пер вого, второго и третьего). Чтобы произвести одну единицу продукции А, нужно затратить 2 единицы первого и 1 единицу второго ресурса. Для производства единицы продукции В требуется 1 единица первого ресурса, 3 единицы второго и 1 единица третьего ресурсов. Запасы ресурсов у предприятия ограничены: на складах есть 64 единиц первого ресурса, 72 единицы второго и 20 единиц третьего ресурсов. Рыночная цена единицы продукции А составляет 4 руб. , а цена продукции В равна 6 руб. Сколько продукции следует произвести, чтобы получить наибольшую выручку?
Условие задачи Предприятие производит продукцию двух видов (А и Б), используя при изготовлении этой продукции ресурсы трех видов (пер вого, второго и третьего). Чтобы произвести одну единицу продукции А, нужно затратить 2 единицы первого и 1 единицу второго ресурса. Для производства единицы продукции В требуется 1 единица первого ресурса, 3 единицы второго и 1 единица третьего ресурсов. Запасы ресурсов у предприятия ограничены: на складах есть 64 единиц первого ресурса, 72 единицы второго и 20 единиц третьего ресурсов. Рыночная цена единицы продукции А составляет 4 руб. , а цена продукции В равна 6 руб. Сколько продукции следует произвести, чтобы получить наибольшую выручку?
 Условие задачи Пусть предприятие планирует произвести х1 единиц про дукции А и х2 единиц продукции В, тогда выручка предприятия Z будет, очевидно, равна Z = 4 х1 +6 Х 2. Величины х1 и х2 по условию применения симплекс метода должны быть неотрицательными, а общие расходы ресурсов при производстве продукции не должны превысить запасы этих ресурсов.
Условие задачи Пусть предприятие планирует произвести х1 единиц про дукции А и х2 единиц продукции В, тогда выручка предприятия Z будет, очевидно, равна Z = 4 х1 +6 Х 2. Величины х1 и х2 по условию применения симплекс метода должны быть неотрицательными, а общие расходы ресурсов при производстве продукции не должны превысить запасы этих ресурсов.
 Условие задачи Требуется найти такой план производства, чтобы его выполнение обеспечивало предприятию наибольшую выручку, т. е. Z = 4 х1 +6 Х 2 → MAX при выполнении ограничений: х1 ≥ 0, х2 ≥ 0.
Условие задачи Требуется найти такой план производства, чтобы его выполнение обеспечивало предприятию наибольшую выручку, т. е. Z = 4 х1 +6 Х 2 → MAX при выполнении ограничений: х1 ≥ 0, х2 ≥ 0.
 Решение задачи Вначале запишем условие задачи в канонической форме. , то есть ограничения неравенства перепишем в виде равенств, добавляя балансовые переменные : где: Эта система является системой с базисом (базис это величины , каждая из которых входит только в одно уравнение системы с коэффициентом равным единице, х1 и х2 свободные переменные.
Решение задачи Вначале запишем условие задачи в канонической форме. , то есть ограничения неравенства перепишем в виде равенств, добавляя балансовые переменные : где: Эта система является системой с базисом (базис это величины , каждая из которых входит только в одно уравнение системы с коэффициентом равным единице, х1 и х2 свободные переменные.
 Решение задачи Задачи, при решении которых применяется симплекс метод, должны обладать следующими двумя свойствами: система ограничений должна быть системой с базисом; свободные члены всех уравнений в системе должны быть неотрицательны. Полученная нами система – система с базисом и ее свободные члены неотрицательны, следовательно, можно применить симплекс метод. Составим первую симплекс таблицу (Итерация 0), то есть таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных.
Решение задачи Задачи, при решении которых применяется симплекс метод, должны обладать следующими двумя свойствами: система ограничений должна быть системой с базисом; свободные члены всех уравнений в системе должны быть неотрицательны. Полученная нами система – система с базисом и ее свободные члены неотрицательны, следовательно, можно применить симплекс метод. Составим первую симплекс таблицу (Итерация 0), то есть таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных.
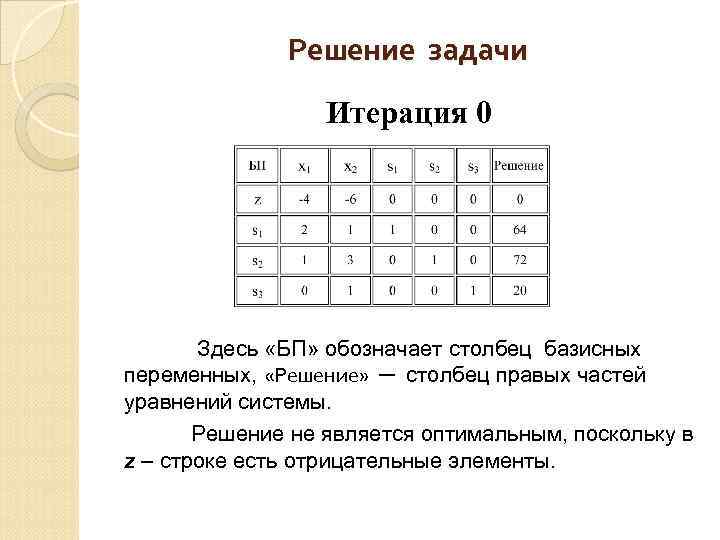 Решение задачи Итерация 0 Здесь «БП» обозначает столбец базисных переменных, «Решение» ─ столбец правых частей уравнений системы. Решение не является оптимальным, поскольку в z – строке есть отрицательные элементы.
Решение задачи Итерация 0 Здесь «БП» обозначает столбец базисных переменных, «Решение» ─ столбец правых частей уравнений системы. Решение не является оптимальным, поскольку в z – строке есть отрицательные элементы.
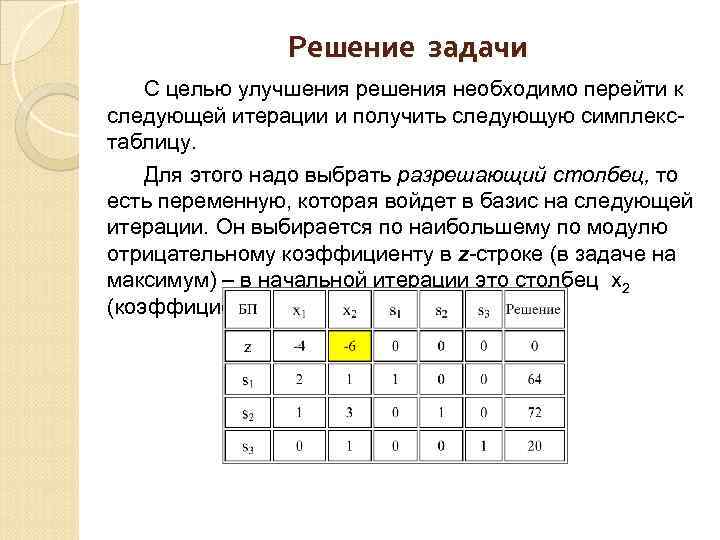 Решение задачи С целью улучшения решения необходимо перейти к следующей итерации и получить следующую симплекс таблицу. Для этого надо выбрать разрешающий столбец, то есть переменную, которая войдет в базис на следующей итерации. Он выбирается по наибольшему по модулю отрицательному коэффициенту в z строке (в задаче на максимум) – в начальной итерации это столбец x 2 (коэффициент равен – 6).
Решение задачи С целью улучшения решения необходимо перейти к следующей итерации и получить следующую симплекс таблицу. Для этого надо выбрать разрешающий столбец, то есть переменную, которая войдет в базис на следующей итерации. Он выбирается по наибольшему по модулю отрицательному коэффициенту в z строке (в задаче на максимум) – в начальной итерации это столбец x 2 (коэффициент равен – 6).
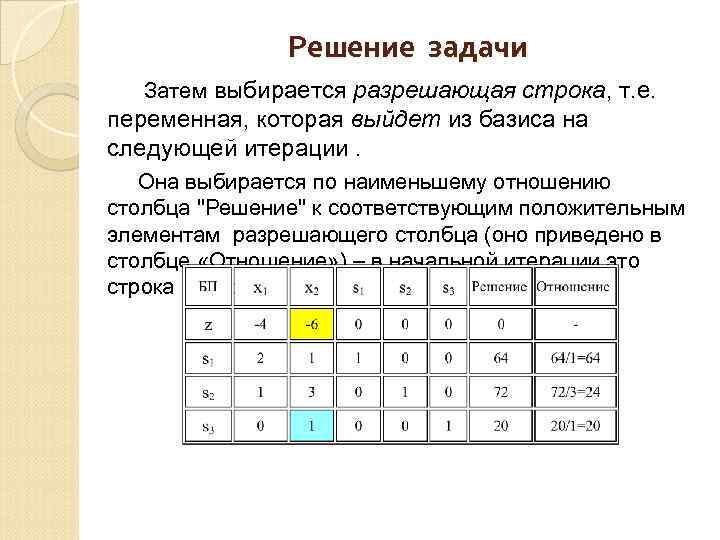 Решение задачи Затем выбирается разрешающая строка, т. е. переменная, которая выйдет из базиса на следующей итерации. Она выбирается по наименьшему отношению столбца "Решение" к соответствующим положительным элементам разрешающего столбца (оно приведено в столбце «Отношение» ) – в начальной итерации это строка s 3 ( для нее отношение 20).
Решение задачи Затем выбирается разрешающая строка, т. е. переменная, которая выйдет из базиса на следующей итерации. Она выбирается по наименьшему отношению столбца "Решение" к соответствующим положительным элементам разрешающего столбца (оно приведено в столбце «Отношение» ) – в начальной итерации это строка s 3 ( для нее отношение 20).
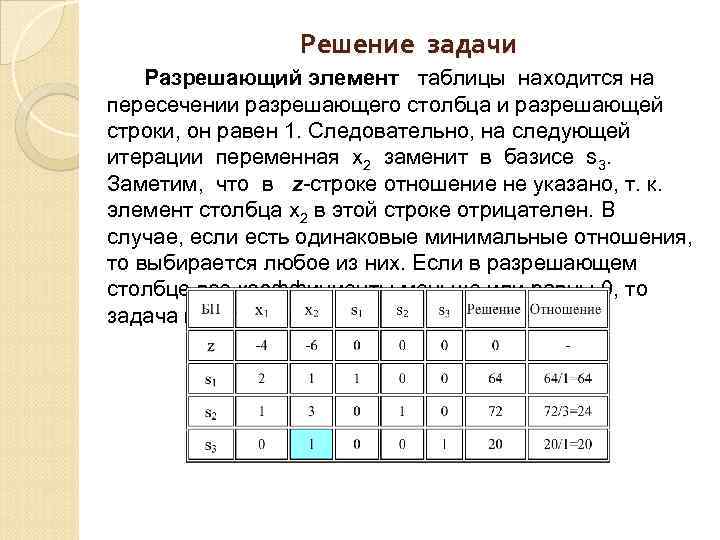 Решение задачи Разрешающий элемент таблицы находится на пересечении разрешающего столбца и разрешающей строки, он равен 1. Следовательно, на следующей итерации переменная x 2 заменит в базисе s 3. Заметим, что в z строке отношение не указано, т. к. элемент столбца x 2 в этой строке отрицателен. В случае, если есть одинаковые минимальные отношения, то выбирается любое из них. Если в разрешающем столбце все коэффициенты меньше или равны 0, то задача имеет бесконечное множество решений.
Решение задачи Разрешающий элемент таблицы находится на пересечении разрешающего столбца и разрешающей строки, он равен 1. Следовательно, на следующей итерации переменная x 2 заменит в базисе s 3. Заметим, что в z строке отношение не указано, т. к. элемент столбца x 2 в этой строке отрицателен. В случае, если есть одинаковые минимальные отношения, то выбирается любое из них. Если в разрешающем столбце все коэффициенты меньше или равны 0, то задача имеет бесконечное множество решений.
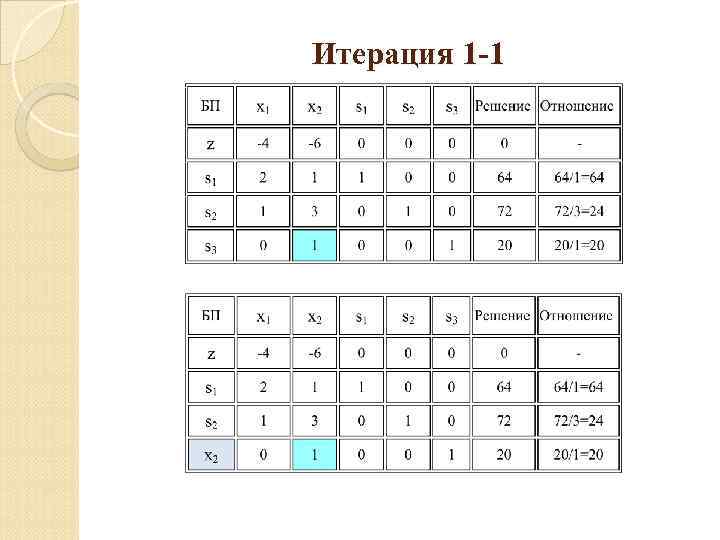
 Решение задачи Заполним следующую таблицу «Итерация 1» . Ее мы получим из таблицы «Итерация 0» . Наша цель превратить разрешающий столбец х2 в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов). 1. Вычисление строки х2 таблицы "Итерация 1". Разделив все члены разрешающей строки s 3 таблицы "Итерация 0" на разрешающий элемент, получим строку x 2 в таблице «Итерация 1» . Т. к. разрешающий элемент в данном случае равен 1, то строка s 3 таблицы "Итерация 0" будет совпадать со строкой х2 таблицы "Итерация 1 « и будет иметь вид
Решение задачи Заполним следующую таблицу «Итерация 1» . Ее мы получим из таблицы «Итерация 0» . Наша цель превратить разрешающий столбец х2 в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов). 1. Вычисление строки х2 таблицы "Итерация 1". Разделив все члены разрешающей строки s 3 таблицы "Итерация 0" на разрешающий элемент, получим строку x 2 в таблице «Итерация 1» . Т. к. разрешающий элемент в данном случае равен 1, то строка s 3 таблицы "Итерация 0" будет совпадать со строкой х2 таблицы "Итерация 1 « и будет иметь вид
 Итерация 1 -1
Итерация 1 -1
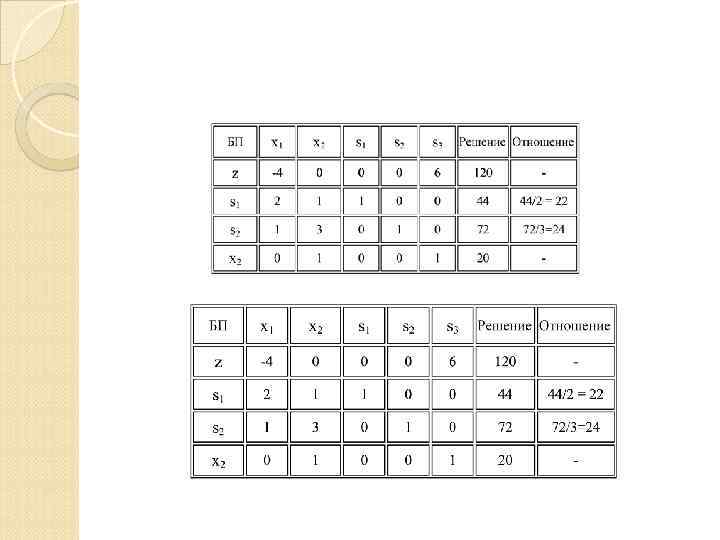
 Решение задачи Теперь найдем остальные строки таблицы «Итерация 1» . Вычисление z строки. На месте члена ( 6) должен быть 0, поэтому все элементы найденной строки х2 умножим на 6, и сложим полученную строку с z строкой таблицы «Итерация 0» . Тогда z cтрока в таблице «Итерация 1» и вся таблица будут иметь вид
Решение задачи Теперь найдем остальные строки таблицы «Итерация 1» . Вычисление z строки. На месте члена ( 6) должен быть 0, поэтому все элементы найденной строки х2 умножим на 6, и сложим полученную строку с z строкой таблицы «Итерация 0» . Тогда z cтрока в таблице «Итерация 1» и вся таблица будут иметь вид
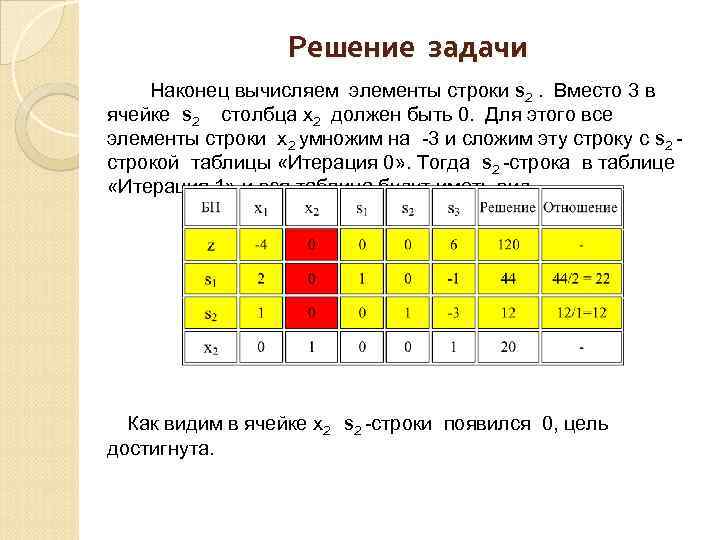
 Решение задачи Вычисляем элементы строки s 1. Вместо 1 в ячейке s 1 столбца х2 должен быть 0. Для этого все элементы строки х2 умножим на 1 и сложим полученную строку с s 1 строкой таблицы «Итерация 0» . Тогда s 1 cтрока в таблице «Итерация 1» и вся таблица будут иметь вид Как видим в ячейке х2 s 1 строки появился 0, цель достигнута.
Решение задачи Вычисляем элементы строки s 1. Вместо 1 в ячейке s 1 столбца х2 должен быть 0. Для этого все элементы строки х2 умножим на 1 и сложим полученную строку с s 1 строкой таблицы «Итерация 0» . Тогда s 1 cтрока в таблице «Итерация 1» и вся таблица будут иметь вид Как видим в ячейке х2 s 1 строки появился 0, цель достигнута.
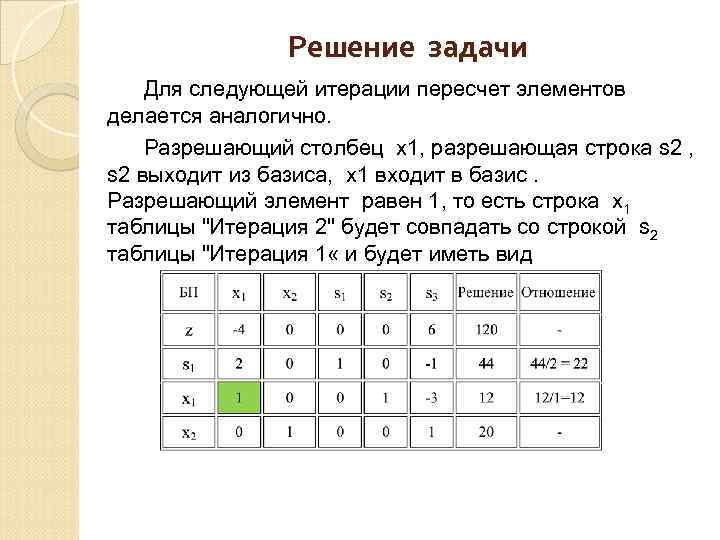
 Решение задачи Наконец вычисляем элементы строки s 2. Вместо 3 в ячейке s 2 столбца х2 должен быть 0. Для этого все элементы строки х2 умножим на 3 и сложим эту строку с s 2 строкой таблицы «Итерация 0» . Тогда s 2 cтрока в таблице «Итерация 1» и вся таблица будут иметь вид Как видим в ячейке х2 s 2 строки появился 0, цель достигнута.
Решение задачи Наконец вычисляем элементы строки s 2. Вместо 3 в ячейке s 2 столбца х2 должен быть 0. Для этого все элементы строки х2 умножим на 3 и сложим эту строку с s 2 строкой таблицы «Итерация 0» . Тогда s 2 cтрока в таблице «Итерация 1» и вся таблица будут иметь вид Как видим в ячейке х2 s 2 строки появился 0, цель достигнута.
 Решение задачи Для следующей итерации пересчет элементов делается аналогично. Разрешающий столбец х1, разрешающая строка s 2 , s 2 выходит из базиса, х1 входит в базис. Разрешающий элемент равен 1, то есть строка х1 таблицы "Итерация 2" будет совпадать со строкой s 2 таблицы "Итерация 1 « и будет иметь вид
Решение задачи Для следующей итерации пересчет элементов делается аналогично. Разрешающий столбец х1, разрешающая строка s 2 , s 2 выходит из базиса, х1 входит в базис. Разрешающий элемент равен 1, то есть строка х1 таблицы "Итерация 2" будет совпадать со строкой s 2 таблицы "Итерация 1 « и будет иметь вид
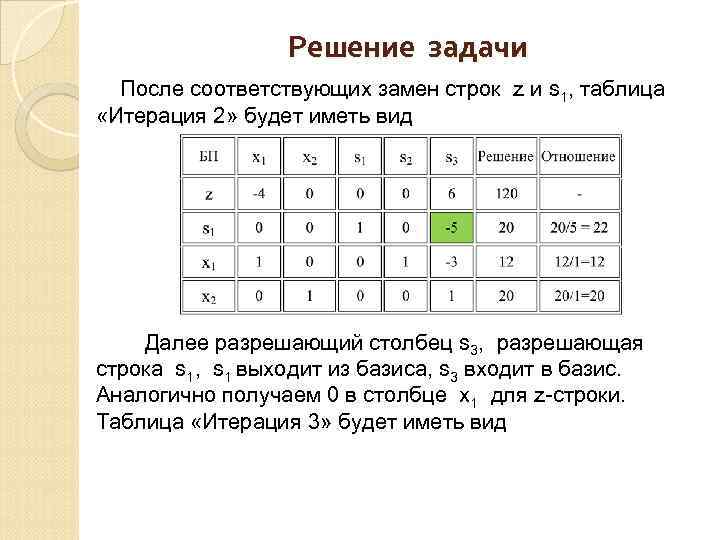 Решение задачи После соответствующих замен строк z и s 1, таблица «Итерация 2» будет иметь вид Далее разрешающий столбец s 3, разрешающая строка s 1, s 1 выходит из базиса, s 3 входит в базис. Аналогично получаем 0 в столбце х1 для z строки. Таблица «Итерация 3» будет иметь вид
Решение задачи После соответствующих замен строк z и s 1, таблица «Итерация 2» будет иметь вид Далее разрешающий столбец s 3, разрешающая строка s 1, s 1 выходит из базиса, s 3 входит в базис. Аналогично получаем 0 в столбце х1 для z строки. Таблица «Итерация 3» будет иметь вид
 Решение задачи В z строке все коэффициенты неотрицательны, следовательно, получено оптимальное решение : х1 = 24, х2 = 16, zmax = 192.
Решение задачи В z строке все коэффициенты неотрицательны, следовательно, получено оптимальное решение : х1 = 24, х2 = 16, zmax = 192.
 СПАСИБО ЗА ВНИМАНИЕ!
СПАСИБО ЗА ВНИМАНИЕ!


