 Лекция № 3 Процессы на входе дисперсии в фильтр и процессы на выходе дисперсии из фильтра
Лекция № 3 Процессы на входе дисперсии в фильтр и процессы на выходе дисперсии из фильтра
 Явления переноса в процессах фильтрования: • В зависимости от области применения процессы ультра- и микро- фильтрации (УФ- и МФ) характеризуются широким спектром разделяемых смесей от истинных растворов до дисперсных систем, включая эмульсии и суспензии, и применяемых мембран, размеры пор которых изменяются в широком диапазоне от нанометров до микрометров. Поэтому при анализе процессов переноса компонентов разделяемой смеси используют ряд моделей, выбор которых зависит от специфики объектов разделения и структуры мембран, а также от интуиции исследователя. • Для иллюстрации принципа выбора соответствующих моделей механизма массового переноса в процессах УФ и МФ, рассмотрим их как процессы фазового взаимодействия по аналогии с традиционными массообменными процессами, допуская, что в процессах УФ и МФ температура ретанта и пермеата одинакова.
Явления переноса в процессах фильтрования: • В зависимости от области применения процессы ультра- и микро- фильтрации (УФ- и МФ) характеризуются широким спектром разделяемых смесей от истинных растворов до дисперсных систем, включая эмульсии и суспензии, и применяемых мембран, размеры пор которых изменяются в широком диапазоне от нанометров до микрометров. Поэтому при анализе процессов переноса компонентов разделяемой смеси используют ряд моделей, выбор которых зависит от специфики объектов разделения и структуры мембран, а также от интуиции исследователя. • Для иллюстрации принципа выбора соответствующих моделей механизма массового переноса в процессах УФ и МФ, рассмотрим их как процессы фазового взаимодействия по аналогии с традиционными массообменными процессами, допуская, что в процессах УФ и МФ температура ретанта и пермеата одинакова.
 Движущая сила процессов фильтрования Обобщенные потоки - растворенного вещества и -растворителя представим в виде: Где L- кинетические коэффициенты; ∆μ- движущие силы, рассмотренные как разности электрохимических потенциалов; 1 и 2 нижние индекс характеризующие растворенное вещество и растворитель. Электрохимический потенциал ∆μi i-го компонента любой из фаз запишем в виде: а разность потенциалов i-го компонента в фазах J и K соответственно: Где PVа- давление парциальный полный объем и активности; ∆μ 0 i - стандартный химический потенциал i-ого компонента. Если рассмотрим в близи поверхности мембраны элементарный объем, в нем можно выделить еще ряд фаз: (Z) Фаза 1 -Истинный раствор. Фаза 2 -гель. Фаза 3 -Связанный слой. Фаза 4 -матрица мембраны (фильтра). В связанном слое при изотермических условиях давление:
Движущая сила процессов фильтрования Обобщенные потоки - растворенного вещества и -растворителя представим в виде: Где L- кинетические коэффициенты; ∆μ- движущие силы, рассмотренные как разности электрохимических потенциалов; 1 и 2 нижние индекс характеризующие растворенное вещество и растворитель. Электрохимический потенциал ∆μi i-го компонента любой из фаз запишем в виде: а разность потенциалов i-го компонента в фазах J и K соответственно: Где PVа- давление парциальный полный объем и активности; ∆μ 0 i - стандартный химический потенциал i-ого компонента. Если рассмотрим в близи поверхности мембраны элементарный объем, в нем можно выделить еще ряд фаз: (Z) Фаза 1 -Истинный раствор. Фаза 2 -гель. Фаза 3 -Связанный слой. Фаза 4 -матрица мембраны (фильтра). В связанном слое при изотермических условиях давление:
 Двухпараметрическая модель селективной адсорбции: Согласно данной модели на поверхности мембраны преимущественные адсорбируется один компонентов раствора. Под действием давления сорбированный компонент переносится через поры мембраны и собирается на противоположенной ее поверхности в виде пермеата.
Двухпараметрическая модель селективной адсорбции: Согласно данной модели на поверхности мембраны преимущественные адсорбируется один компонентов раствора. Под действием давления сорбированный компонент переносится через поры мембраны и собирается на противоположенной ее поверхности в виде пермеата.
 Модель можно формализовать двумя этапами: • 1 -й этап сорбция на межфазной поверхности «мембрана-раствор» обусловлена комплексом взаимодействия в системе «растворенное вещество- растворитель мембрана» . Эти взаимодействия включают электростатические, молекулярные, полярные и др. Общим результатом взаимодействий является равновесные условия, определяющие предпочтительную адсорбцию на мембране одного из компонента. • 2 -ой этап кинетический связан с движением растворителя и растворенного вещества через пору. На скорость их переноса в порах при градиенте давления оказывают влияние как термодинамические условия, так и силы трения и сдвига, определяющие в совокупности разделяющую способности мембран. При установившихся условиях осуществляется одновременно движение растворителя и растворенного вещества через поры мембраны и накопление у поверхности мембраны вещества (КП), Которое переносится за счет диффузии в объем ретанта.
Модель можно формализовать двумя этапами: • 1 -й этап сорбция на межфазной поверхности «мембрана-раствор» обусловлена комплексом взаимодействия в системе «растворенное вещество- растворитель мембрана» . Эти взаимодействия включают электростатические, молекулярные, полярные и др. Общим результатом взаимодействий является равновесные условия, определяющие предпочтительную адсорбцию на мембране одного из компонента. • 2 -ой этап кинетический связан с движением растворителя и растворенного вещества через пору. На скорость их переноса в порах при градиенте давления оказывают влияние как термодинамические условия, так и силы трения и сдвига, определяющие в совокупности разделяющую способности мембран. При установившихся условиях осуществляется одновременно движение растворителя и растворенного вещества через поры мембраны и накопление у поверхности мембраны вещества (КП), Которое переносится за счет диффузии в объем ретанта.
 Капиллярно-фильтрационная модель селективной проницаемости: Согласно данной модели, на поверхности и внутри пор гидрофильной мембраны образуется «связанный» слой толщина которого δ, гидратированный ион переносится через мембрану при условии dгидр< dпор+2δ в противном случае мембрана его задерживает. Вмести с тем, не следует думать, что задерживающая способность мембраны в данной модели обусловлена лишь соотношением размеров. В первую очередь задерживающая способность зависит от конкурентной борьбы иона и мембраны за связанную воду. Анализ адекватности данной модели реальному процессу привел к развитию методов определения размеров пор различных типов мембран.
Капиллярно-фильтрационная модель селективной проницаемости: Согласно данной модели, на поверхности и внутри пор гидрофильной мембраны образуется «связанный» слой толщина которого δ, гидратированный ион переносится через мембрану при условии dгидр< dпор+2δ в противном случае мембрана его задерживает. Вмести с тем, не следует думать, что задерживающая способность мембраны в данной модели обусловлена лишь соотношением размеров. В первую очередь задерживающая способность зависит от конкурентной борьбы иона и мембраны за связанную воду. Анализ адекватности данной модели реальному процессу привел к развитию методов определения размеров пор различных типов мембран.
 Селективность ультрафильтрационных и микрофильтрационных мембран как функция порометрического распределения: Согласно данной модели, все потоки проходить через поры, которые составляют определенную долю поверхности мембраны и имеют характерное распределение по размерам. Движущей силой потока растворителя является градиент давления. Модель отличается физической простотой и очевидной умозрительной привлекательностью. Она широко используется при описании УФ и МФ. Считают, что эффективность задерживания растворного вещества такой мембраной зависит от соотношений размеров гидратированных молекул и размеров гидратированных пор мембраны. Допускают, что поры цилиндрические и перпендикулярны поверхности мембраны. Такому допущению отвечают разработанные в лаборатории ядерных реакции объединенного института ядерных реакций под руководством академика Г. Н. Флерова мембраны ядерные фильтры. Поток воды проходящий через поры, определяют по уравнению Пуазейля: Где J’ [M 3/M 2 C]-производительность мембраны по воде, N- общее число пор на единицу поверхности мембраны [1/М 2], r-средний радиус пор [m], ∆Р- [Н/М 2] перепад давления на мембране, μ- динамический коэффициент вязкости [Па. с], L [m]- толщина мембраны.
Селективность ультрафильтрационных и микрофильтрационных мембран как функция порометрического распределения: Согласно данной модели, все потоки проходить через поры, которые составляют определенную долю поверхности мембраны и имеют характерное распределение по размерам. Движущей силой потока растворителя является градиент давления. Модель отличается физической простотой и очевидной умозрительной привлекательностью. Она широко используется при описании УФ и МФ. Считают, что эффективность задерживания растворного вещества такой мембраной зависит от соотношений размеров гидратированных молекул и размеров гидратированных пор мембраны. Допускают, что поры цилиндрические и перпендикулярны поверхности мембраны. Такому допущению отвечают разработанные в лаборатории ядерных реакции объединенного института ядерных реакций под руководством академика Г. Н. Флерова мембраны ядерные фильтры. Поток воды проходящий через поры, определяют по уравнению Пуазейля: Где J’ [M 3/M 2 C]-производительность мембраны по воде, N- общее число пор на единицу поверхности мембраны [1/М 2], r-средний радиус пор [m], ∆Р- [Н/М 2] перепад давления на мембране, μ- динамический коэффициент вязкости [Па. с], L [m]- толщина мембраны.
 Так как общая площадь пор то Радиус молекул растворенного вещества обычно рассчитывают по уравнению Эйнштейна-Стокса: Где-К=1, 38*10 -23 [Дж/К]- константа Больцмана. Радиусы пор мембраны определяются различными методами: По водопроницаемости, Гидродинамическими, Обработкой микрофотографии, По электросопротивлению, и др. Для оценки эффективности задерживающей способности мембран вводят понятия: наблюдаемая селективность R и истинная селективность Ru: Где С и Х – Мольные доли и объемные массовые концентрации растворенного вещества в растворе.
Так как общая площадь пор то Радиус молекул растворенного вещества обычно рассчитывают по уравнению Эйнштейна-Стокса: Где-К=1, 38*10 -23 [Дж/К]- константа Больцмана. Радиусы пор мембраны определяются различными методами: По водопроницаемости, Гидродинамическими, Обработкой микрофотографии, По электросопротивлению, и др. Для оценки эффективности задерживающей способности мембран вводят понятия: наблюдаемая селективность R и истинная селективность Ru: Где С и Х – Мольные доли и объемные массовые концентрации растворенного вещества в растворе.
 Проницаемость пористой мембраны при разделении двухфазных жидких систем: На поверхности и внутри пор лиофильной мембраны, находящейся в растворе формируется слой связанной жидкости некоторой толщина Н, который образует особую фазу со своей границей раздела. В первом приближением слой связанной жидкости можно моделировать последовательным пропусканием через мембрану двух жидкостей. После пропитывания мембраны первой жидкостью под действием градиента внешнего давления начинается течение второй жидкости через поры, что показано на рис. № 1 в виде схемы иллюстрирующей взаимодействия двухфазного потока с поверхностью цилиндрического капилляра. Перемещение продавливаемой жидкости в пору сопровождается формированием капиллярного мениска, направление которого в данной системе
Проницаемость пористой мембраны при разделении двухфазных жидких систем: На поверхности и внутри пор лиофильной мембраны, находящейся в растворе формируется слой связанной жидкости некоторой толщина Н, который образует особую фазу со своей границей раздела. В первом приближением слой связанной жидкости можно моделировать последовательным пропусканием через мембрану двух жидкостей. После пропитывания мембраны первой жидкостью под действием градиента внешнего давления начинается течение второй жидкости через поры, что показано на рис. № 1 в виде схемы иллюстрирующей взаимодействия двухфазного потока с поверхностью цилиндрического капилляра. Перемещение продавливаемой жидкости в пору сопровождается формированием капиллярного мениска, направление которого в данной системе
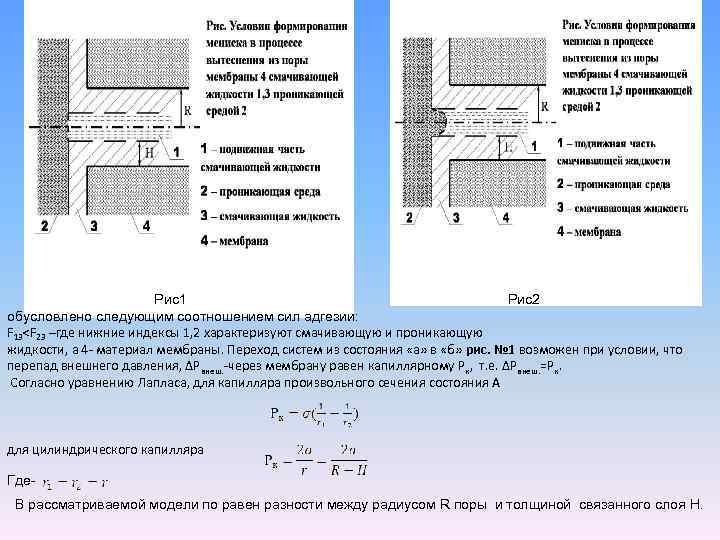 Рис1 Рис2 обусловлено следующим соотношением сил адгезии: F 13
Рис1 Рис2 обусловлено следующим соотношением сил адгезии: F 13
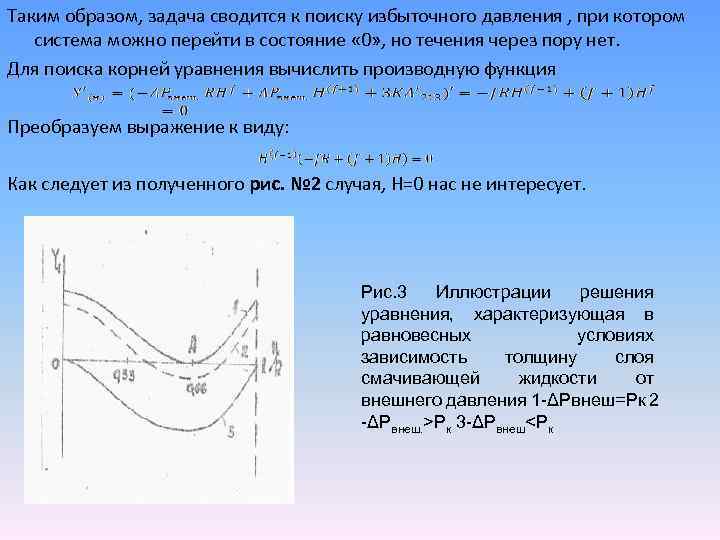 Таким образом, задача сводится к поиску избыточного давления , при котором система можно перейти в состояние « 0» , но течения через пору нет. Для поиска корней уравнения вычислить производную функция Преобразуем выражение к виду: Как следует из полученного рис. № 2 случая, Н=0 нас не интересует. Рис. 3 Иллюстрации решения уравнения, характеризующая в равновесных условиях зависимость толщину слоя смачивающей жидкости от внешнего давления 1 -ΔРвнеш=Рк 2 -ΔРвнеш. >Рк 3 -ΔРвнеш<Рк
Таким образом, задача сводится к поиску избыточного давления , при котором система можно перейти в состояние « 0» , но течения через пору нет. Для поиска корней уравнения вычислить производную функция Преобразуем выражение к виду: Как следует из полученного рис. № 2 случая, Н=0 нас не интересует. Рис. 3 Иллюстрации решения уравнения, характеризующая в равновесных условиях зависимость толщину слоя смачивающей жидкости от внешнего давления 1 -ΔРвнеш=Рк 2 -ΔРвнеш. >Рк 3 -ΔРвнеш<Рк
 Спасибо за внимание
Спасибо за внимание


