Лекция 3 Представление числовой информации в памяти компьютера

Лекция 3 Представление числовой информации в памяти компьютера

План лекции: 1. 2. 3. Представление целых в памяти ЭВМ Представление вещественных чисел в памяти ЭВМ Абсолютная и относительная погрешность при представлении вещественных чисел

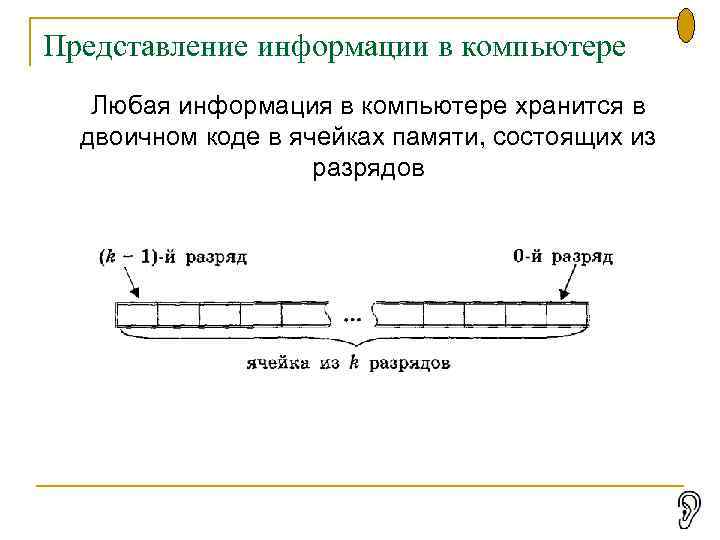Представление информации в компьютере Любая информация в компьютере хранится в двоичном коде в ячейках памяти, состоящих из разрядов

Особенности представления чисел в компьютере Представлены с помощью двоичного алфавита Хранятся в ограниченном числе разрядов (поэтому, операции с вещественными числами дают погрешность в вычислениях)

Имеются различные способы кодирования для: целых положительных (без знака) чисел; целых чисел со знаком; вещественных чисел

1. Представление целых чисел в памяти ЭВМ

Наибольшую последовательность бит, которую процессор ЭВМ может обрабатывать как единое целое, называют машинным словом. Разряды в машинном слове нумеруются справа налево, начиная с 0.

Все целые числа в компьютере хранятся в машинных словахи разделяются на - числа без знака (только положительные) - числа со знаком (положительные и отрицательные). У чисел со знаком старший разряд машинного слова отводится под знак. 0 в старшем разряде - положительное число, 1 - отрицательное

Пример 1 В восьмиразрядное машинное слово можно записать А) беззнаковые числа от 0 до 255 (28 -1 ) 0000 1111 Б) числа со знаком от 0 до 127 (27 -1 ) 0000 01111111

Диапазон целых чисел В n разрядной целочисленной компьютерной арифметике 2 n = 0 (машинный ноль)

1. 1 Целые числа без знака

Для представления в памяти целого десятичного числа без знака используется прямой код: 1. Число переводится в двоичную систему 2. Двоичную запись слева дополняют таким количеством нулей, сколько требует тип данных числа

Пример 1 Записать представление в памяти ЭВМ беззнакового числа 10 типа byte 00001010 Пример 2 Записать представление в памяти ЭВМ беззнакового числа 300 типа byte 100101100

1. 2 Целые числа со знаком

Для представления в компьютере целых чисел со знаком (положительных и отрицательных) используют дополнительный код Дополнительный код нужен для того, чтобы закодировать знак «минус» и свести процедуру вычитания к сложению

Дополнительный код целого положительного числа со знаком совпадает с его прямым кодом

Дополнительный код отрицательного числа n - разрядный дополнительный код отрицательного числа m – это запись в n разрядах положительного числа 2 n - |m|, где |m| - модуль отрицательного числа m ДК – это дополнение модуля m до 2 n (или до машинного нуля в n-разрядной арифметике)

1 й способ получения ДК отрицательного числа (по определению ДК) Пример 3: Найти дополнительный код числа -5 (integer) 1) Тип integer предполагает, что число будет хранится в 16 -ти разрядном машинном слове 2) ДК равен тому числу, которое нужно добавить модулю -5 (101) чтобы получить 16 -ти разрядный машинный ноль 10000000000000000 -101= 1111111011

2 -й способ получения ДК отрицательного числа (алгоритм без вычитания) Дополнительный код целого отрицательного числа со знаком может быть получен по следующему алгоритму: 1) записать прямой код модуля числа; 2) инвертировать его (заменить 1 на 0, 0 на 1); 3) полученный обратный код сложить с единицей

Пример 4: Записать дополнительный код числа (– 5), интерпретируя его как величину типа integer Пример 5: Записать дополнительный код числа 35000, интерпретируя его как величину типа integer 100010111000

Пример: вычитание сводится к сложению в дополнительном коде 10 -5=5 0000001010 1111111011 -------------10000000101

Перевод числа из дополнительного кода в десятичную систему счисления Если число положительное, то просто перевести его код в десятичную систему счисления. Если число отрицательное необходимо выполнить следующий алгоритм: 1) вычесть из кода числа 1; 2) инвертировать код; 3) перевести в десятичную систему счисления 4) полученное число записать со знаком минус. Пример 6: Запишите в десятичной системе счисления целое число, если дан его дополнительный код 1111 1010 1101

2. Представление вещественных чисел в памяти ЭВМ

Вещественные числа (конечные и бесконечные десятичные дроби) хранятся в компьютере в формате с плавающей точкой, который опирается на нормализованную форму записи чисел

Основная проблема при представлении вещественных чисел – точность представления (хранится может лишь ограниченное количество значащих цифр)

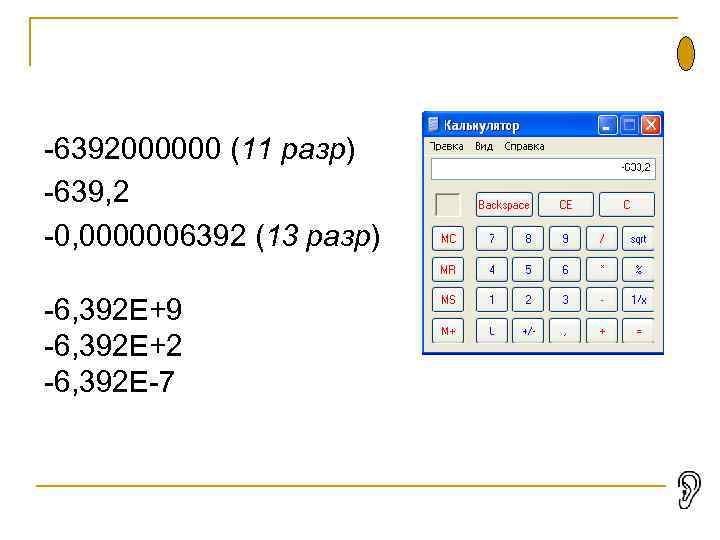-6392000000 (11 разр) -639, 2 -0, 0000006392 (13 разр) -6, 392 Е+9 -6, 392 Е+2 -6, 392 Е-7

Экспоненциальная форма числа Любое число A в экспоненциальной форме представляется в виде А = ±m*Bp, где B — основание системы счисления, m — мантисса числа, p — порядок числа.

Экспоненциальные формы числа 25, 324 -2 2532, 4*10 -3 25324*10 2, 5324*101 2 0, 25324*10

Нормализованная форма записи чисел В десятичной системе: А = М ∙ 10 p, где М – мантисса числа (1 M < 10), p — порядок числа (целое число)

Вопрос Какое представление числа 25, 324 соответствует нормализованной форме? 2532, 4*10 -2 25324*10 -3 2, 5324*101 0, 25324*102

Нормализованная форма записи чисел В двоичной системе: А = 1, М ∙ 2 p, M — мантисса (ее целая часть равна 12), p — порядок, записанный в десятичной системе счисления

Вопрос Какое представление данных чисел соответствует нормализованной форме? 11111010, 0011(2) = 0, 0110110(2) =

Хранение вещественного числа в памяти компьютера При записи нормализованного числа в компьютере хранятся значения знака числа, мантиссы и смещенного порядка

Смещение В памяти компьютера хранится не само значение порядка, а значение порядка со смещением (смещенный порядок) Порядок может быть числом со знаком + или Смещенный порядок имеет только положительное значение Смещение выбирают так, чтобы минимальному значению истинного порядка соотвествовал 0

Правила представления вещественных чисел описаны в международном стандарте IEEE 754 - стандарте двоичной арифметики с плавающей точкой

Стандарт IEEE 754 -1985 определят: как представлять нормализованные положительные и отрицательные вещественные числа как представлять нулевые числа как представлять специальную величину бесконечность (Infiniti) как представлять специальную величину "Не число" (Na. N) четыре режима округления Стандарт определяет четыре формата представления чисел с плавающей запятой: с одинарной точностью (single-precision) 32 бита с двойной точностью (double-precision) 64 бита с одинарной расширенной точностью (single-extended precision) >=43 бит (редко используемый) с двойной расширенной точностью (double-extended precision) >= 79 бит (обычно используют 80 бит)

Формат представления с одинарной точностью (Single) Занимает в памяти 32 бита. Знак – 1 разряд Смещенный порядок – 8 разрядов Мантисса - 23 разряда Смещение равно 127 (10) = 01111111 (2)

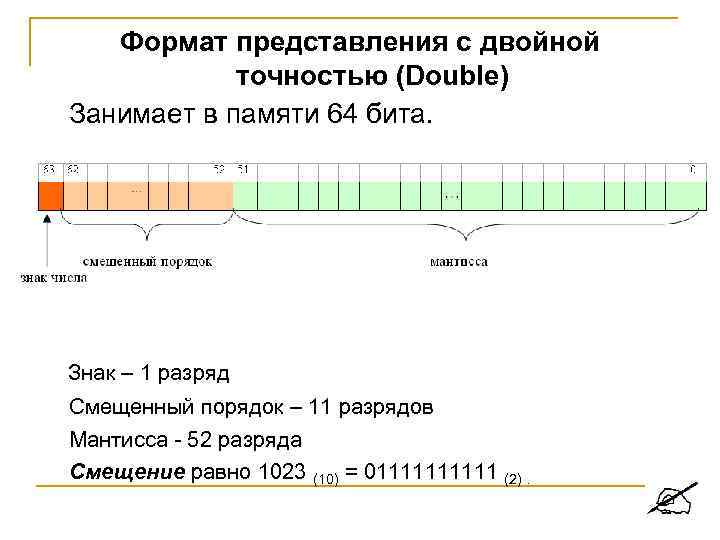Формат представления с двойной точностью (Double) Занимает в памяти 64 бита. Знак – 1 разряд Смещенный порядок – 11 разрядов Мантисса - 52 разряда Смещение равно 1023 (10) = 011111 (2).

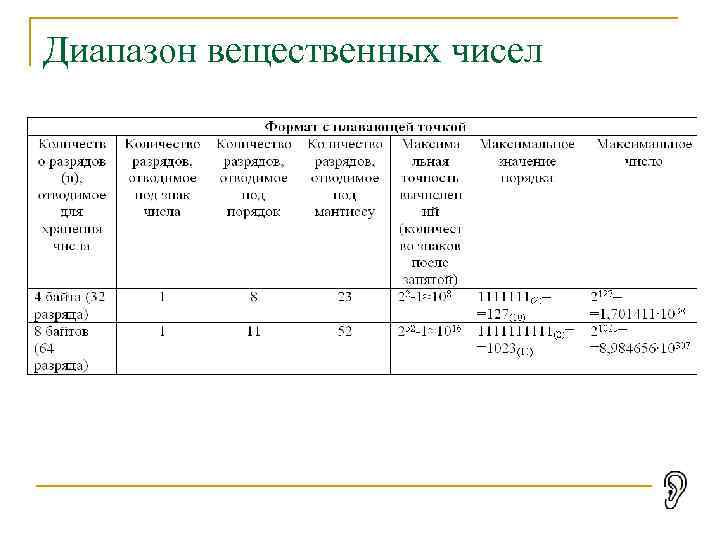Диапазон вещественных чисел

Для записи внутреннего представления вещественного числа необходимо: 1. перевести модуль данного числа в двоичную систему счисления 2. нормализовать двоичное число т. е. записать в виде 1, M * 2 p, где M — мантисса (ее целая часть равна 1(2)) и p — порядок, записанный в десятичной системе счисления 3. прибавить к порядку смещение +127(для Single) +1023 (для Double) и перевести полученное число (смещенный порядок) в двоичную систему счисления 4. учитывая знак числа, выписать его представление в 4 -х (8 ми) байтовом машинном слове (дополнив мантиссу необходимым количеством нулей справа)

Семинар

Семинар Упражнение 1: Запишите однобайтный прямой код числа без знака 12 (10) Упражнение 2: Запишите прямой код числа 21 (10), интерпретируя его как шестнадцатибитное целое без знака.

Семинар Упражнение 3: Запишите двухбайтный дополнительный код числа 12(10) Упражнение 4: Запишите дополнительный код числа -21(10), интерпретируя его как шестнадцатибитовое целое со знаком.

Семинар Упражнение 5: Записать целое десятичное число, соответствующее дополнительному коду 00000010111 Упражнение 6: Записать целое десятичное число, соответствующее дополнительному коду 11111000000

Семинар Запишите код действительного числа 155, 625 интерпретируя его как величину типа Single Запишите код действительного числа -87, 375, интерпретируя его как величину типа Double. Запишите код действительного числа 22, 25, интерпретируя его как величину типа Double. Дан код величины типа Double 408 EFB 00000. Преобразуйте его в число Дан код величины типа Double С 078 D 2800000. Преобразуйте его в число