Начерталка3.ppt
- Количество слайдов: 43

Лекция 3 • Плоскость. Способы задания плоскости. Плоскости частного положения (уровня и проецирующие) • Следы плоскости. • Принадлежность точки и прямой плоскости. • Главные линии плоскости. • Определение угла наклона плоскости к плоскостям проекций. • Взаимное расположение плоскостей. • Взаимное расположение прямой и плоскости.

Плоскость задается движением прямой образующей линии « n » по прямой направляющей линии «m» параллельно заданному направлению «S»

Плоскость задана тремя точками, не лежащими на одной прямой α α 1

Плоскость задана прямой и точкой, не лежащей на ней α α 1
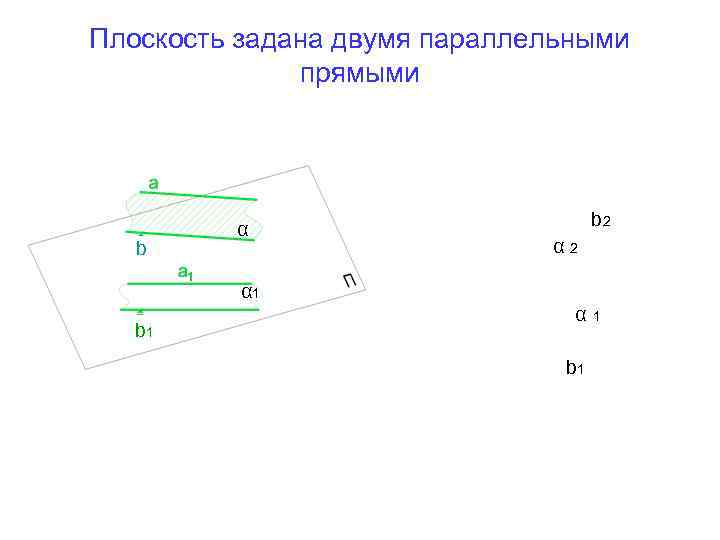
Плоскость задана двумя параллельными прямыми b α b 2 α 1 b 1
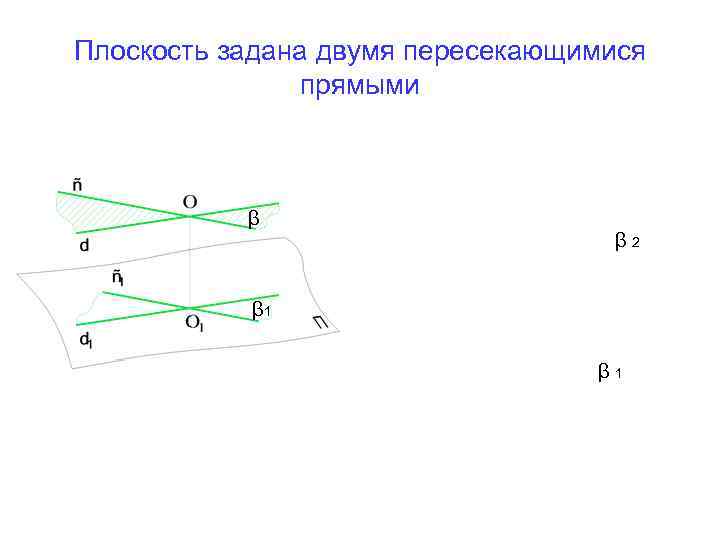
Плоскость задана двумя пересекающимися прямыми β β 2 β 1
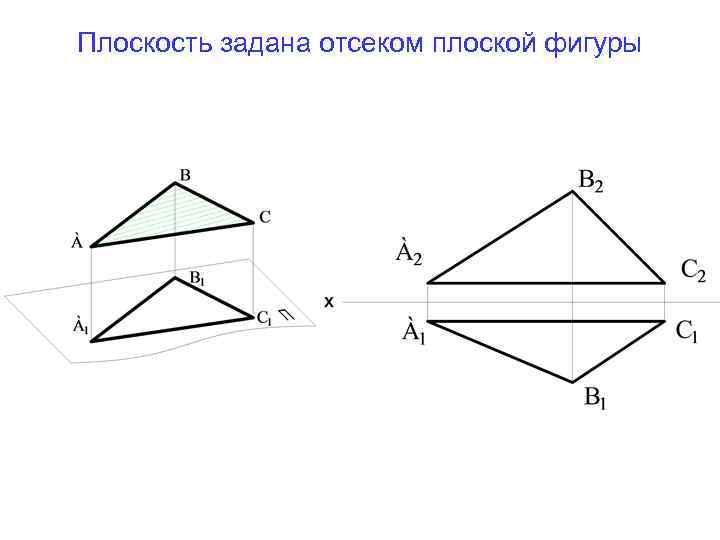
Плоскость задана отсеком плоской фигуры

Плоскость задана следами Следом плоскости называется линия пересечения данной плоскости с какой-либо плоскостью проекций Рп 1 - горизонтальный след плоскости Рп 2 - фронтальный след плоскости Рп 3 - профильный след плоскости

Следы плоскости можно построить по одноименным следам двух прямых, лежащих в этой плоскости. Например, если плоскость задана двумя пересекающимися прямыми 1 -2 и 3 -4, определяем фронтальные и горизонтальные следы этих прямых. Соответственно, фронтальный след плоскости пройдет через проекции точек 12 и 32, горизонтальный след плоскости – через горизонтальные проекции точек 41 и 21 а
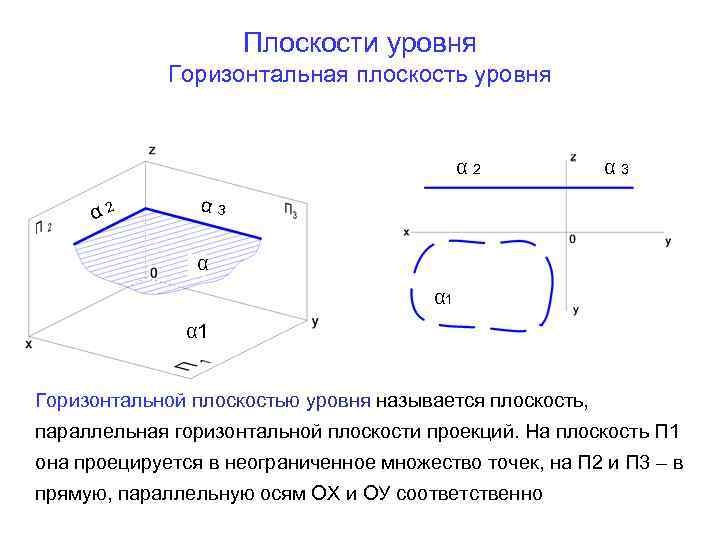
Плоскости уровня Горизонтальная плоскость уровня α 2 α 3 α α 1 Горизонтальной плоскостью уровня называется плоскость, параллельная горизонтальной плоскости проекций. На плоскость П 1 она проецируется в неограниченное множество точек, на П 2 и П 3 – в прямую, параллельную осям ОХ и ОУ соответственно

Фронтальная плоскость уровня β 3 β 2 β β 1 β 2 β 3 β 1 Фронтальной плоскостью уровня называется плоскость, параллельная фронтальной плоскости проекций. На плоскость П 2 она проецируется в неограниченное множество точек; на П 1 – в прямую, параллельную оси ОХ ; на П 3 – в прямую, перпендикулярную оси ОУ
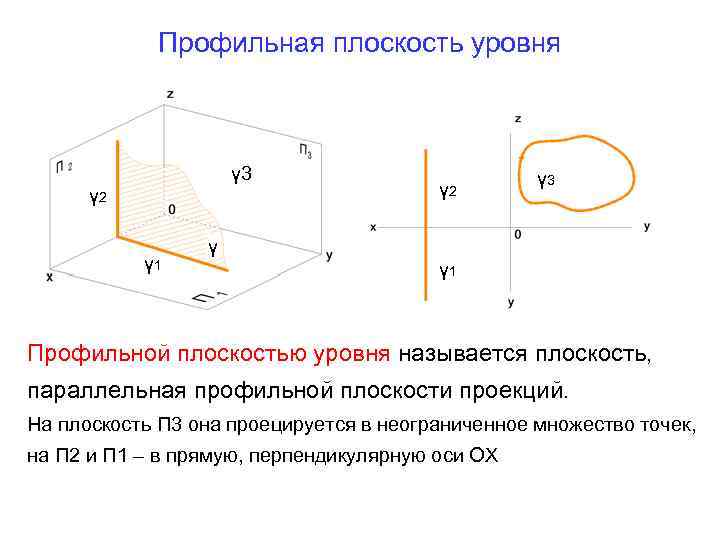
Профильная плоскость уровня γ 3 γ 2 γ 1 γ γ 2 γ 3 γ 1 Профильной плоскостью уровня называется плоскость, параллельная профильной плоскости проекций. На плоскость П 3 она проецируется в неограниченное множество точек, на П 2 и П 1 – в прямую, перпендикулярную оси ОХ
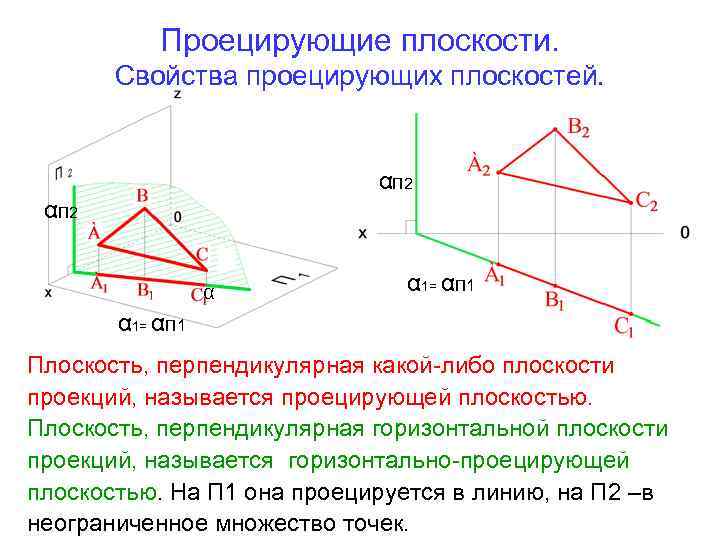
Проецирующие плоскости. Свойства проецирующих плоскостей. αП 2 α α 1= αП 1 Плоскость, перпендикулярная какой-либо плоскости проекций, называется проецирующей плоскостью. Плоскость, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей плоскостью. На П 1 она проецируется в линию, на П 2 –в неограниченное множество точек.
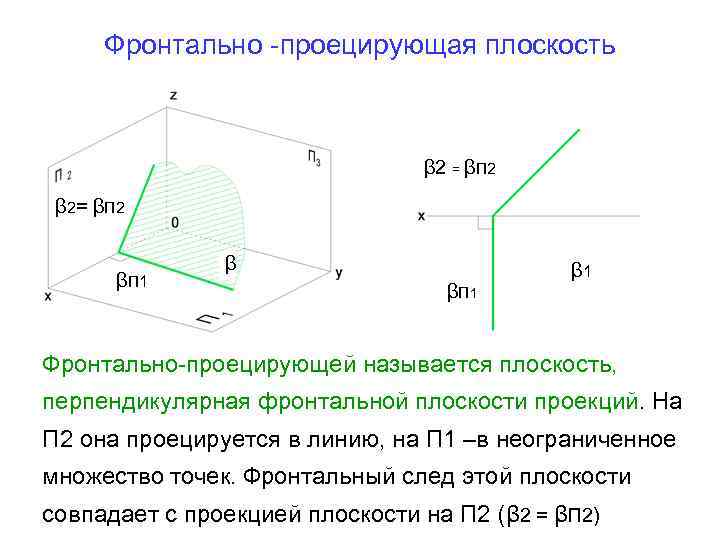
Фронтально -проецирующая плоскость β 2 = βП 2 β 2= βП 2 βП 1 β 1 Фронтально-проецирующей называется плоскость, перпендикулярная фронтальной плоскости проекций. На П 2 она проецируется в линию, на П 1 –в неограниченное множество точек. Фронтальный след этой плоскости совпадает с проекцией плоскости на П 2 (β 2 = βП 2)
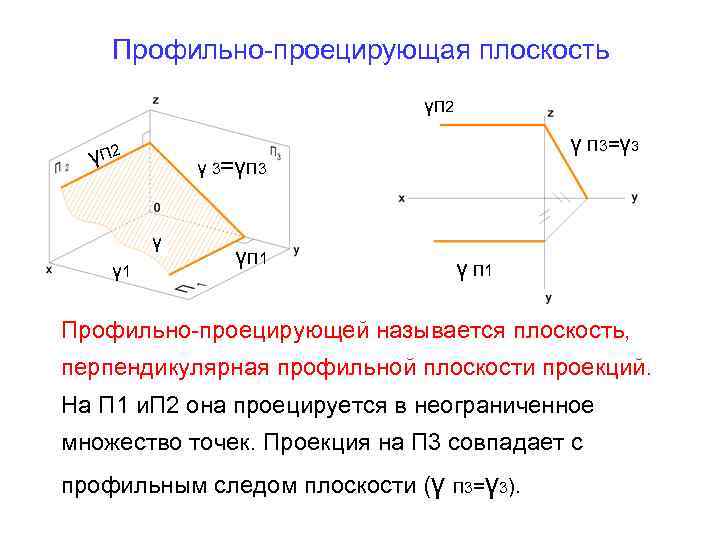
Профильно-проецирующая плоскость γП 2 γ 3=γП 3 γ γ 1 γ П 3=γ 3 γП 1 γ П 1 Профильно-проецирующей называется плоскость, перпендикулярная профильной плоскости проекций. На П 1 и. П 2 она проецируется в неограниченное множество точек. Проекция на П 3 совпадает с профильным следом плоскости (γ γ П 3= 3).

Принадлежность прямой плоскости b b 1 b 2 b 1 Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие этой плоскости.
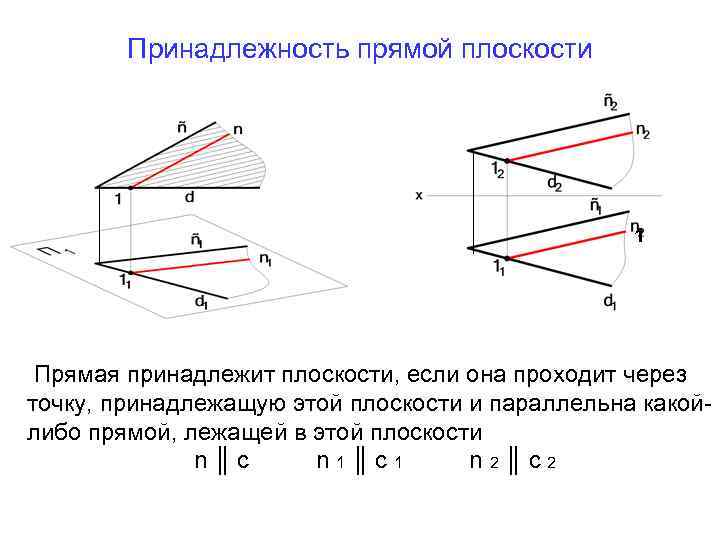
Принадлежность прямой плоскости 1 Прямая принадлежит плоскости, если она проходит через точку, принадлежащую этой плоскости и параллельна какойлибо прямой, лежащей в этой плоскости n║c n 1║c 1 n 2║c 2
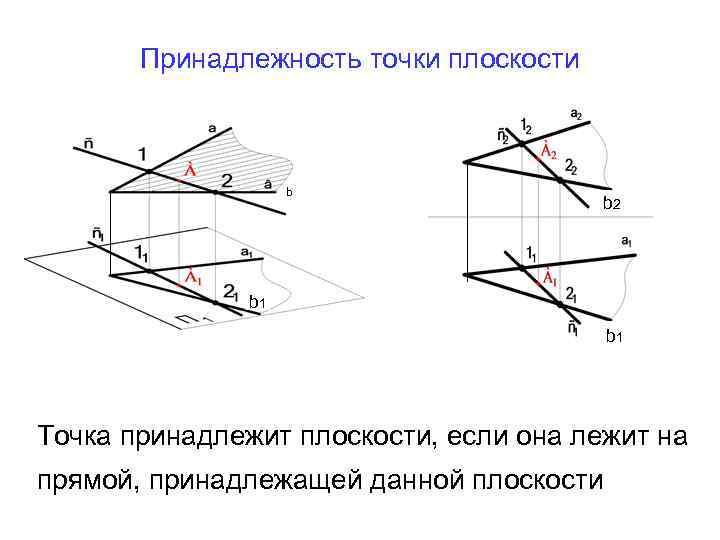
Принадлежность точки плоскости b b 2 b 1 Точка принадлежит плоскости, если она лежит на прямой, принадлежащей данной плоскости
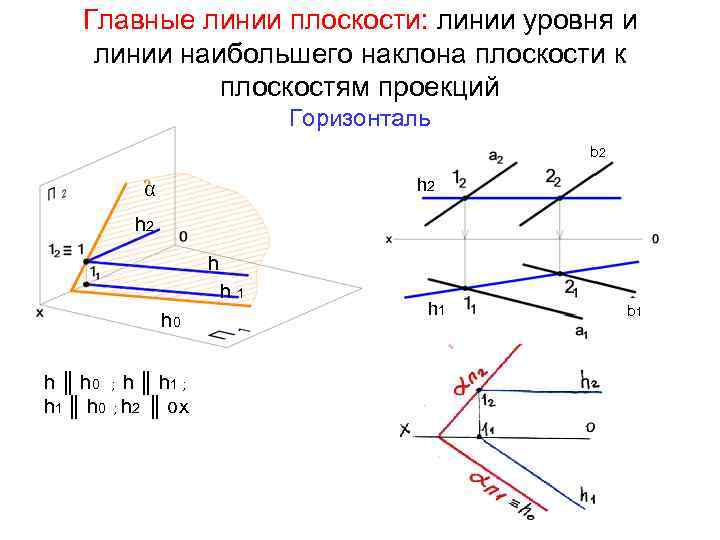
Главные линии плоскости: линии уровня и линии наибольшего наклона плоскости к плоскостям проекций Горизонталь b 2 h 2 α h 2 h h 1 h 0 h ║ h 0 ; h ║ h 1 ; h 1 ║ h 0 ; h 2 ║ ох h 1 b 1
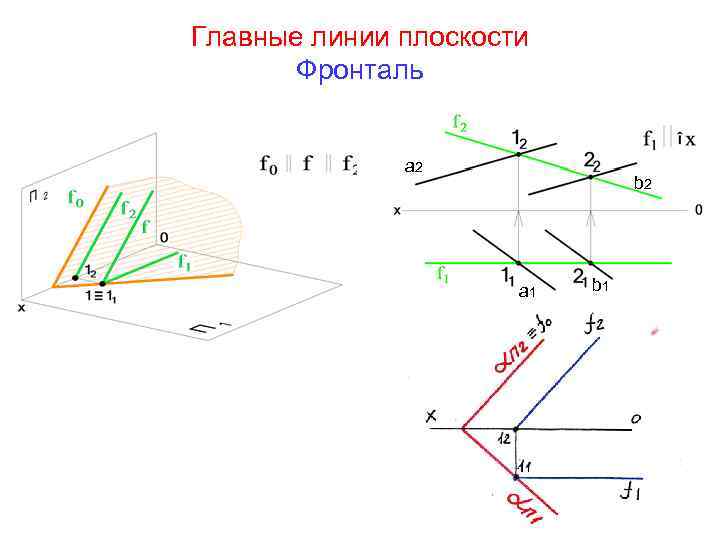
Главные линии плоскости Фронталь a 2 b 2 a 1 b 1

Линия наибольшего наклона плоскости- прямая, лежащая в плоскости, составляющая с плоскостью проекций максимальный угол и перпендикулярная соответствующей линии уровня (при определении угла наклона к П 1 – к горизонтали, при определении угла наклона к П 2 - к фронтали) Дана плоскость Р Р РП 1 α Определить угол наклона плоскости Р к плоскости проекций П 1 Пусть [ А В ] – линия наибольшего наклона плоскости Р Тогда [ А В ] ┴ РП 1 [ MN ] ║П 1 → [ А В ] ┴ [ MN ] [ МВ ] ║ П 1 ; ∟ МВА = ∟ М 1 В 1 А 1 = 90° [ А 1 В 1 ] ┴ [ M 1 N 1 ]; α = ∟ В А В 1

Определение угла наклона плоскости общего положения к плоскости проекций • Угол наклона плоскости общего положения к какой-либо плоскости проекций равен углу между натуральной величиной линии наибольшего наклона плоскости и ее проекцией на заданную плоскость проекций.

Определение угла наклона плоскости к горизонтальной плоскости проекций ∆Z h 2 H ∆Z h 1 Л. н. н. h 1 α Н. в. [ВО].

Взаимное расположение плоскостей Плоскости, параллельные между собой. a║c b b║d a 1 ║ c 1 b 1 ║ d 1 b 1 Плоскости параллельны между собой в том случае, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости 2
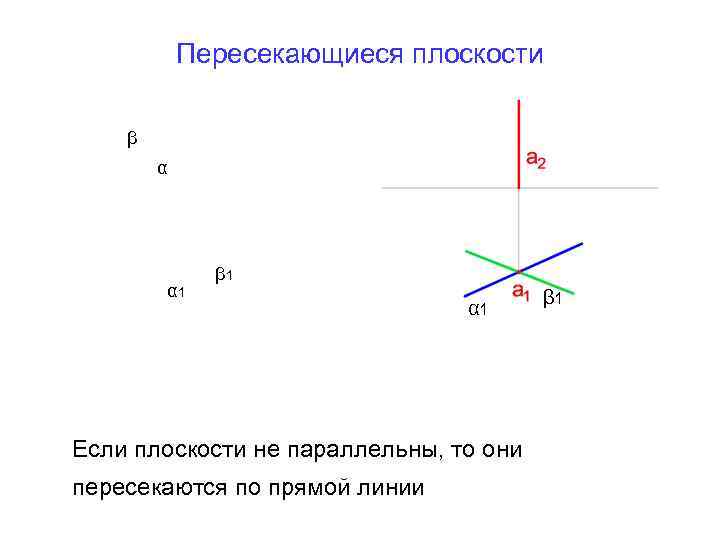
Пересекающиеся плоскости β α α 1 β 1 α 1 Если плоскости не параллельны, то они пересекаются по прямой линии β 1

Пересечение плоскости общего положения с горизонтально-проецирующей плоскостью Проекция линии пересечения α плоскости общего положения с проецирующей плоскостью совпадает со следом проецирующей плоскости. α 1

Пересечение плоскости общего положения с фронтально-проецирующей плоскостью Задача: Определить линию пересечения двух плоскостей. Решение: На П 2 проекция Δ 1 -2 -3 совпадает с проекцией линии пересечения двух плоскостей К 2 L 2, т. к. плоскость Δ 1 -2 -3 является проецирующей плоскостью. Определяем горизонтальную проекцию К 1 L 1. Определяем видимость искомых плоскостей на П 1 по конкурирующим точкам.

Пересечение двух плоскостей (метод плоскостей-посредников) α Σ Ω I β

Пересечение двух плоскостей 1. Рассекаем две заданные плоскости Σ и Ω вспомогательной плоскостью «α» . 2. Строим линии пересечения вспомогательной плоскости с заданными. 3. Находим точку пересечения полученных линий (·) I. 4. Рассекаем заданные плоскости второй вспомогательной плоскостью «β» . 5. Строим линии пересечения вспомогательной плоскости с заданными. 6. Находим точку пересечения полученных линий (·)2 7. Соединяем точки I и 2, получаем линию пересечения плоскостей.

Пересечение двух плоскостей b 2 α 2 b 1

Пересечение двух плоскостей b 2 α 2 β 2 b 1

Взаимное расположение прямой и плоскости Прямая принадлежит плоскости b b 1 b 2 b 1 Прямая принадлежит плоскости в том случае, если она проходит через две точки, принадлежащие этой плоскости.
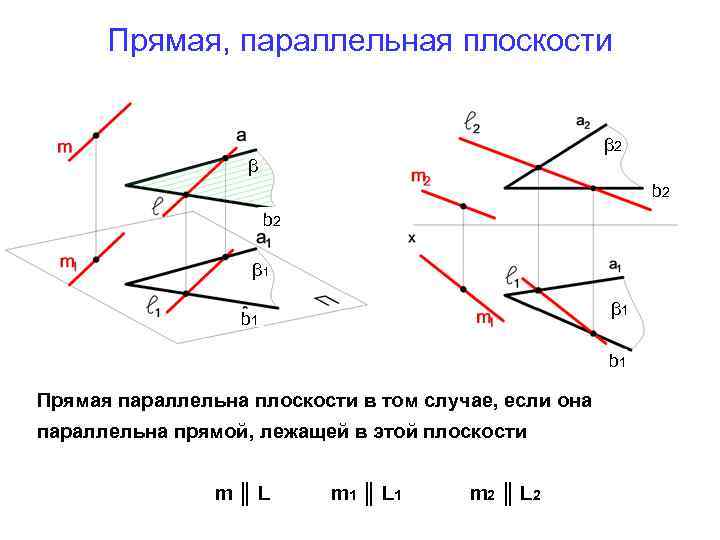
Прямая, параллельная плоскости β 2 β b 2 β 1 b 1 Прямая параллельна плоскости в том случае, если она параллельна прямой, лежащей в этой плоскости m║L m 1 ║ L 1 m 2 ║ L 2
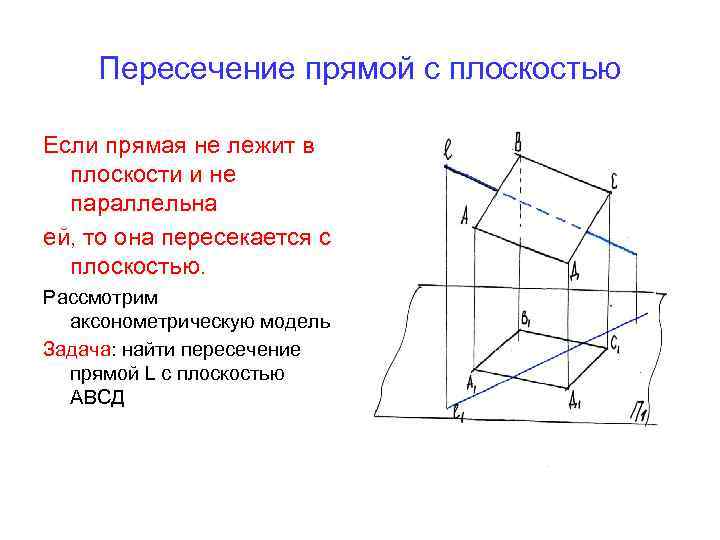
Пересечение прямой с плоскостью Если прямая не лежит в плоскости и не параллельна ей, то она пересекается с плоскостью. Рассмотрим аксонометрическую модель Задача: найти пересечение прямой L с плоскостью АВСД

Пересечение прямой с плоскостью 1. Заключаем прямую во вспомогательную проецирующую плоскость. 2. 2. Строим линию пересечения двух плоскостей: вспомогательной и заданной. 3. 3. Находим точку пересечения прямой и полученной линии пересечения. 4. 4. Определяем видимость прямой.
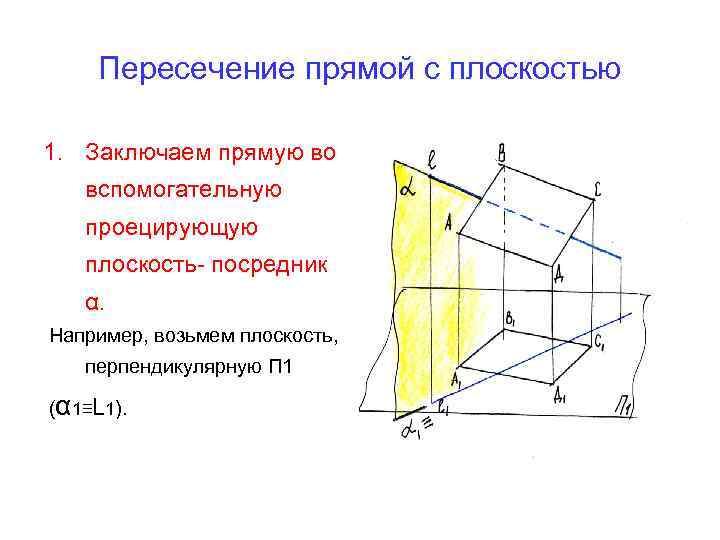
Пересечение прямой с плоскостью 1. Заключаем прямую во вспомогательную проецирующую плоскость- посредник α. Например, возьмем плоскость, перпендикулярную П 1 (α 1≡L 1).
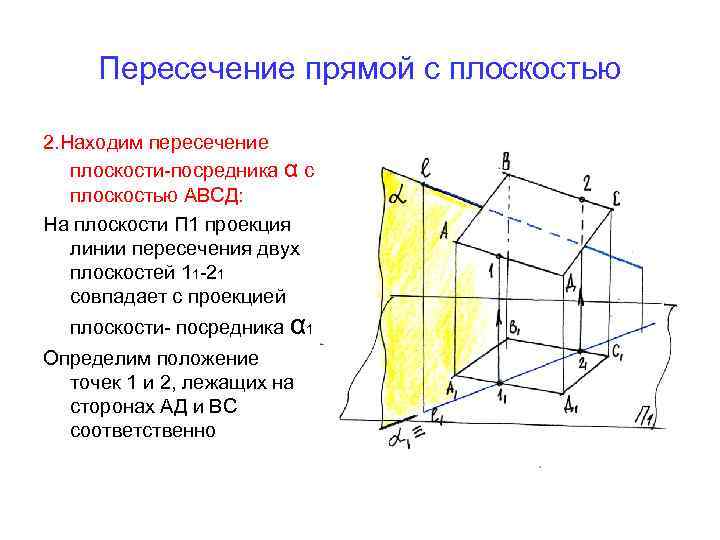
Пересечение прямой с плоскостью 2. Находим пересечение плоскости-посредника α с плоскостью АВСД: На плоскости П 1 проекция линии пересечения двух плоскостей 11 -21 совпадает с проекцией плоскости- посредника α 1 Определим положение точек 1 и 2, лежащих на сторонах АД и ВС соответственно
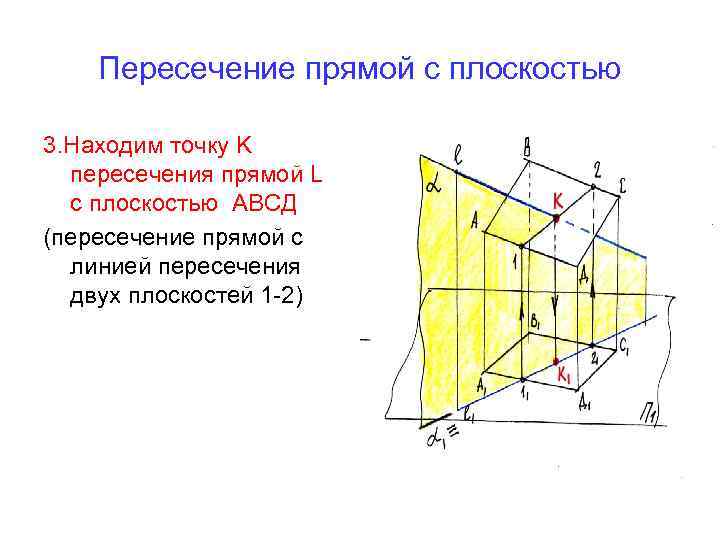
Пересечение прямой с плоскостью 3. Находим точку K пересечения прямой L с плоскостью АВСД (пересечение прямой с линией пересечения двух плоскостей 1 -2)
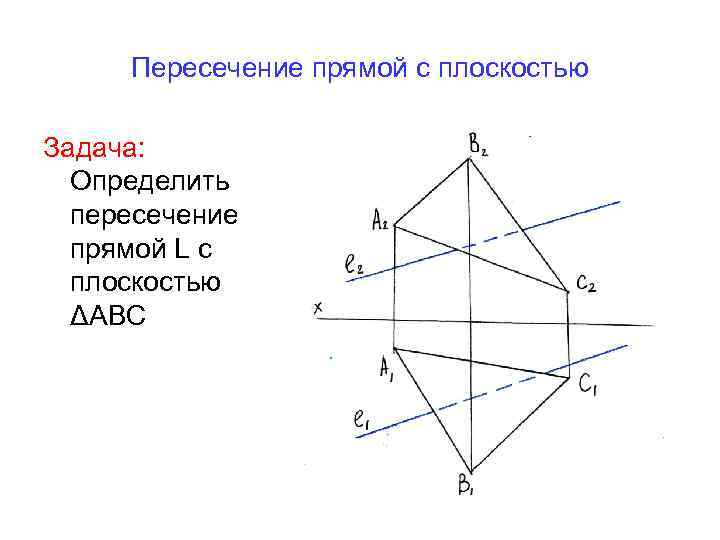
Пересечение прямой с плоскостью Задача: Определить пересечение прямой L с плоскостью ΔАВС
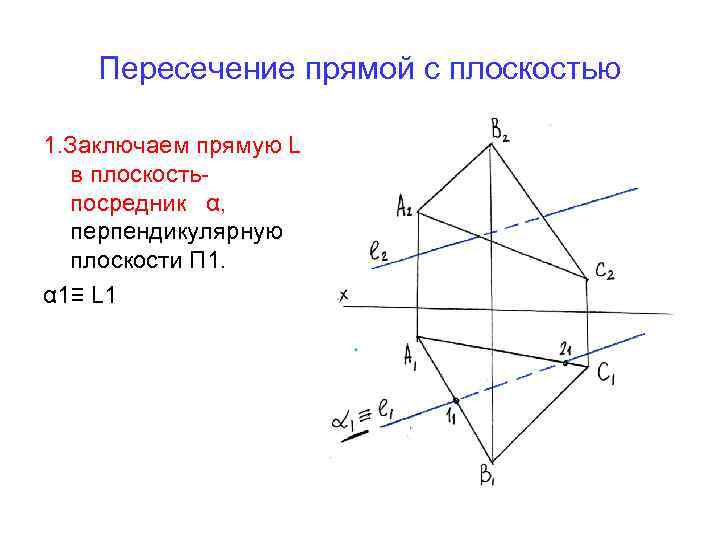
Пересечение прямой с плоскостью 1. Заключаем прямую L в плоскостьпосредник α, перпендикулярную плоскости П 1. α 1≡ L 1
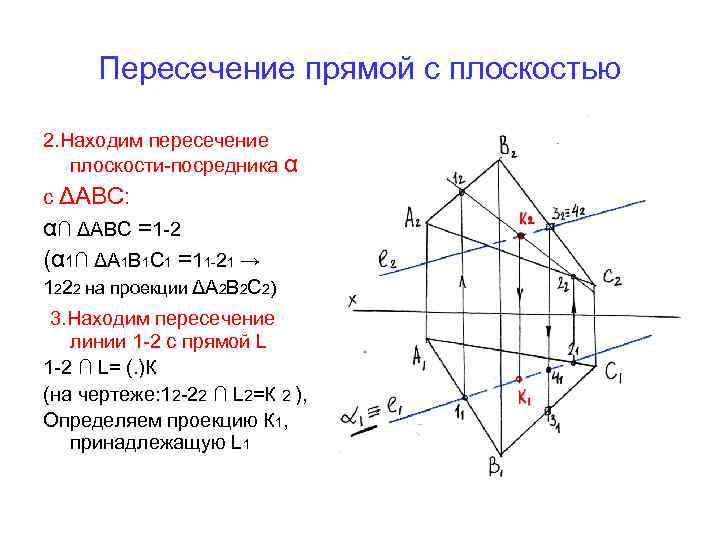
Пересечение прямой с плоскостью 2. Находим пересечение плоскости-посредника α с ΔАВС: α∩ ΔАВС =1 -2 (α 1∩ ΔА 1 В 1 С 1 =11 -21 → 1222 на проекции ΔА 2 В 2 С 2) 3. Находим пересечение линии 1 -2 с прямой L 1 -2 ∩ L= (. )К (на чертеже: 12 -22 ∩ L 2=К 2 ), Определяем проекцию К 1, принадлежащую L 1
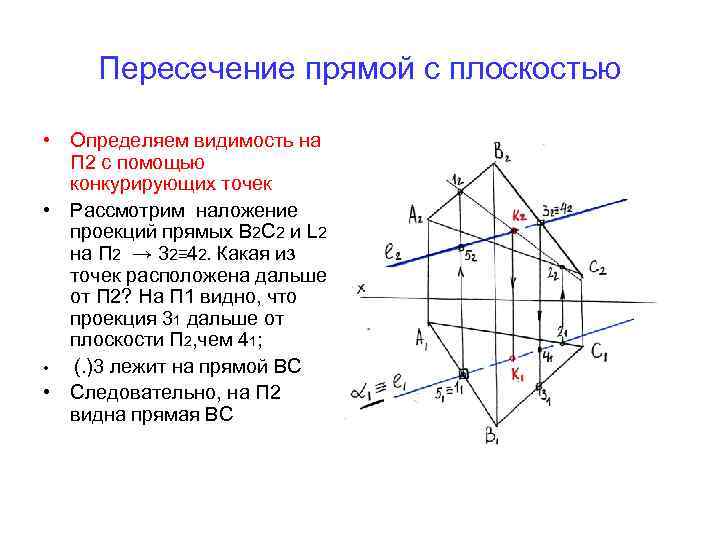
Пересечение прямой с плоскостью • Определяем видимость на П 2 с помощью конкурирующих точек • Рассмотрим наложение проекций прямых В 2 С 2 и L 2 на П 2 → 32≡ 42. Какая из точек расположена дальше от П 2? На П 1 видно, что проекция 31 дальше от плоскости П 2, чем 41; • (. )3 лежит на прямой ВС • Следовательно, на П 2 видна прямая ВС
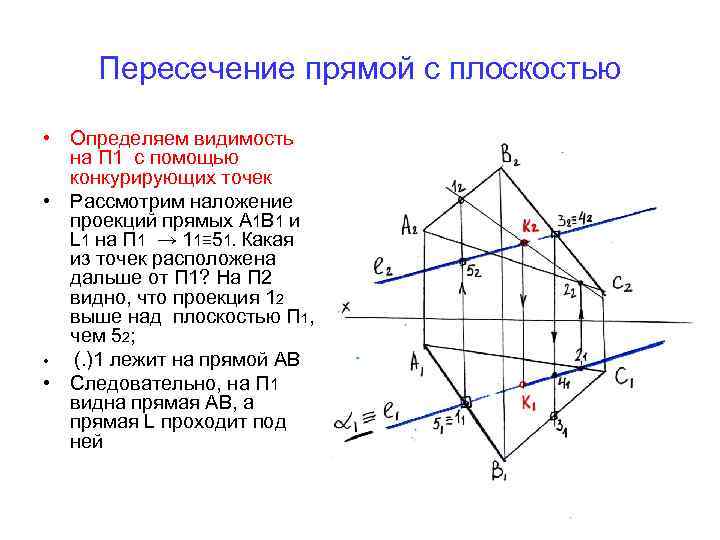
Пересечение прямой с плоскостью • Определяем видимость на П 1 с помощью конкурирующих точек • Рассмотрим наложение проекций прямых А 1 В 1 и L 1 на П 1 → 11≡ 51. Какая из точек расположена дальше от П 1? На П 2 видно, что проекция 12 выше над плоскостью П 1, чем 52; • (. )1 лежит на прямой АВ • Следовательно, на П 1 видна прямая АВ, а прямая L проходит под ней
Начерталка3.ppt