Лекция 3 Формализация понятия алгоритма Булевские функции

Лекция 3 Формализация понятия алгоритма. Булевские функции

нестрогое определение n алгоритм – точно определенная последовательность действий, обеспечивающая решение задач определенного класса для указанного класса исходных данных.

Формализация понятия алгоритм n n n Существует большое количество задач, вызывающих трудности создания алгоритма их решения или требующих значительного упрощения процедур их решения или расширения области применения известных алгоритмов и др. Существование таких задач требует формализовать понятие алгоритма. При этом выделяют 2 проблемы: возможно более строгое определение алгоритма, его свойства; изучение теоретических моделей алгоритмов и исследование проблемы алгоритмической разрешимости.

Главной целью n формализации понятия алгоритма является решение проблемы алгоритмической разрешимости различных математических задач, т. е. получение ответа на вопрос, существует ли алгоритм решения указанного класса задач.

Второй целью n – является определение элементарного шага алгоритма

Третьей целью n строгого определения понятия «алгоритм» является выбор наиболее эффективного алгоритма из нескольких возможных с теоретической и практической точек зрения

два класса задач n n 1. вычисление значений функций 2. распознавание принадлежности объекта заданному множеству

определение n Функция называется вычислимой, если существует алгоритм, вычисляющий ее значение.

определение n Множество называется разрешимым, если имеется алгоритм, позволяющий для любого объекта определить, принадлежит он данному множеству или нет.

Второй подход (А. Черч, Д. Гильберт, П. С. Новиков) n Эти ученые определили алгоритм через класс вычислимых (общерекурсивных) функций. Они все проблемы разделили на алгоритмически разрешимые и неразрешимые.

Третий подход представляют А. Тьюринг и Э. Л. Пост n Ими были описаны машины, с помощью которых можно было реализовать любой алгоритм.

Тезис Черча-Тьюринга n Любое разумное определение алгоритма, которое может быть предложено в будущем, окажется эквивалентным уже известным определениям.

Контрольные вопросы n n n 1. Зачем нужны булевы функции? 2. Почему можно автоматизировать процесс обработки информации? 3. Какова причина в необходимости формализации понятия «алгоритм» ? 4. Каковы возможные подходы к определению понятия алгоритм?

Проблема n n n А – множество элементов информации В – другое множество Ф – функция преобразования В А Ф

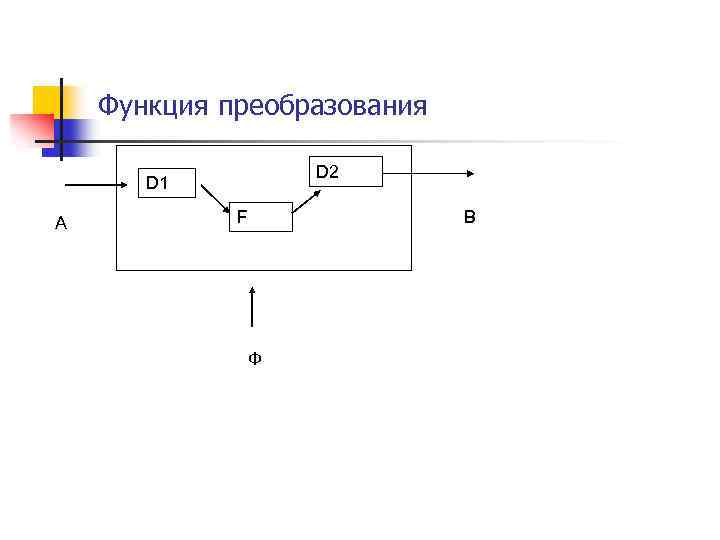
Функция преобразования D 2 D 1 A F B Ф

Ф = D 1*F*D 2 n n Нужно строить три функциональных преобразователя Пример (a 1, а 2, а 3, а 4, а 5 ) (в 1, в 2, в 3) 001, 010, 011, 100, 101 -> 01, 11, 00

Определение n n Обозн. : (0, 1)n = (x 1, x 2, …, xn) – вектор из двоичных цифр Функция f : (0, 1)n -> (0, 1), сопоставляющая двоичным векторам двоичное число, называется двоичной (или булевой) функцией. Основная задача – построение сложной булевой функции на основе простейших.

Функции от одной переменной F: X ->Y, X = (0, 1), Y = (0, 1) n n f 1(x) = 0 f 2(x) = 1 f 3(x) = x f 4(x) = ¬x (две константы, тождественная и функция отрицания)

Функции от двух переменных (16 шт) n F: X*Y -> Z , X, Y, Z = (0, 1) f(x, y)= x^y; xvy; x =>y; x+y; x↓y; x|y n конъюнкция, дизъюнкция, импликация (следование), эквивалентности, сложение по модулю 2 (ХОR), стрелка Пирса (НЕ-ИЛИ), штрих Шеффера (НЕ-И).

Теорема 1 n n Любая двоичная функция может быть представлена как суперпозиция трех функций И, ИЛИ, НЕ. (наз. Сложная функция или логическая формула)

Определение n n Функционально полным набором (базисом) будем называть такое множество функций, суперпозицией которых могут быть представлены любые булевы функции. И, ИЛИ, НЕ – являются базисом.

Определение n n n Представление булевой функции в форме дизъюнкции: F(x 1, x 2, …, xn) = K 1 v K 2 v. . v Kn , где каждый терм Кi представляет конъюнкцию двоичных переменных, с отрицанием или без них, наз. дизъюнктивной нормальной функцией Если каждый конъюнкт содержит по одной из всех переменных (с отрицанием или без), то форма представления функции называется совершенной. F(p, q, r) = ¬p¬q¬r v ¬pq¬r v p¬q¬r v pqr

Конъюктивная нормальная функция. Совершенная форма КНФ n Определяются аналогично ДНФ и СДНФ (симметрично).

Теорема 2 n Представление булевых функций в n Следствие n n n СДНФ, СКНФ единственно. Всякая аналитическая запись функции может быть преобразована в СДНФ или СКНФ. Алгоритм Устраняем все операции, кроме И, ИЛИ, НЕ (свойства функций) Преобразуем к одиночным отрицаниям (свойства функций). Преобразуем к нормальной форме (свойства функции)

Формы представления булевских функций n n Табличная (таблица истинности) аналитическая запись семантическое дерево бинарная диаграмма решения

Реализация n Физические устройства дискретного отображения 0 и 1 -- это ключ-реле (переключатели)

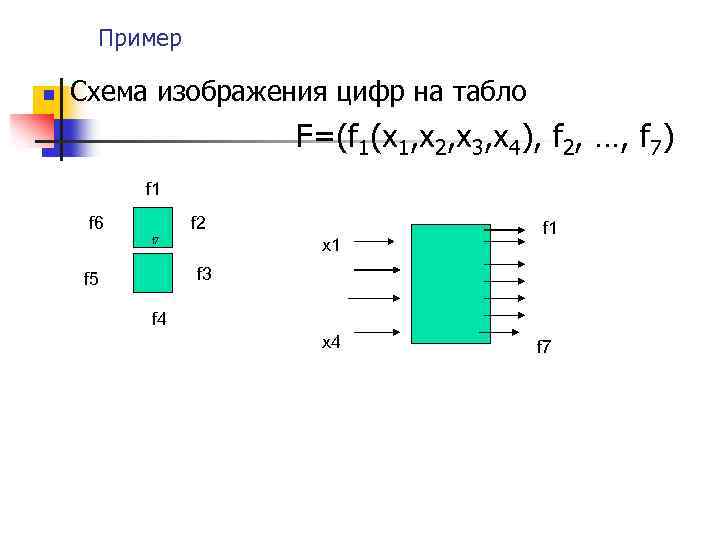
Пример n Схема изображения цифр на табло F=(f 1(x 1, x 2, x 3, x 4), f 2, …, f 7) f 1 f 6 f 2 f 7 x 1 f 3 f 5 f 4 x 4 f 7

Минимизация Метод Квайна Функция представляется в СДНФ и к ней применяются все возможные операции склеивания, а затем поглощения многократно. n Карта Карно Двумерная табличная форма с определенными манипуляциями. n

Пороговая логика n n n Пример формального нейрона Y=1, если ∑ xi*wi ≥ P, где P – пороговое значение, иначе У=0 x 1 w 1 y w 2 x 2

Вывод n n n Обработку дискретной информации можно свести к построению булевой функции. Вычисление любой булевой функции можно автоматизировать. Обработку дискретной информации можно автоматизировать на основе алгоритма.