Лекция 3 Двойственные задачи ЛП Денисова С Т

Лекция 3. Двойственные задачи ЛП Денисова С. Т. Старший преподаватель n кафедры ММи. МЭ n n

План: n n n Двойственные задачи ЛП. Теоремы двойственности. Примеры двойственных задач. Анализ решения ЗЛП с помощью теории двойственности: 1)нахождение дефицитных ресурсов, 2) анализ на чувствительность (интервалы изменений коэффициентов целевой функции, при которых оптимальные значения переменных остаются неизменными)

Двойственные задачи ЛП n Прямая задача n F(X)= n n n Двойственная задача Z(Y)= 3

Алгоритм составления двойственной задачи: n n Приводят все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задач ищут максимум линейной функции, то все неравенства системы ограничений приводят к виду «≤» , а если минимум – к виду «≥» . Составляют расширенную матрицу системы А 1, в которую включают матрицу коэффициентов при переменных, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции. Находят матрицу А, транспонированную к матрице А 1. Формулируют двойственную задачу на основании полученной матрицы А и условия неотрицательности переменных. 4

Основное неравенство теории двойственности n n n Пусть имеется пара двойственных задач. Для любых допустимых решений Х= (x 1, x 2, …, хn) и У=(y 1, y 2, …, ym) исходной и двойственной задач справедливо неравенство: F(X) ≤ Z(Y) 5

Первая (основная) теорема двойственности. n n Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причём оптимальные значения их целевых функций равны: Fmax=Zmin или F(X*) =Z(Y*) (1) 6

Вторая теорема двойственности n n Пусть X*=(x 1* , x 2* , …. . xn* ) - план исходной задачи и Y*=(y 1* , y 2* , …. . yn* ) - план двойственной задачи. X*и Y* являются оптимальными только тогда, когда для любого j, (j=1, 2, . . n) выполняется равенство 7

Задача 1. Для производства трёх изделий А, В, С используются три вида сырья. каждый из них используется в объёме, не превышающем 180, 210 и 236 кг. Определить план выпуска изделий, обеспечивающий получение оптимального дохода при условии, что потребление ресурсов по каждому виду продукции не превзойдёт имеющихся запасов. Экономико-математическая модель задачи: F= 10 x 1+14 x 2+12 x 3→max x 1≥ 0, x 2≥ 0, х3≥ 0. 8

Задача (двойственная) Найти такой набор цен ресурсов, при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производ-стве каждого вида продукции будут не менее прибыли от реализации этой продукции. Z(У)= 180 y 1+210 y 2+236 y 3→min y 1≥ 0, у2≥ 0, у3≥ 0. Симметричная задача 9

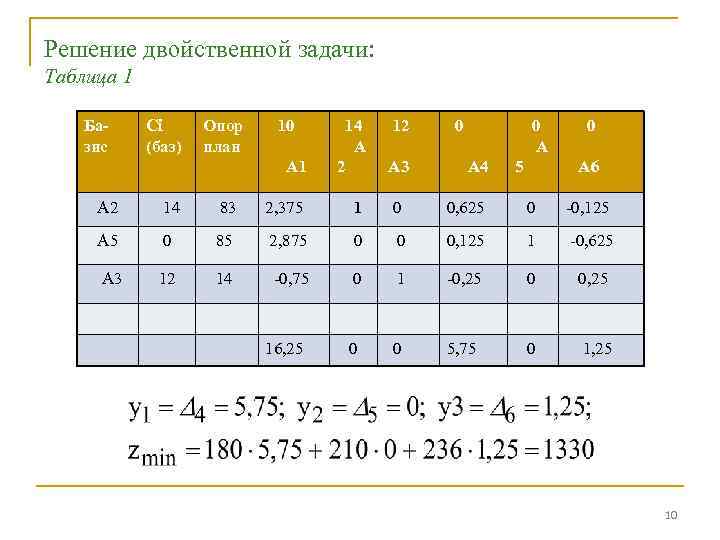Решение двойственной задачи: Таблица 1 Базис Сi (баз) Опор план 10 А 1 14 А 2 12 А 3 0 0 А А 4 5 0 А 6 А 2 14 83 2, 375 1 0 0, 625 0 -0, 125 А 5 0 85 2, 875 0 0 0, 125 1 -0, 625 А 3 12 14 -0, 75 0 1 -0, 25 0 0 5, 75 0 1, 25 16, 25 10

Решение двойственной задачи: 11

Анализ решения ЗЛП с помощью теории двойственности n Задача. Фабрика выпускает продукцию двух видов П 1 и П 2. Для производства продукции используются три вида сырья А, В, С, максимально возможные запасы их составляют 6, 8 и 5 тонн соответственно. Расходы сырья А, В, С на 1 тыс. изделий П 1 и П 2 приведены в таблице. Изучение рынка сбыта показало, что суточный спрос на изделия П 2 не превышает спроса на изделия П 1 более чем на 1 тыс. шт. Установлено, что спрос на изделия П 2 не превышает 2 тыс. шт. в сутки. Какое количество изделий 9 в тыс. шт. ) должна производить фабрика, чтобы доход от реализации продукции был максимальным? 12

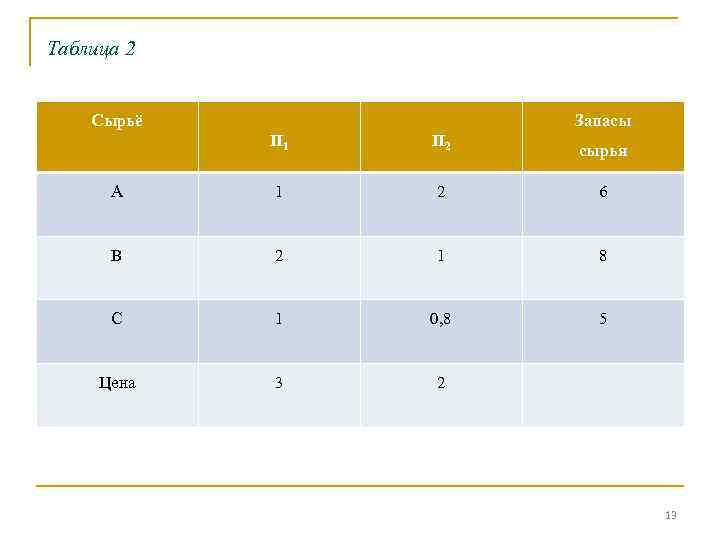Таблица 2 Сырьё Запасы П 1 П 2 сырья А 1 2 6 В 2 1 8 С 1 0, 8 5 Цена 3 2 13

Экономико-математические модели задач: F= 3 x 1+2 x 2→max; при ограничениях: n х1+2 х2≤ 6 n 2 х1+х2≤ 8 х1+0, 8 х2≤ 5 - х1+х2≤ 1 х2≤ 2 x 1≥ 0, x 2≥ 0. Z=6 y 1+8 y 2+5 y 3+y 4+2 y 5→min n y 1+2 y 2+y 3 -y 4 ≥ 3 2 y 1+y 2+y 3+y 4 +y 5 ≥ 2 y 1 ≥ 0, y 2 ≥ 0, . . y 5 ≥ 0 14

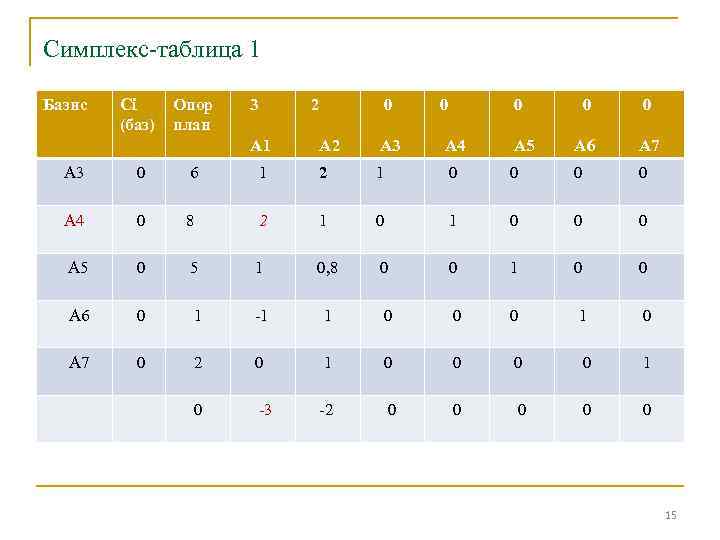Симплекс-таблица 1 Базис Сi (баз) Опор план 3 2 А 1 0 0 0 А 2 А 3 А 4 А 5 А 6 А 7 А 3 0 6 1 2 1 0 0 А 4 0 8 2 1 0 0 0 А 5 0 5 1 0, 8 0 0 1 0 0 А 6 0 1 -1 1 0 0 0 1 0 А 7 0 2 0 1 0 -3 -2 0 0 0 15

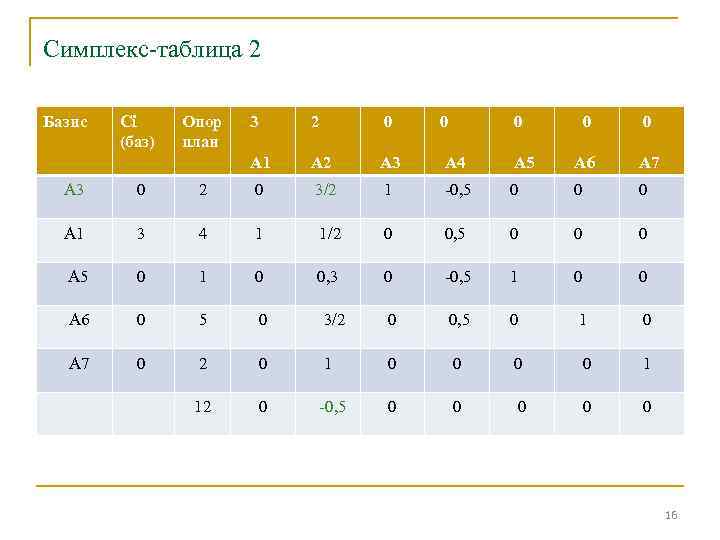Симплекс-таблица 2 Базис Сi (баз) Опор план 3 2 0 0 0 А 1 А 2 А 3 А 4 А 5 А 6 А 7 А 3 0 2 0 3/2 1 -0, 5 0 0 0 А 1 3 4 1 1/2 0 0, 5 0 0 0 А 5 0 1 0 0, 3 0 -0, 5 1 0 0 А 6 0 5 0 3/2 0 0, 5 0 1 0 А 7 0 2 0 1 0 0 1 12 0 -0, 5 0 0 0 16

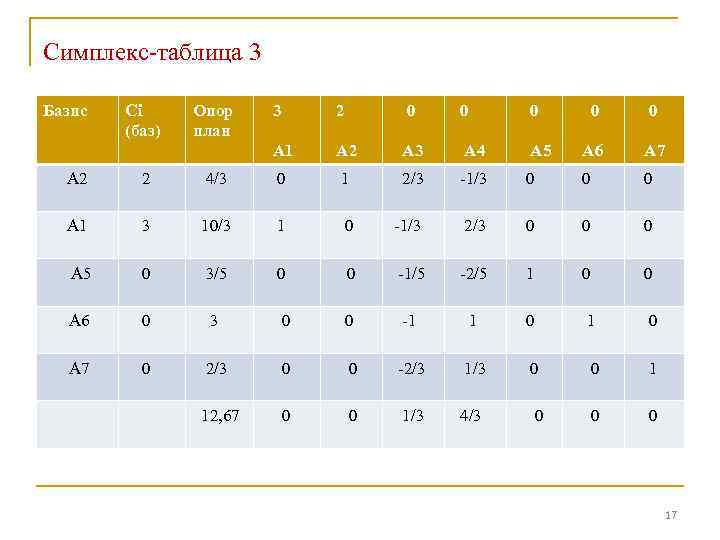Симплекс-таблица 3 Базис Сi (баз) Опор план 3 2 0 0 0 А 1 А 2 А 3 А 4 А 5 А 6 А 7 А 2 2 4/3 0 1 2/3 -1/3 0 0 0 А 1 3 10/3 1 0 -1/3 2/3 0 0 0 А 5 0 3/5 0 0 -1/5 -2/5 1 0 0 А 6 0 3 0 0 -1 1 0 А 7 0 2/3 0 0 -2/3 1/3 0 0 1 12, 67 0 0 1/3 4/3 0 0 0 17

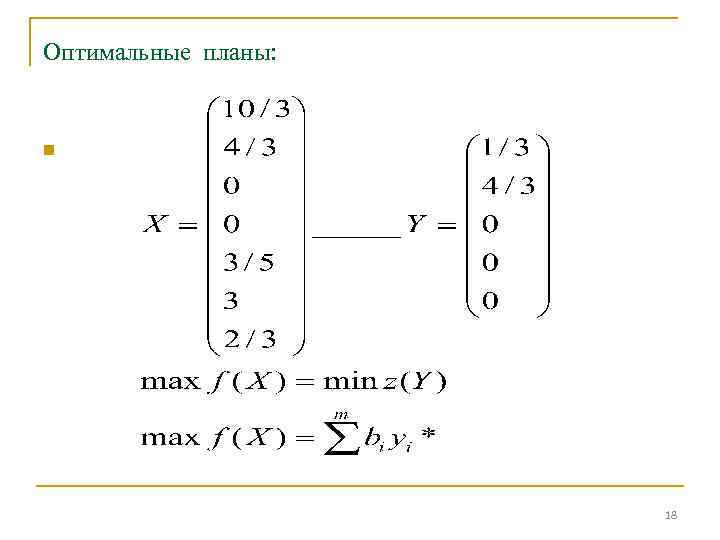Оптимальные планы: n 18

Анализируя вектор У, сделаем выводы: n При увеличении запаса сырья А на 1 т. доход от реализации продукции увеличится на 1/3 тыс. руб. , а при увеличении запаса сырья В на 1 т. доход от реализации продукции увеличится на 4/3 тыс. руб. Изменение запаса С или изменение в соотношениях спроса не приводят к изменению дохода. Ресурсы А и В являются дефицитными, ресурс С - недифицитный. 19

С 1=3+ С 1; 1 =0 ; 2 =0 20

Интервалы изменений коэффициентов целевой функции: n n n Выполнив аналогичные преобразования с С 2 , получим пределы изменения С 2 , при которых будет выгодно выпускать продукцию П 2 -1/2≤ С 2 ≤ 4 2 -1/2≤ С 2 ≤ 2+ 4 3/2≤ С 2 ≤ 6 Ответ: 1 ≤ С 1 ≤ 4, 1, 5 ≤ С 2 ≤ 6. n n 21