Лекция 3 Арифметические основы ЭВМ Вопросы Знаковые

Лекция 3. Арифметические основы ЭВМ Вопросы: • Знаковые системы; • Системы счисления; • Двоичная, восьмеричная, десятичная, шестнадцатеричная системы счисления

Знаковые системы Это системы однообразно интерпретируемых и трактуемых сообщений/сигналов. Они состоят из алфавита и правил составления конструкций из символов. Примеры: естественные языки, системы счисления и пр.

Системы счисления Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.

Системы счисления Любая предназначенная для практического применения СС должна обеспечивать: • возможность представления любого числа в рассматриваемом диапазоне величин; • единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина); • простоту оперирования числами

Системы счисления Человек начинал считать, пользуясь унарной системой счисления. Для записи чисел применялся только один вид знаков - палочка. Каждое число в такой системе обозначается с помощью строки, составленной из отдельных палочек.

Системы счисления Алфавиты двоичной системы - 0, 1 восьмеричной - 0, 1, 2, 3, 4, 5, 6, 7 десятичной - 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 шестнадцатеричной- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Системы счисления В зависимости от способов изображения чисел цифрами, системы счисления делятся на непозиционные и позиционные. Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ей позиции в изображении числа. Позиционной системой счисления называется такая, в которой количественное значение каждой цифры зависит от её позиции в числе

Системы счисления Количество различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления - “p”. Любое число N в позиционной системе счисления с основанием может быть представлено в виде полинома от основания p.

Перевод чисел из десятичной системы счисления в другие Пример: Выполнить перевод числа 1910 в двоичную систему счисления:

Перевод чисел из других систем счисления в десятичную Пример: перевести число 100112 в десятичную систему счисления. 10011= 1*20+1*21+0*22+0*23+1*24=1+2 +16=1910

Связь двоичной, восьмеричной и шестнадцатеричной систем счисления Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) или четырехразрядным двоичным числом (тетрадой), при этом отбрасывают ненужные нули в старших и младших разрядах.

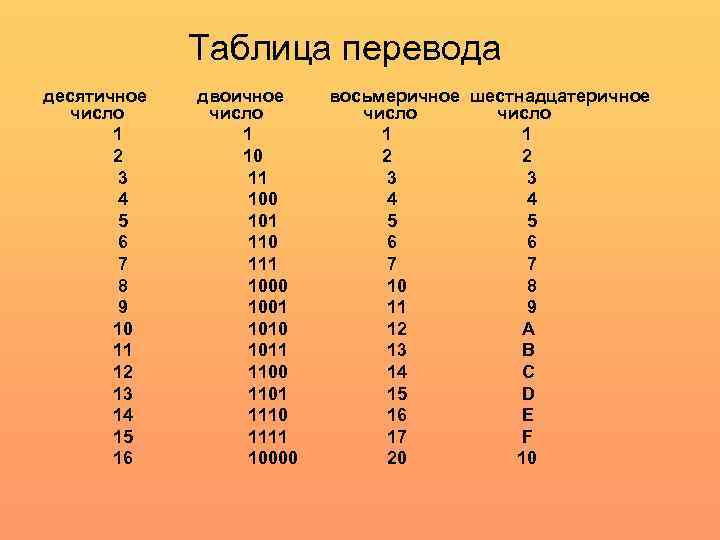Таблица перевода десятичное число 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 двоичное число 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 восьмеричное шестнадцатеричное число 1 1 2 2 3 3 4 4 5 5 6 6 7 7 10 8 11 9 12 A 13 B 14 C 15 D 16 E 17 F 20 10

Связь двоичной, восьмеричной и шестнадцатеричной систем счисления Пример: Выполнить перевод числа 100112 в шестнадцатеричную систему счисления. Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Далее пользуемся таблицей перевода и получаем 1316