Лекция 3 «АНАЛИЗ ПРОЦЕССОВ МЕТОДАМИ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ»

Лекция 3 «АНАЛИЗ ПРОЦЕССОВ МЕТОДАМИ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ» Преподаватель: Рыхлов Владимир Олегович Москва – 2014

УЧЕБНЫЕ ВОПРОСЫ: 1. Общая характеристика систем массового обслуживания, их классы. 2. Задачи управления, решаемые методами теории массового обслуживания

Теория массового обслуживания – раздел исследования операций (теории вероятностей), целью которого является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслужива-ние, поступающих в систему и выходящие из нее, длительности ожидания и длины очередей.

Задача теории массового обслуживания – установле-ние математических зависимостей между характеристи-ками потока требований на обслуживание, производи-тельностью одиночного средства обслуживания, их коли-чеством и показателем эффективности системы обслужи-вания в целом.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Системой массового обслуживания (обслуживающей системой), называется совокупность каналов обслуживания, а также очередь, если она допустима. Последовательность различных событий в системе называют потоком. В СМО различают следующие потоки: - входящий - последовательность нуждающихся в обслужи-вании и поступающих в обслуживающую систему заявок; - выходящий обслуженных заявок - последовательность заявок на выходе системы, получивших обслуживание; - выходящий необслуженных заявок - последовательность заявок на выходе системы, получивших отказ в обслуживании.

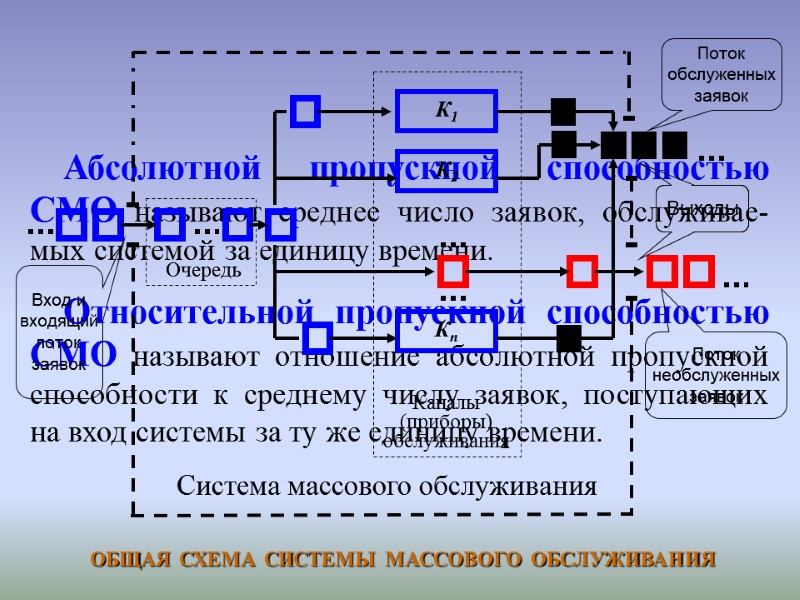
Абсолютной пропускной способностью СМО называют среднее число заявок, обслуживае-мых системой за единицу времени. Относительной пропускной способностью СМО называют отношение абсолютной пропускной способности к среднему числу заявок, поступающих на вход системы за ту же единицу времени.

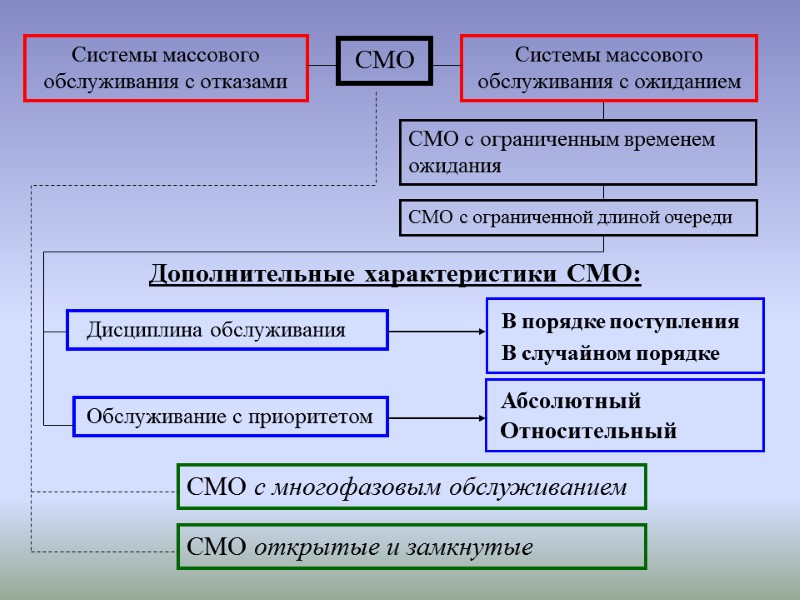
ДОПОЛНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СМО: 1. Дисциплина обслуживания – заявки могут обслуживаться либо в порядке поступления, либо в случайном порядке. 2. Обслуживание с приоритетом – некоторые заявки обслу-живаются вне очереди. Приоритет может быть как абсолютным - заявка с более высоким приоритетом "вытесняет" из-под обслуживания заявку с низшим, так и относительным - заявка с более высоким приоритетом занимает лучшее место в очереди. 3. СМО с многофазовым обслуживанием состоят из несколь-ких последовательных этапов. 4. СМО открытые и замкнутые: в открытой СМО характе-ристики потока заявок не зависят от состояния самой системы (числа занятых каналов), а в замкнутой СМО – зависят.

ХАРАКТЕРИСТИКИ ПОТОКА СОБЫТИЙ (ЗАЯВОК) Графическая иллюстрация потока случайных событий Интенсивность потока событий λ - среднее число событий, появляющихся за единицу времени. 1. Если λ = λ (t) = const, т.е. интенсивность событий не зависит от времени, то поток принято называть стационарным. 2. Поток событий называют ординарным, если за сколь угодно малый отрезок времени вероятность появления одного события гораздо больше вероятности появления двух и более. 3. Если в потоке вероятность появления некоторого числа событий за фиксированный промежуток времени не зависит от числа наступивших в любой другой не пересекающийся с данным, промежутком времени, то он называется потоком без последействия.

Если поток событий одновременно стационарен, ордина-рен и без последействия, то его называют простейшим или стационарным пуассоновским, а при отсутствии стационарности, соответственно, - нестационарным пуас-соновским. Вероятность наступления ровно κ событий (κ =1,2,…, n) за время τ подчиняется закону Пуассона: где α = α (τ) = λ τ – математическое ожидание числа событий за время τ для простейшего потока; – для нестационарного пуассоновского потока

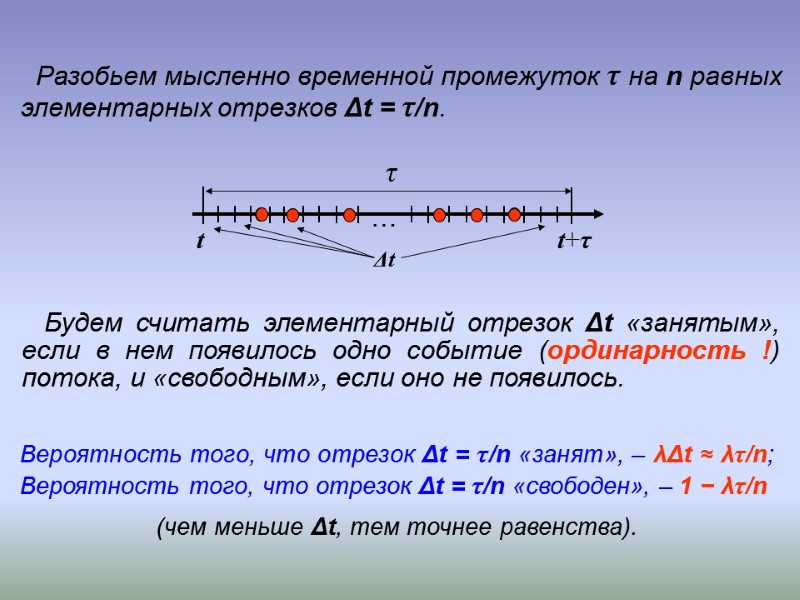
Разобьем мысленно временной промежуток τ на n равных элементарных отрезков Δt = τ/n. t t+τ τ Вероятность того, что отрезок Δt = τ/n «занят», – λΔt ≈ λτ/n; Вероятность того, что отрезок Δt = τ/n «свободен», – 1 − λτ/n (чем меньше Δt, тем точнее равенства). … Δt Будем считать элементарный отрезок Δt «занятым», если в нем появилось одно событие (ординарность !) потока, и «свободным», если оно не появилось.

Число занятых элементарных отрезков, т.е. число X событий на всем временном промежутке τ, можно рассматривать как случай-ную величину, имеющую биномиальный закон распределения *: с параметрами n и р = λτ/n . * Постоянство вероятности наступления события («занятости отрезка») в каждом испытании обеспечивается стационарностью потока, а независимость испытаний отсутствием последействия.

ХАРАКТЕРНЫЕ ЧЕРТЫ ПРОСТЕЙШЕГО ПОТОКА СМО с простейшими потоками имеет наиболее простое математическое описание; Предельное свойство простейшего потока: При наложении (суперпозиции) достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток близкий к простейшему, с интенсивностью, равной сумме интенсивностей входящих потоков. "Граничное свойство" простейшего потока: Если созданная СМО обладает необходимыми характерис-тиками эффективности для простейших потоков, то и для других потоков она будет функционировать с не меньшей эффективностью.

Показатели качества работы систем массового обслу-живания наряду с параметрами входящего потока во многом зависят от числа и работоспособности каналов обслу-живания, порождающих простейший поток обслуженных заявок интенсивностью μ. Время, затрачиваемое на обслуживание одной заявки (интервал Т между двумя произвольными соседними событиями стационарного пуассоновского потока), является случайной величиной, распределений по показательному (экспоненциальному) закону. ВРЕМЕННЫЕ ПОКАЗАТЕЛИ ПРОЦЕССА ОБСЛУЖИВАНИЯ

Плотность распределения описывается формулой: Таким образом, интервал Т между двумя произвольными соседними событиями простейшего потока имеет показательное (экспоненциальное) распределение, для которого: где - интенсивность потока обслуженных заявок (выходящего потока); - среднее время обслуживания одной заявки. Функция распределения равна:

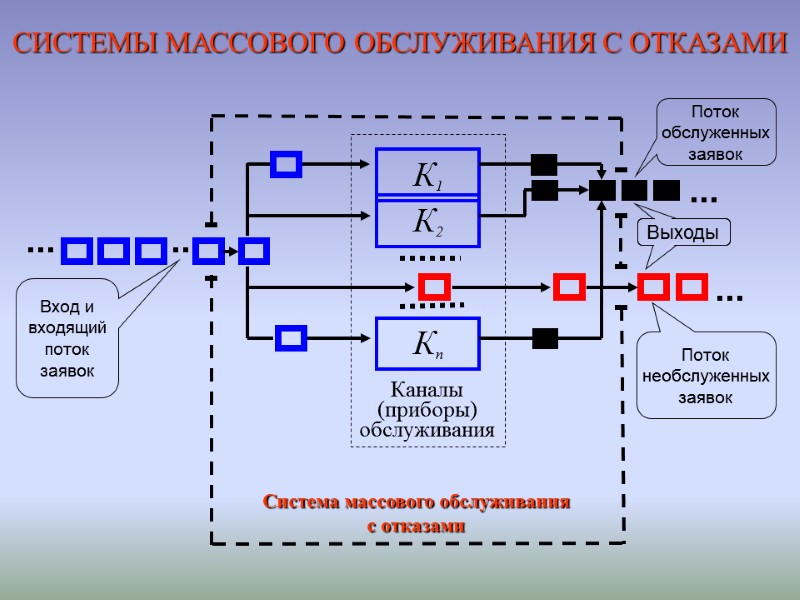
Размеченный граф состояний СМО с отказами λ μ λ λ λ λ λ 2μ kμ (k+1)μ (n-1)μ nμ

Размеченный граф состояний СМО с отказами Система дифференциальных уравнений Колмогорова - Чепмена Правило составления уравнений Колмогорова-Чепмена Производная вероятности состояния равна разности вероятностных потоков, входящих в вершину графа, со-ответствующую этому состоянию, и выходящих из нее.

СИСТЕМА ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ для финальных вероятностей (система уравнений ЭРЛАНГА):

где ρ = λ /μ – «приведенная интенсивность потока заявок» – отношение интенсивностей входящего и выходящего потоков (среднее число заявок, приходящих за среднее время обслуживания одной заявки). Данные зависимости называют формулами Эрланга - в честь основателя теории массового обслуживания. k=1,2,…n или Решение системы уравнений Эрланга:

Пример. Имеется один канал, на который поступает поток заявок с интенсивностью λ. Поток обслуживании имеет интенсивность μ. Все потоки простейшие. Найти предельные вероятности состояний системы и показатели ее эффективности. Абсолютная пропускная способность – что определяет среднее относительное время пребывания систе-мы в состоянии S0 (канал свободен) и S1 (канал занят), т.е. определяют соответственно Q – относительную пропускную способность системы и вероятность отказа Ротк : Решение.

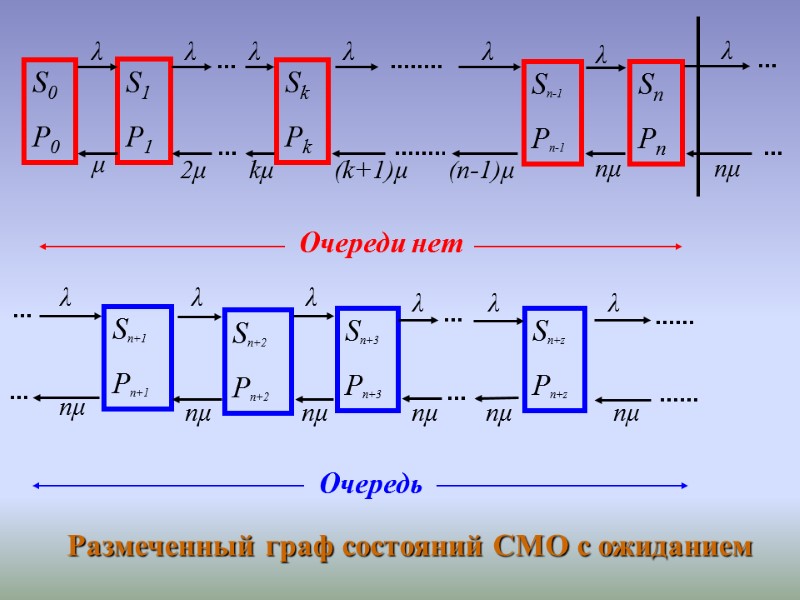
Система дифференциальных уравнений Колмогорова-Чепмена:

Характеристики эффективности СМО с ожиданием: Среднее число занятых каналов: Средняя длина очереди: Среднее время ожидания в очереди: Среднее время пребывания заявок в системе (ожидание в очереди и обслуживание): Коэффициент занятости каналов обслуживания:

Задачи управления, решаемые методами теории массового обслуживания ВТОРОЙ ВОПРОС

ЗАДАЧИ УПРАВЛЕНИЯ, РЕШАЕМЫЕ МЕТОДАМИ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ: 1. Рациональная организация функционирования различных систем обслуживания (ремонтные и снабженческие системы, ресурсное обеспечение и т.п.). 2. Оценка качества организации систем управления (системы сбора, передачи и обработки информации, организация и взаимосвязь органов управления и т.п.). 3. Математическое моделирование процессов различных действий, физический смысл которых допускает применение рассмотренного выше математического аппарата.