Механика_ЛК_3.pptx
- Количество слайдов: 36
 Лекция 3 1
Лекция 3 1
 Содержание предыдущей лекции Динамика поступательного движения. Закон сохранения импульса. • • Инерциальные системы отсчета. Законы Ньютона. Масса, импульс, сила. Уравнение движения материальной точки. Понятие замкнутой системы. Закон сохранения импульса. Центр масс механической системы, закон движения центра масс. • Движение тел переменной массы. Уравнение Мещерского. 2
Содержание предыдущей лекции Динамика поступательного движения. Закон сохранения импульса. • • Инерциальные системы отсчета. Законы Ньютона. Масса, импульс, сила. Уравнение движения материальной точки. Понятие замкнутой системы. Закон сохранения импульса. Центр масс механической системы, закон движения центра масс. • Движение тел переменной массы. Уравнение Мещерского. 2
 Контрольный вопрос Вы прижимаете учебник по физике к вертикальной стене. Сила трения, действующая со стороны стены на учебник, направлена: а) вниз, б) вверх, в) в сторону книги, г) в сторону стены. Сила, с которой Вы прижимаете учебник к стенке компенсируется упругой силой, действующей на Вас со стороны учебника и направленной горизонтально. Сила трения между учебником и стенкой направлена вверх и не дает учебнику упасть вниз под действием силы тяжести. а) 3
Контрольный вопрос Вы прижимаете учебник по физике к вертикальной стене. Сила трения, действующая со стороны стены на учебник, направлена: а) вниз, б) вверх, в) в сторону книги, г) в сторону стены. Сила, с которой Вы прижимаете учебник к стенке компенсируется упругой силой, действующей на Вас со стороны учебника и направленной горизонтально. Сила трения между учебником и стенкой направлена вверх и не дает учебнику упасть вниз под действием силы тяжести. а) 3
 Содержание сегодняшней лекции Динамика поступательного движения. Закон сохранения импульса. • Движение тел переменной массы. Формула Циолковского. Механическая энергия • Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией. • Консервативные и неконсервативные силы. • Работа и кинетическая энергия. • Закон сохранения полной механической энергии в поле потенциальных сил. 4
Содержание сегодняшней лекции Динамика поступательного движения. Закон сохранения импульса. • Движение тел переменной массы. Формула Циолковского. Механическая энергия • Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией. • Консервативные и неконсервативные силы. • Работа и кинетическая энергия. • Закон сохранения полной механической энергии в поле потенциальных сил. 4
 - уравнение движения тела с переменной массой Движение тел переменной массы Пусть тогда Прямолинейное движение ракеты в направлении, противоположном направлению скорости газовой струи 5
- уравнение движения тела с переменной массой Движение тел переменной массы Пусть тогда Прямолинейное движение ракеты в направлении, противоположном направлению скорости газовой струи 5
 Движение тел переменной массы Пусть скорость газовой струи постоянна, тогда Зависимость постоянной интегрирования С от начальных условий полета. Пусть при t = 0 v = 0, тогда и 6
Движение тел переменной массы Пусть скорость газовой струи постоянна, тогда Зависимость постоянной интегрирования С от начальных условий полета. Пусть при t = 0 v = 0, тогда и 6
 Движение тел переменной массы формула Циолковского для нерелятивистских скоростей. Обосновал использование ракет для полётов в космос, пришёл к выводу о необходимости использования «ракетных поездов» — прототипов многоступенчатых ракет. Российский и советский ученый Э. К. Циолковский (1857 -1935) 7
Движение тел переменной массы формула Циолковского для нерелятивистских скоростей. Обосновал использование ракет для полётов в космос, пришёл к выводу о необходимости использования «ракетных поездов» — прототипов многоступенчатых ракет. Российский и советский ученый Э. К. Циолковский (1857 -1935) 7
 Движение тел переменной массы Достижение первой космической скорости. Cкорость газовой струи, км/с m 0 / m 1 2 4 2980 54, 6 7, 39 Возможность повышения скорости газовой струи за счет увеличения Т и уменьшения молекулярной массы газа Необходимость учета релятивистских поправок. 8
Движение тел переменной массы Достижение первой космической скорости. Cкорость газовой струи, км/с m 0 / m 1 2 4 2980 54, 6 7, 39 Возможность повышения скорости газовой струи за счет увеличения Т и уменьшения молекулярной массы газа Необходимость учета релятивистских поправок. 8
 Движение тел переменной массы Перспективы: фотонная ракета, движущаяся за счет излучения двигателем ракеты светового потока. 9
Движение тел переменной массы Перспективы: фотонная ракета, движущаяся за счет излучения двигателем ракеты светового потока. 9
 Механическая энергия 10
Механическая энергия 10
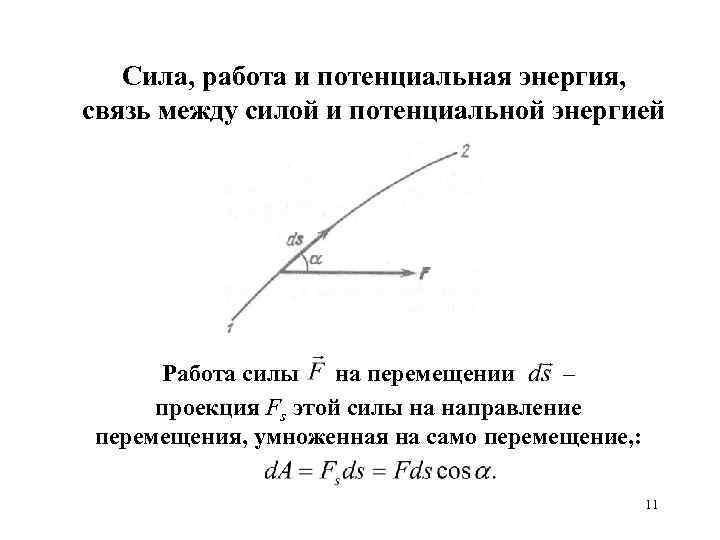 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Работа силы на перемещении – проекция Fs этой силы на направление перемещения, умноженная на само перемещение, : 11
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Работа силы на перемещении – проекция Fs этой силы на направление перемещения, умноженная на само перемещение, : 11
 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией 12
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией 12
 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией 13
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией 13
 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией 14
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией 14
 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией 1 Джоуль = 1 Дж = 1 Н· 1 м = 105 дин · 102 см = 107 эрг. 1 кгс · м = 1 кгс · 1 м = 9, 81 Н · 1 м = 9, 81 Дж. 15
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией 1 Джоуль = 1 Дж = 1 Н· 1 м = 105 дин · 102 см = 107 эрг. 1 кгс · м = 1 кгс · 1 м = 9, 81 Н · 1 м = 9, 81 Дж. 15
 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Мощность 1 Ватт = 1 Джоуль / 1 сек. 16
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Мощность 1 Ватт = 1 Джоуль / 1 сек. 16
 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Взаимодействия между телами посредством физических полей. Физические поля – силовые поля, связанные с действием гравитационных, электрических, магнитных, ядерных сил. 17
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Взаимодействия между телами посредством физических полей. Физические поля – силовые поля, связанные с действием гравитационных, электрических, магнитных, ядерных сил. 17
 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Центральное поле - направление силы, действующей на пробную частицу в любой точке пространства, проходит через неподвижный точечный источник поля, а модуль силы зависит только от расстояния между ними. 18
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Центральное поле - направление силы, действующей на пробную частицу в любой точке пространства, проходит через неподвижный точечный источник поля, а модуль силы зависит только от расстояния между ними. 18
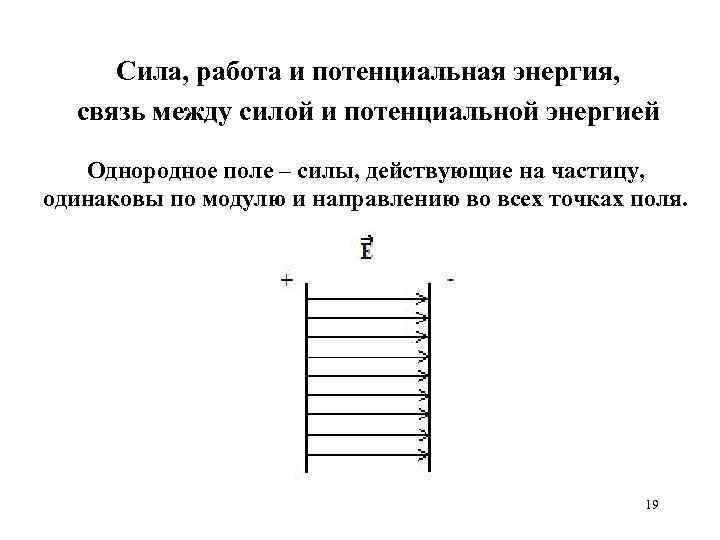 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Однородное поле – силы, действующие на частицу, одинаковы по модулю и направлению во всех точках поля. 19
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Однородное поле – силы, действующие на частицу, одинаковы по модулю и направлению во всех точках поля. 19
 Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Стационарное поле – поле, остающееся постоянным во времени. Нестационарное поле – поле, изменяющееся во времени. 20
Сила, работа и потенциальная энергия, связь между силой и потенциальной энергией Стационарное поле – поле, остающееся постоянным во времени. Нестационарное поле – поле, изменяющееся во времени. 20
 Консервативные и неконсервативные силы Консервативные силы – силы поля, работа которых над частицей в условиях стационарного поля зависит лишь от начального и конечного положений частицы и не зависит от пути, по которому двигалась частица. 21
Консервативные и неконсервативные силы Консервативные силы – силы поля, работа которых над частицей в условиях стационарного поля зависит лишь от начального и конечного положений частицы и не зависит от пути, по которому двигалась частица. 21
 Консервативные и неконсервативные силы A = (A 12)a+(A 21)b = (A 12)a – (A 12)b Работа консервативных сил не зависит от пути по определению, поэтому работа консервативных сил на замкнутом пути равна нулю. 22
Консервативные и неконсервативные силы A = (A 12)a+(A 21)b = (A 12)a – (A 12)b Работа консервативных сил не зависит от пути по определению, поэтому работа консервативных сил на замкнутом пути равна нулю. 22
 Консервативные и неконсервативные силы Поле силы тяжести Сила тяжести – везде одинаковый модуль и направление вниз по вертикали. 1 2 не зависит от пути. Сила тяжести – консервативная сила. 23
Консервативные и неконсервативные силы Поле силы тяжести Сила тяжести – везде одинаковый модуль и направление вниз по вертикали. 1 2 не зависит от пути. Сила тяжести – консервативная сила. 23
 Консервативные и неконсервативные силы Стационарное однородное поле По аналогии с полем силы тяжести всякое стационарное однородное поле – поле консервативных сил. 24
Консервативные и неконсервативные силы Стационарное однородное поле По аналогии с полем силы тяжести всякое стационарное однородное поле – поле консервативных сил. 24
 Консервативные и неконсервативные силы Центральное поле - не зависит от траектории. Центральные силы консервативны. 25
Консервативные и неконсервативные силы Центральное поле - не зависит от траектории. Центральные силы консервативны. 25
 Консервативные и неконсервативные силы Силы трения Сила трения и скорость частицы имеют противоположные направления. Работа сил трения отрицательна на любом замкнутом пути. Силы трения не консервативны. 26
Консервативные и неконсервативные силы Силы трения Сила трения и скорость частицы имеют противоположные направления. Работа сил трения отрицательна на любом замкнутом пути. Силы трения не консервативны. 26
 Работа и потенциальная энергия во внешнем поле сил Работа сил поля не зависит от пути, а зависит лишь от начального и конечного положений частицы (поле консервативных сил) - возможность сопоставить каждой точке поля некоторую функцию U(x, y, z), такую, что разность значений этой функции в точках 1 и 2 будет определять работу сил поля при переходе частицы из первой точки во вторую: 27
Работа и потенциальная энергия во внешнем поле сил Работа сил поля не зависит от пути, а зависит лишь от начального и конечного положений частицы (поле консервативных сил) - возможность сопоставить каждой точке поля некоторую функцию U(x, y, z), такую, что разность значений этой функции в точках 1 и 2 будет определять работу сил поля при переходе частицы из первой точки во вторую: 27
 Работа и потенциальная энергия во внешнем поле сил Пусть U(P) – значение функции в точке Р. АРО – работа по перемещению частицы силами поля из произвольно выбранной точки Р с функцией U(P) в точку О с функцией UО. Однозначность в определении значения имеющей размерность работы или энергии функции U(P) (работа не зависит от пути). 28
Работа и потенциальная энергия во внешнем поле сил Пусть U(P) – значение функции в точке Р. АРО – работа по перемещению частицы силами поля из произвольно выбранной точки Р с функцией U(P) в точку О с функцией UО. Однозначность в определении значения имеющей размерность работы или энергии функции U(P) (работа не зависит от пути). 28
 Работа и потенциальная энергия во внешнем поле сил А 1 О + АО 2 – работа, совершаемая силами поля при перемещении частицы из точки 1 в точку 2 по траектории, проходящей через точку О. Независимость работы А 12 = А 1 О + АО 2 от траектории перемещения из 1 в 2 (даже не через точку О). Заключение: справедливость уравнения 29
Работа и потенциальная энергия во внешнем поле сил А 1 О + АО 2 – работа, совершаемая силами поля при перемещении частицы из точки 1 в точку 2 по траектории, проходящей через точку О. Независимость работы А 12 = А 1 О + АО 2 от траектории перемещения из 1 в 2 (даже не через точку О). Заключение: справедливость уравнения 29
 Работа и потенциальная энергия во внешнем поле сил Возможность определения работы, совершаемой консервативными силами на любом пути из точки 1 в точку 2, с помощью функции U. Функция U(x, y, z) – потенциальная энергия частицы в точке с координатами (x, y, z) во внешнем поле сил. - работа, совершаемая над частицей консервативными силами, равна убыли потенциальной энергии частицы. Совершение работы за счет убыли потенциальной энергии. 30
Работа и потенциальная энергия во внешнем поле сил Возможность определения работы, совершаемой консервативными силами на любом пути из точки 1 в точку 2, с помощью функции U. Функция U(x, y, z) – потенциальная энергия частицы в точке с координатами (x, y, z) во внешнем поле сил. - работа, совершаемая над частицей консервативными силами, равна убыли потенциальной энергии частицы. Совершение работы за счет убыли потенциальной энергии. 30
 Работа и кинетическая энергия Уравнение движения частицы 31
Работа и кинетическая энергия Уравнение движения частицы 31
 Работа и кинетическая энергия Замкнутая система: - const. – кинетическая энергия частицы. 32
Работа и кинетическая энергия Замкнутая система: - const. – кинетическая энергия частицы. 32
 Работа и кинетическая энергия Т const. Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы 33
Работа и кинетическая энергия Т const. Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы 33
 Закон сохранения полной механической энергии в поле потенциальных сил Полная механическая энергия частицы находящейся в поле консервативных сил, остается постоянной. 34
Закон сохранения полной механической энергии в поле потенциальных сил Полная механическая энергия частицы находящейся в поле консервативных сил, остается постоянной. 34
 Закон сохранения полной механической энергии в поле потенциальных сил Полная механическая энергия системы невзаимодействующих частиц, на которые действуют только консервативные силы, остается постоянной. 35
Закон сохранения полной механической энергии в поле потенциальных сил Полная механическая энергия системы невзаимодействующих частиц, на которые действуют только консервативные силы, остается постоянной. 35
 Контрольный вопрос В изолированной системе сохраняется: а) кинетическая энергия, б) потенциальная энергия, в) сумма кинетической и потенциальной энергий, г) как кинетическая, так и потенциальная энергии. 36
Контрольный вопрос В изолированной системе сохраняется: а) кинетическая энергия, б) потенциальная энергия, в) сумма кинетической и потенциальной энергий, г) как кинетическая, так и потенциальная энергии. 36


