Лекция 3 05 10 2010 1

Лекция 3 (05. 10. 2010) • • 1. Динамические масс-спектрометры 2. Методы вращательной (микроволновой) и колебательной спектроскопии Следующие методы исследования, основным назначением которых является определение геометрии и электронной структуры молекул, частиц и т. п. , относятся к спектроскопическим – электронная, колебательная и вращательная спектроскопия

Динамические масс-спектрометры: 1. Времяпролетный; 2. Квадрупольный; 3. Ион-циклотронного резонанса • 1. Времяпролетный масс-спектрометр: TOF (time of flight) • L – участок дрейфа, t – время пролета ионом участка L, это время между импульсом в ИИ (импульсная электронная пушка, доли мкс) и включением Д (обычно в схеме используется осциллограф, на экране которого получается масс-спектр: зависимость величины ионного тока: ордината - от времени t: абсцисса - развертка) • М 2/2=e. V; = 2 e. V/М; t=L/ =L (М/2 e. V); М/е=2 Vt 2 • Особенности TOF-метода: компактность, быстрота проведения анализа – 10 -3 с, большой диапазон М, но малая R =М/ М 2000 – ограниченна быстродействием осциллографа. • Применение: экспресс-анализы, геохимия.

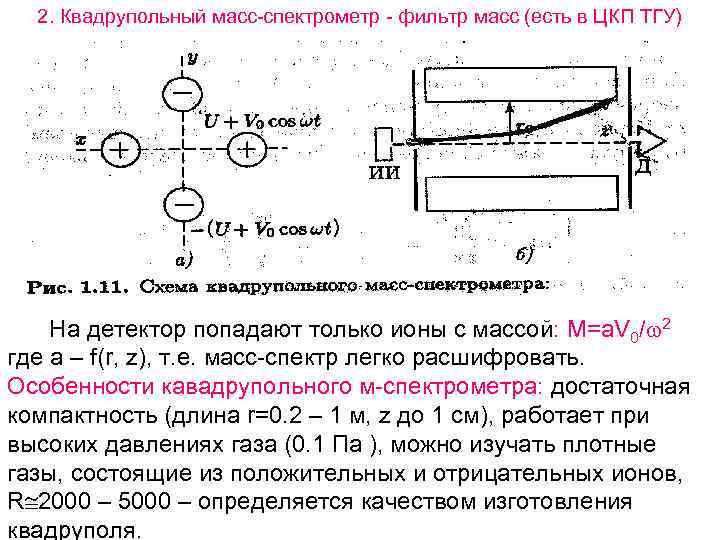2. Квадрупольный масс-спектрометр - фильтр масс (есть в ЦКП ТГУ) На детектор попадают только ионы с массой: М=a. V 0/ 2 где а – f(r, z), т. е. масс-спектр легко расшифровать. Особенности кавадрупольного м-спектрометра: достаточная компактность (длина r=0. 2 – 1 м, z до 1 см), работает при высоких давлениях газа (0. 1 Па ), можно изучать плотные газы, состоящие из положительных и отрицательных ионов, R 2000 – 5000 – определяется качеством изготовления квадруполя.

3. Спектрометр ион-циклотронного резонанса (1958) T=2 r/ , r =М /e B, T=2 (М /e B)/ =2 М/e. B, T не зависит от скорости, т. е. энергии иона. Ионы вылетают из ИИ расходящимся пучком, поэтому траекторией полета является цилиндрическая спираль, время прохождения 1 оборота одинаково для разных радиусов. Циклотронная частота вращения: c =2 /Т=e. B/М При c= - резонанс, ионный сигнал в детекторе возрастает скачком для ионов с массой М=(e B)/ с , т. е. возникает зависимость ионного тока от = e. B/М – получается масс-спектр. Особенности метода: высокие рабочие давления, используется для изучения реакций ионов с нейтральными частицами, т. к. условие резонанса не зависит от энергии (не меняется при столкновениях).

ХРОМАТОМАСС-СПЕКТРОМЕТРЫ. • В последнее время МС совмещают с хроматографами –для упрощения расшифровки мспектра: вначале разделяют сложные составы элементов на колонке, затем каждую порцию количественно исследуют на масс-спектрометре. • Т. о. , методы МС позволяют решать не только первую из поставленных задач – определение элементного состава и бруттоформулу, но и получать дополнительную информацию о структуре: • 1. Наличие осколочных, перегруппировочных ионов и т. д. указывает на соотношение энергий различных связей в молекуле. • 2. Есть информация о потенциалах ионизации, временах жизни метастабильных ионов, механизмах химических реакций и т. п.

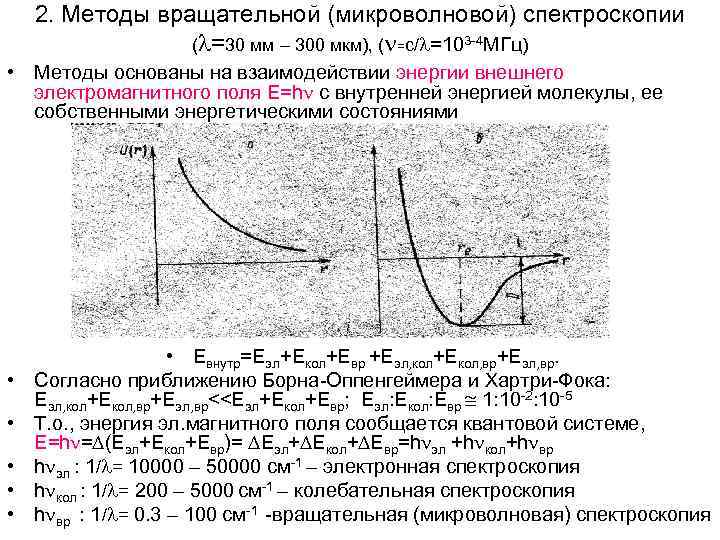2. Методы вращательной (микроволновой) спектроскопии ( =30 мм – 300 мкм), ( =с/ =103 -4 МГц) • Методы основаны на взаимодействии энергии внешнего электромагнитного поля Е=h с внутренней энергией молекулы, ее собственными энергетическими состояниями • • Евнутр=Еэл+Екол+Евр +Еэл, кол+Екол, вр+Еэл, вр. Согласно приближению Борна-Оппенгеймера и Хартри-Фока: Еэл, кол+Екол, вр+Еэл, вр<<Еэл+Екол+Евр; Еэл: Екол: Евр 1: 10 -2: 10 -5 Т. о. , энергия эл. магнитного поля сообщается квантовой системе, Е=h = (Еэл+Екол+Евр)= Еэл+ Екол+ Евр=h эл +h кол+h вр h эл : 1/ = 10000 – 50000 см-1 – электронная спектроскопия h кол : 1/ = 200 – 5000 см-1 – колебательная спектроскопия h вр : 1/ = 0. 3 – 100 см-1 -вращательная (микроволновая) спектроскопия

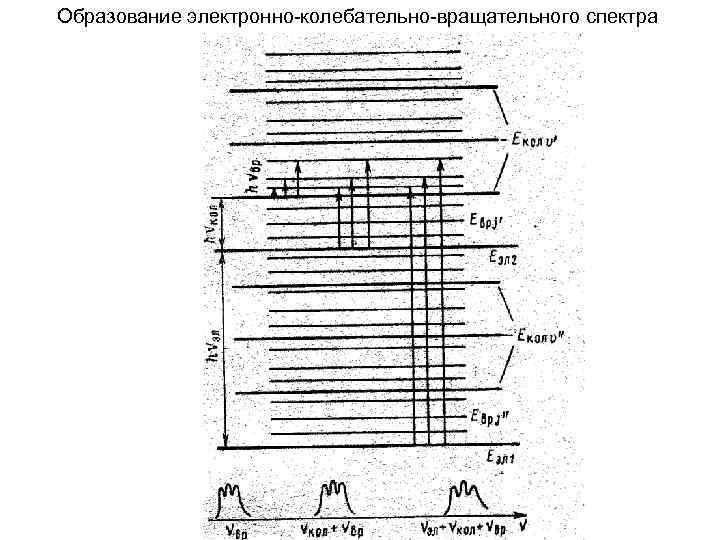Образование электронно-колебательно-вращательного спектра

Вращательные спектры двухатомных молекул (модель жесткого ротатора) • • Еэл=0; Екол=0; Евр 0; Евр=Екин=m 1 21 /2+ m 2 22 /2= m 1 r 21 2/2+ m 2 r 22 2/2= 2/2(m 1 r 12+ m 2 r 22)= =IM( 2/2)=J 2/2 IM; Евр =J 2/2 IM поскольку: линейная скорость: 1=r 1 , 2=r 2 , где - угловая скорость; момент инерции: IM = miri 2 =Mre 2; J=IM - момент количества вращательного движения равновесное расстояние: re= ri приведенная масса: M=m 1 m 2/(m 1 +m 2); J=IM -момент количества движения, который квантуется: J 2=(h 2/4 2 ) j(j+1), где j=0, 1, 2. . . , - вращательное квантовое число; тогда квантуется и энергия: • Евр= [h 2/IM 8 2] j(j+1);

Образование энергетического спектра вращающихся молекул • Евр= [h 2/IM 8 2] j(j+1); j=0, 1, 2. . . ; j= 1; • Ввр= h/(IM 8 2 ) ; Евржест=h =h. Ввр j(j+1); • Еврнежест= [h 2/(IM 8 2)] j(j+1)+С 2 j 2(j+1)2 ; С<

Образование вращательного спектра • • j= 1; вр = ( Евр)/h= Ввр[(j+2)(j+1)-j(j+1)]= 2 Ввр(j+1), т. е. расстояние между линиями в спектре =2 Ввр получив вращательный спектр, можно определить Ввр = h/IM 8 2 j: 0, 1, 2, 3, 4, j+1: 1, 2, 3, 4, 5, 6 В квантовой механике интенсивность перехода пропорциональна населенности и квадрату матричного элемента дипольного момента, т. е интенсивность отлична от 0 только для молекул с 0 (для симметричнных молекул =0, т. е. вращательный спектр отсутствует) • Населенность определяется распределением Максвела-Больцмана: существует наивероятное заселение некоторых вращательных уровней, зависящее от температуры.

Вращательные спектры многоатомных молекул 1. Сферический ротатор: Ib=Ic= Ia 2. Симметричный ротатор: Ib=Ic Ia Евр= [h 2/I 1 8 2] j(j+1)+[h 2 k 2/8 2 ] (1/I 1 -1/I 2); k –первое квантовое число –квантуется проекция момента количества движения k =0, 1, 2, . . . , j – второе – квантуется сам момент, j= k, k+1, k+2, …; j=+1; k=0. Для разных k находятся Евр , и Вврi= h/IMi 8 2 ; (R-ветвь: j=+1; Р-ветвь: j=-1); определяются I 1 и I 2 3. Асимметричный ротатор: Ib Ic Ia по 3 ветви для разных К j=+1: R ветвь j=-1: Р ветвь j=0: Q ветвь но интерпретируются вращательные спектры до сих пор проблематично, только с большими приближениями, структуры моделируются двухатомными молекулами.

Методика эксперимента во вращательной спектроскопии • 1 – клистрон, 3 – волновод, 5 – поглощающая ячейка (L=3 – 5 м, латунь), 6 – Штарковский электрод (Е 0=600 – 3000 В, 100 к. Гц; используется для модуляции линий в спектре, для калибровки радиоспектрометра используется соединение OCS с известным дипольным моментом ( 0=2. 3888 10 -30 К м): 7 – система ввода образца (0. 1 - 10 Па); 9 -детектор. • Особенности метода: • Повышение давления повышает чувствительность, но ухудшает разрешение полосы уширяются за счет столкновений; малое давление тоже плохо, т. к. без столкновений увеличивается населенность верхних уровней, т. е. наступает насыщение поглощения – чувствительность падает), для увеличения чувствительности используется Штарковский электрод: усиливаются только линии, промодулированные частотой (100 к. Гц) этого электрода. Можно определять дипольные моменты ( ) с использованием эффекта Штарка: ( )j=0 = (8 02 Е 02)/(15 h 2 0). Нельзя получать вращательные спектры бездипольных молекул • •

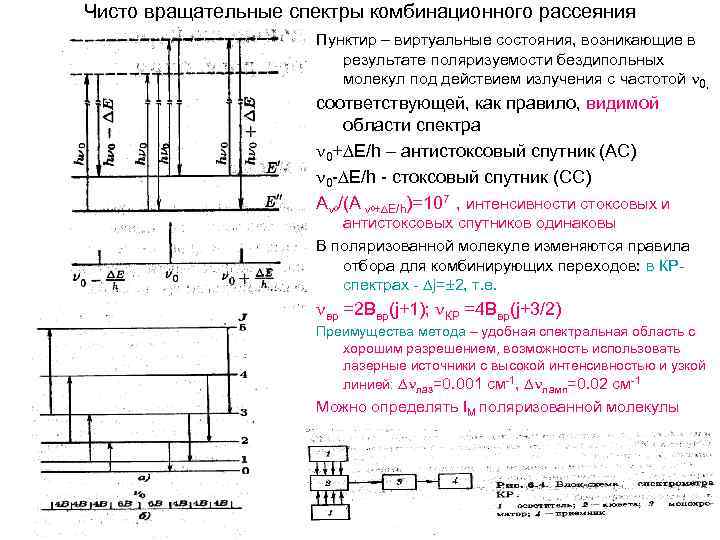Чисто вращательные спектры комбинационного рассеяния Пунктир – виртуальные состояния, возникающие в результате поляризуемости бездипольных молекул под действием излучения с частотой 0, соответствующей, как правило, видимой области спектра 0+ Е/h – антистоксовый спутник (АС) 0 - Е/h - стоксовый спутник (СС) А /(А + Е/h)=107 , интенсивности стоксовых и 0 0 антистоксовых спутников одинаковы В поляризованной молекуле изменяются правила отбора для комбинирующих переходов: в КРспектрах - j= 2, т. е. вр =2 Ввр(j+1); КР =4 Ввр(j+3/2) Преимущества метода – удобная спектральная область с хорошим разрешением, возможность использовать лазерные источники с высокой интенсивностью и узкой линией: лаз=0. 001 см-1, ламп=0. 02 см-1 Можно определять IM поляризованной молекулы

I. Колебания двухатомных молекул 1. Гармонический осциллятор 2. Ангармонический осциллятор 3. Колебательно-вращательные спектры

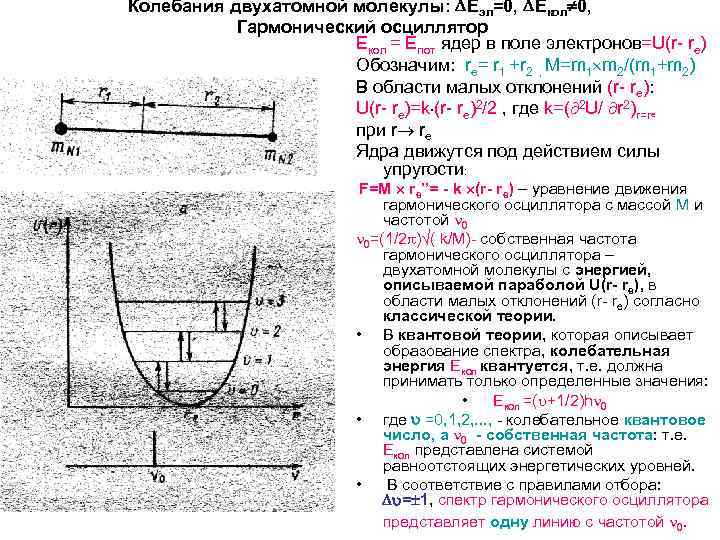Колебания двухатомной молекулы: Еэл=0, Екол 0, Гармонический осциллятор Екол = Eпот ядер в поле электронов=U(r- re) Обозначим: re= r 1 +r 2 , M=m 1 m 2/(m 1+m 2) В области малых отклонений (r- re): U(r- re)=k (r- re)2/2 , где k=( 2 U/ r 2)r=re при r re Ядра движутся под действием силы упругости: F=М re”= - k (r- re) – уравнение движения гармонического осциллятора с массой М и частотой 0 0=(1/2 ) ( k/M)- собственная частота гармонического осциллятора – двухатомной молекулы с энергией, описываемой параболой U(r- re), в области малых отклонений (r- re) согласно классической теории. • В квантовой теории, которая описывает образование спектра, колебательная энергия Екол квантуется, т. е. должна принимать только определенные значения: • Екол =( +1/2)h 0 • где =0, 1, 2, . . . , - колебательное квантовое число, а 0 - собственная частота: т. е. Екол представлена системой равноотстоящих энергетических уровней. • В соответствие с правилами отбора: = 1, спектр гармонического осциллятора представляет одну линию с частотой 0.

Ангармонический осциллятор U(r-re)=D[1 -e-a(r-re)]2 – потенциал Морзе: а=const – характеризует форму кривой; D- энергия диссоциации; а)при r , U(r-re) D б)при r re : U(r-re) D[1 -1+а(r-re)+. . . ]2 U(r-re) Da 2(r-re)2 уравнение гармонического осциллятора: k=2 Da 2 • 0=(a 2 D/M)/2 , более тяжелые атомы в молекуле и связи с малой D дают низкочастотные колебания. Екол = ( +1/2)h 0 - (h 2 02) ( +1/2)2/4 D =0, 1, 2. . . - колебательное квантовое число; =1, 2, 3. . . *= 0(1 -2 Х) фундаментальная *1=2 0(1 -3 Х) 1 ый обертон *2=3 0(1 -4 Х) 2 ой обертон D D/h; сплошной спектр; Х=h 0 /4 D Определяемые из спектров параметры молекул: D, М а, U(r-re), т. е. форма потенциальной кривой и re

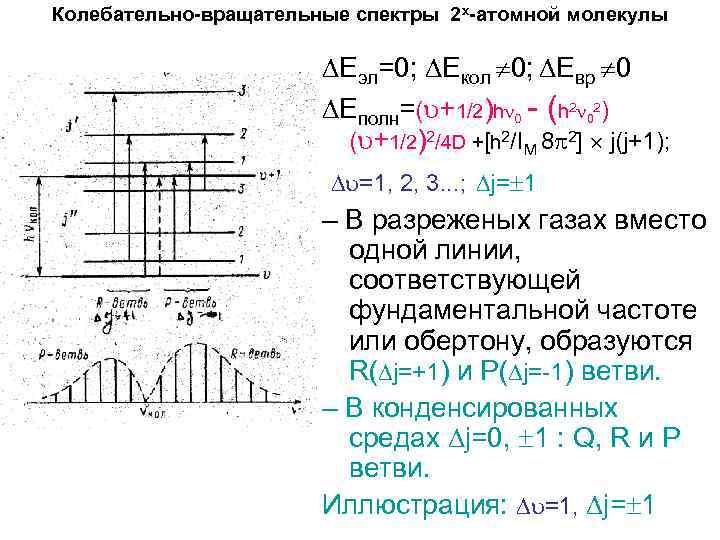Колебательно-вращательные спектры 2 х-атомной молекулы Еэл=0; Екол 0; Евр 0 Еполн=( +1/2)h 0 - (h 2 02) ( +1/2)2/4 D +[h 2/IM 8 2] j(j+1); =1, 2, 3. . . ; j= 1 – В разреженых газах вместо одной линии, соответствующей фундаментальной частоте или обертону, образуются R( j=+1) и P( j=-1) ветви. – В конденсированных средах j=0, 1 : Q, R и P ветви. Иллюстрация: =1, j= 1