25 лекция этн.pptx
- Количество слайдов: 27
 Лекция 25. Электрлік фильтрлер Фильтрлер теориясының негізгі теңдеулері және олардың анализі Төменгі жиіліктегі фильтрлер Кернеу кедергісінің ТЖФ-ға әсері
Лекция 25. Электрлік фильтрлер Фильтрлер теориясының негізгі теңдеулері және олардың анализі Төменгі жиіліктегі фильтрлер Кернеу кедергісінің ТЖФ-ға әсері
 Электрлік фильтрлер Электрлік фильтерлің жіктелуі әртүрлі қасиеттерге байланысты жүргізіледі 1. 1. Өткізу жолақтарының орналасуы бойынша жіктелуі: а) w = 0 (тұрақты ток) басталып шектік ωгр жиілігіне дейін таралатын фильтрлер төменгі жиіліктегі фильтрлер деп аталады (ТЖФ); . Основы теории цепей. Часть 2. Лекция 25 2
Электрлік фильтрлер Электрлік фильтерлің жіктелуі әртүрлі қасиеттерге байланысты жүргізіледі 1. 1. Өткізу жолақтарының орналасуы бойынша жіктелуі: а) w = 0 (тұрақты ток) басталып шектік ωгр жиілігіне дейін таралатын фильтрлер төменгі жиіліктегі фильтрлер деп аталады (ТЖФ); . Основы теории цепей. Часть 2. Лекция 25 2
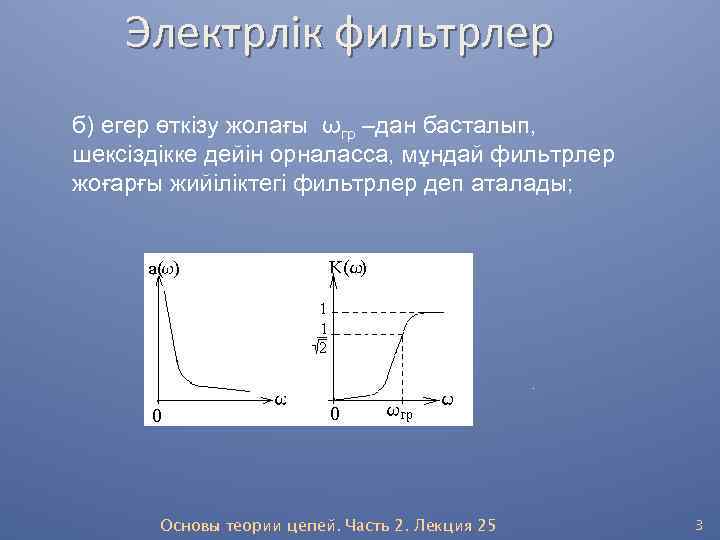 Электрлік фильтрлер б) егер өткізу жолағы ωгр –дан басталып, шексіздікке дейін орналасса, мұндай фильтрлер жоғарғы жийіліктегі фильтрлер деп аталады; . Основы теории цепей. Часть 2. Лекция 25 3
Электрлік фильтрлер б) егер өткізу жолағы ωгр –дан басталып, шексіздікке дейін орналасса, мұндай фильтрлер жоғарғы жийіліктегі фильтрлер деп аталады; . Основы теории цепей. Часть 2. Лекция 25 3
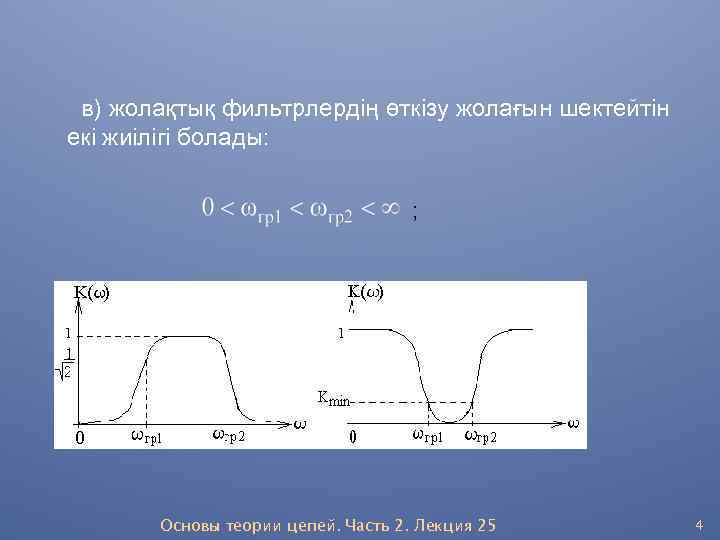 в) жолақтық фильтрлердің өткізу жолағын шектейтін екі жиілігі болады: ; Основы теории цепей. Часть 2. Лекция 25 4
в) жолақтық фильтрлердің өткізу жолағын шектейтін екі жиілігі болады: ; Основы теории цепей. Часть 2. Лекция 25 4
 г) шектеуші немесе режекторлы фильтрдің (ШФ, РФ) өткізу жолағының орнында берілген минималды деңгейінде анықталатын , шекаралық жиіліктері бар режекция фильтрі болады. Основы теории цепей. Часть 2. Лекция 25 5
г) шектеуші немесе режекторлы фильтрдің (ШФ, РФ) өткізу жолағының орнында берілген минималды деңгейінде анықталатын , шекаралық жиіліктері бар режекция фильтрі болады. Основы теории цепей. Часть 2. Лекция 25 5
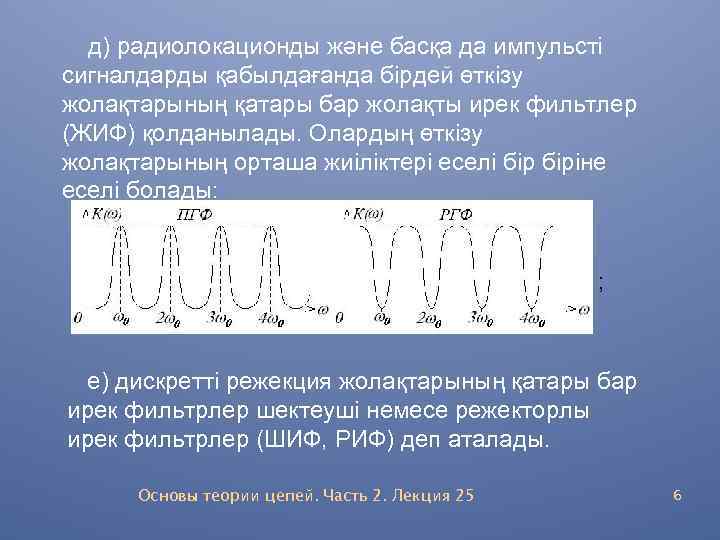 д) радиолокационды және басқа да импульсті сигналдарды қабылдағанда бірдей өткізу жолақтарының қатары бар жолақты ирек фильтлер (ЖИФ) қолданылады. Олардың өткізу жолақтарының орташа жиіліктері еселі біріне еселі болады: ; е) дискретті режекция жолақтарының қатары бар ирек фильтрлер шектеуші немесе режекторлы ирек фильтрлер (ШИФ, РИФ) деп аталады. Основы теории цепей. Часть 2. Лекция 25 6
д) радиолокационды және басқа да импульсті сигналдарды қабылдағанда бірдей өткізу жолақтарының қатары бар жолақты ирек фильтлер (ЖИФ) қолданылады. Олардың өткізу жолақтарының орташа жиіліктері еселі біріне еселі болады: ; е) дискретті режекция жолақтарының қатары бар ирек фильтрлер шектеуші немесе режекторлы ирек фильтрлер (ШИФ, РИФ) деп аталады. Основы теории цепей. Часть 2. Лекция 25 6
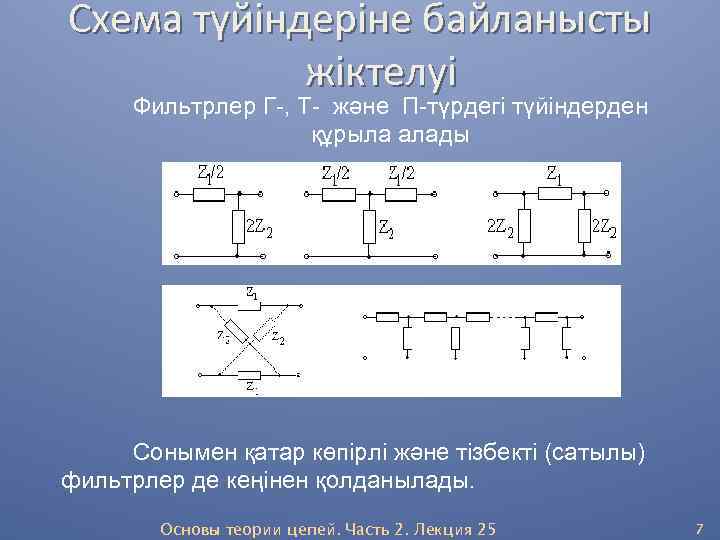 Схема түйіндеріне байланысты жіктелуі Фильтрлер Г-, Т- және П-түрдегі түйіндерден құрыла алады Сонымен қатар көпірлі және тізбекті (сатылы) фильтрлер де кеңінен қолданылады. Основы теории цепей. Часть 2. Лекция 25 7
Схема түйіндеріне байланысты жіктелуі Фильтрлер Г-, Т- және П-түрдегі түйіндерден құрыла алады Сонымен қатар көпірлі және тізбекті (сатылы) фильтрлер де кеңінен қолданылады. Основы теории цепей. Часть 2. Лекция 25 7
 3. Фильтрлердің сипаттамалық типтеріне байланысты жіктелуі: а) k типті фильтрлер (қарапайым Г-, Т- және П-түрдегі); б) m типті фильтрлер (жоғарғы ретті туынды фильтрлер); в) типті фильтрлер ; г) максималды біркелкі сипаттамалары бар фильтрлер (Баттерворт фильтрлері); д) оптималды фильтрлер (Чебышев фильтрлері). Основы теории цепей. Часть 2. Лекция 25 8
3. Фильтрлердің сипаттамалық типтеріне байланысты жіктелуі: а) k типті фильтрлер (қарапайым Г-, Т- және П-түрдегі); б) m типті фильтрлер (жоғарғы ретті туынды фильтрлер); в) типті фильтрлер ; г) максималды біркелкі сипаттамалары бар фильтрлер (Баттерворт фильтрлері); д) оптималды фильтрлер (Чебышев фильтрлері). Основы теории цепей. Часть 2. Лекция 25 8
 4. Қолданылатын элементтердің типтері бойынша жіктелуі а) реактивті (LC-фильтрлері); б) индукциясыз (RC-фильтрлері); в) активті RC-фильтрлері; г) үлестірілген параметрлері бар төртполюстіктерден жасалған фильтрлер; д) электромеханикалық фильтрлер. Основы теории цепей. Часть 2. Лекция 25 9
4. Қолданылатын элементтердің типтері бойынша жіктелуі а) реактивті (LC-фильтрлері); б) индукциясыз (RC-фильтрлері); в) активті RC-фильтрлері; г) үлестірілген параметрлері бар төртполюстіктерден жасалған фильтрлер; д) электромеханикалық фильтрлер. Основы теории цепей. Часть 2. Лекция 25 9
 Фильтрлер теориясының негізгі теңдеулері және олардың анализі Реактивті фильтрдің өткізу шарты Төртполюстіктердің сипаттамалық параметрлеріне негізделген фильтрлер теориясында келесі маңызды мәселелер шешіледі: 1) Фильтрде мөлдірлік жолақ пайда болатын шарттар орнатылады; 2) мөлдірлік жолақтың ені анықталады; 3) жиіліктік сипаттамалық теңдеулер табылады(ЖАС және ЖФС). Основы теории цепей. Часть 2. Лекция 25 10
Фильтрлер теориясының негізгі теңдеулері және олардың анализі Реактивті фильтрдің өткізу шарты Төртполюстіктердің сипаттамалық параметрлеріне негізделген фильтрлер теориясында келесі маңызды мәселелер шешіледі: 1) Фильтрде мөлдірлік жолақ пайда болатын шарттар орнатылады; 2) мөлдірлік жолақтың ені анықталады; 3) жиіліктік сипаттамалық теңдеулер табылады(ЖАС және ЖФС). Основы теории цепей. Часть 2. Лекция 25 10
 Фильтрлер теориясының негізгі теңдеулері және олардың анализі Г-түрдегі түптұлға түйін үшін тікелей беріліс параметріндегі теңдеулер жүйесі ақиқат: Основы теории цепей. Часть 2. Лекция 25 11
Фильтрлер теориясының негізгі теңдеулері және олардың анализі Г-түрдегі түптұлға түйін үшін тікелей беріліс параметріндегі теңдеулер жүйесі ақиқат: Основы теории цепей. Часть 2. Лекция 25 11
 Фильтрлер теориясының негізгі теңдеулері және олардың анализі Төртполюстіктердің теориясында көрсетілуі бойынша, Г-түрдегі түптұлға түйін үшін сипаттамалық кедергілер (екіжақты келісім режиміндегі кіріс кедергілері) төмендегідей анықталады: . Беріліс тұрақтысы (беріліс өлшемі) қатынастан анықталады келесі . Основы теории цепей. Часть 2. Лекция 25 12
Фильтрлер теориясының негізгі теңдеулері және олардың анализі Төртполюстіктердің теориясында көрсетілуі бойынша, Г-түрдегі түптұлға түйін үшін сипаттамалық кедергілер (екіжақты келісім режиміндегі кіріс кедергілері) төмендегідей анықталады: . Беріліс тұрақтысы (беріліс өлшемі) қатынастан анықталады келесі . Основы теории цепей. Часть 2. Лекция 25 12
 Т- және П-түрдегі симметриялы схемалар үшін Фильтр сипаттамалық кедергіге тең кедергіге жүктеліп тұрғандықтан, кіріс және шығыс кернеулері мен токтарының қатынасы: . Основы теории цепей. Часть 2. Лекция 25 13
Т- және П-түрдегі симметриялы схемалар үшін Фильтр сипаттамалық кедергіге тең кедергіге жүктеліп тұрғандықтан, кіріс және шығыс кернеулері мен токтарының қатынасы: . Основы теории цепей. Часть 2. Лекция 25 13
 Т- және П-түрдегі симметриялы схемалар үшін Мөлдірлік жолағының анықтамасынан, а = 0 өшуі жалған өлшем екендігі шығады , cos b [– 1; + 1] интервалында өзгере алады, сондықтан: . Основы теории цепей. Часть 2. Лекция 25 14
Т- және П-түрдегі симметриялы схемалар үшін Мөлдірлік жолағының анықтамасынан, а = 0 өшуі жалған өлшем екендігі шығады , cos b [– 1; + 1] интервалында өзгере алады, сондықтан: . Основы теории цепей. Часть 2. Лекция 25 14
 Т- және П-түрдегі симметриялы схемалар үшін Сонымен өткізу жолағы орын алуы үшін және әртүрлі таңбалы, ал абсолютті мәні бойынша келесі шарт орындалуы қажетті және жеткілікті: : | | < 4 | |. Основы теории цепей. Часть 2. Лекция 25 15
Т- және П-түрдегі симметриялы схемалар үшін Сонымен өткізу жолағы орын алуы үшін және әртүрлі таңбалы, ал абсолютті мәні бойынша келесі шарт орындалуы қажетті және жеткілікті: : | | < 4 | |. Основы теории цепей. Часть 2. Лекция 25 15
 Фильтрлер теориясының негізгі теңсіздігін қолданып, өткізу жолағының шекаралық жиіліктерін бірнеше тәсілмен анықтауға болады: . 1. Егер берілетін функция түрі және болса, онда шекаралық жиіліктер келесі теңдеулер жүйесін шешкенде табылады Основы теории цепей. Часть 2. Лекция 25 16
Фильтрлер теориясының негізгі теңсіздігін қолданып, өткізу жолағының шекаралық жиіліктерін бірнеше тәсілмен анықтауға болады: . 1. Егер берілетін функция түрі және болса, онда шекаралық жиіліктер келесі теңдеулер жүйесін шешкенде табылады Основы теории цепей. Часть 2. Лекция 25 16
 2. Егер жиіліктік тәуелділіктер және графикалық түрде берілсе, онда өткізу жолағының шекаралық жиіліктері де графикалық түрде анықтала алады Основы теории цепей. Часть 2. Лекция 25 17
2. Егер жиіліктік тәуелділіктер және графикалық түрде берілсе, онда өткізу жолағының шекаралық жиіліктері де графикалық түрде анықтала алады Основы теории цепей. Часть 2. Лекция 25 17
 3. Шекаралық жиіліктерді сипаттамалық кедергілерді қарастыру арқылы табуға болады . және әртүрлі таңбасында және көбейтіндісі нақты сан, сондықтан өткізу жолағындағы сипаттамалық кедергілер де нақты сан болады Основы теории цепей. Часть 2. Лекция 25 18
3. Шекаралық жиіліктерді сипаттамалық кедергілерді қарастыру арқылы табуға болады . және әртүрлі таңбасында және көбейтіндісі нақты сан, сондықтан өткізу жолағындағы сипаттамалық кедергілер де нақты сан болады Основы теории цепей. Часть 2. Лекция 25 18
 4. Шекаралық жиіліктер бос жүріс кезіндегі беріліс коэффициенті бірге тең жиілік ретінде анықтала алады. Бұл анықтама фильтрлерді эксперименталды зерттеген кезде өте тиімді. Келесі тәуелділіктер фильрдің жиіліктік сипаттамалары болып табылады : а(w) –жиіліктік-амплитудалық сипаттама; b(w) –жиіліктік-фазалық сипаттама. Основы теории цепей. Часть 2. Лекция 25 19
4. Шекаралық жиіліктер бос жүріс кезіндегі беріліс коэффициенті бірге тең жиілік ретінде анықтала алады. Бұл анықтама фильтрлерді эксперименталды зерттеген кезде өте тиімді. Келесі тәуелділіктер фильрдің жиіліктік сипаттамалары болып табылады : а(w) –жиіліктік-амплитудалық сипаттама; b(w) –жиіліктік-фазалық сипаттама. Основы теории цепей. Часть 2. Лекция 25 19
 Нақты және жорамал бөліктерді бөліп, келесі теңдіктерді аламыз Өткізу жолағында а = 0, сондықтан, Основы теории цепей. Часть 2. Лекция 25 20
Нақты және жорамал бөліктерді бөліп, келесі теңдіктерді аламыз Өткізу жолағында а = 0, сондықтан, Основы теории цепей. Часть 2. Лекция 25 20
 Жиіліктік-амплитудалық сипаттама а(w) = 0 өткізу жолағында жиілік осіне бірлеседі. Басылу жолағында сондықтан: . Басылу жолағында жиіліктік-фазалық сипаттама: b(w) = ± p. Основы теории цепей. Часть 2. Лекция 25 21
Жиіліктік-амплитудалық сипаттама а(w) = 0 өткізу жолағында жиілік осіне бірлеседі. Басылу жолағында сондықтан: . Басылу жолағында жиіліктік-фазалық сипаттама: b(w) = ± p. Основы теории цепей. Часть 2. Лекция 25 21
 Төменгі жиілікті фильтрлер Өткізу жолағындағы а(w) жиіліктік-амплитудалық және b(w) жиіліктік-фазалық сипаттамалар келесі формулалармен анықталады Основы теории цепей. Часть 2. Лекция 25 22
Төменгі жиілікті фильтрлер Өткізу жолағындағы а(w) жиіліктік-амплитудалық және b(w) жиіліктік-фазалық сипаттамалар келесі формулалармен анықталады Основы теории цепей. Часть 2. Лекция 25 22
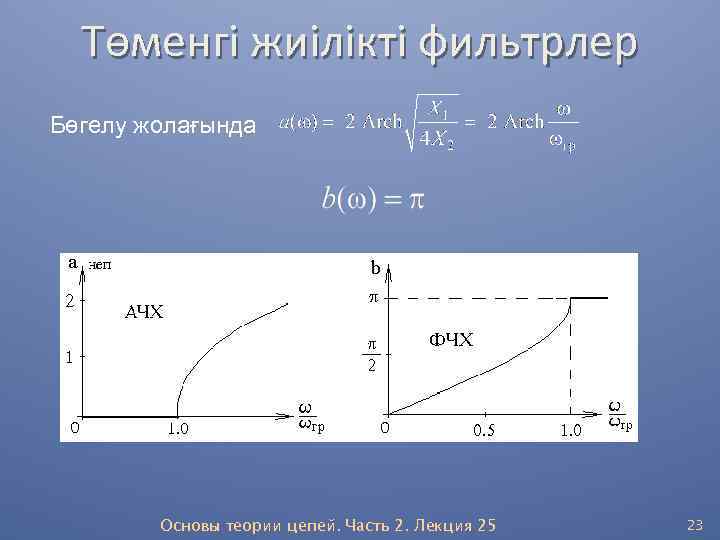 Төменгі жиілікті фильтрлер Бөгелу жолағында . Основы теории цепей. Часть 2. Лекция 25 23
Төменгі жиілікті фильтрлер Бөгелу жолағында . Основы теории цепей. Часть 2. Лекция 25 23
 Фильтр сипаттамалық кедергіге тең кедергіге жүктелген жағдайда ғана жиіліктік сипаттамалар келесі түрде болады: Жиіліктік-фазалық сипаттаманың оң екендігін дәлелдеу үшін векторлық диаграммаларды қарастырайық. Мысалы, келісімді кедергіге жүктелген Т-түрдегі төменгі жиілікті фильтр Основы теории цепей. Часть 2. Лекция 25 24
Фильтр сипаттамалық кедергіге тең кедергіге жүктелген жағдайда ғана жиіліктік сипаттамалар келесі түрде болады: Жиіліктік-фазалық сипаттаманың оң екендігін дәлелдеу үшін векторлық диаграммаларды қарастырайық. Мысалы, келісімді кедергіге жүктелген Т-түрдегі төменгі жиілікті фильтр Основы теории цепей. Часть 2. Лекция 25 24
 Основы теории цепей. Часть 2. Лекция 25 25
Основы теории цепей. Часть 2. Лекция 25 25
 Кернеу кедергісінің ТЖФ-ге әсері Бұл схеманың беріліс функциясы: . Берілу коэффициентінің модулі: . Основы теории цепей. Часть 2. Лекция 25 26
Кернеу кедергісінің ТЖФ-ге әсері Бұл схеманың беріліс функциясы: . Берілу коэффициентінің модулі: . Основы теории цепей. Часть 2. Лекция 25 26
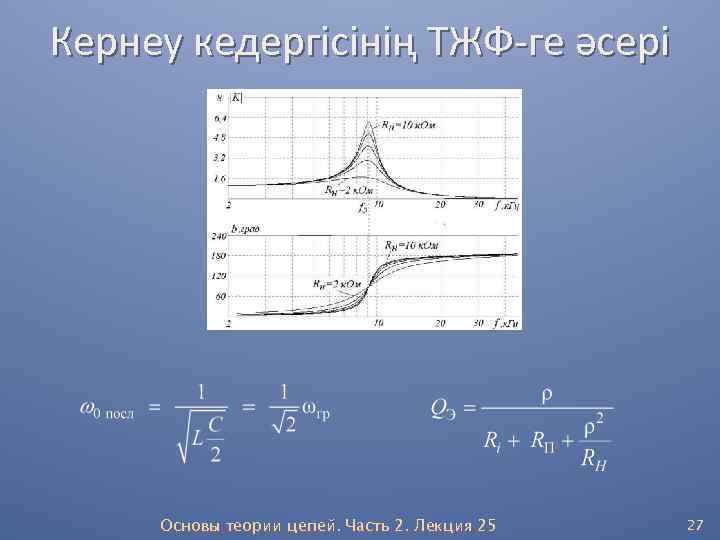 Кернеу кедергісінің ТЖФ-ге әсері Основы теории цепей. Часть 2. Лекция 25 27
Кернеу кедергісінің ТЖФ-ге әсері Основы теории цепей. Часть 2. Лекция 25 27


