Лекция 22 1 2 План лекции Определение расхода

Лекция 22 1. 2. План лекции Определение расхода энергии на движение поезда аналитическим способом. Графический способ построения кривой расхода энергии. 1. Определение расхода энергии на движение поезда аналитическим способом Расход энергии на движение поезда весом G тонн на перегоне длиной LП с заданным профилем пути i. Э может быть найден аналитическим методом. Найдем прежде всего выражение для определения работы, совершенной тяговыми двигателями на участке движения под током Aдв. Эта работа совершается очевидно за время движения с включенными двигателями и равна сумме работ, затрачиваемых на преодоление сопротивлений движению поезда и на накопление кинетической энергии поезда. Эта работа может быть выражена следующим образом: (22. 1)

где l. I – путь пройденный от начала перегона до пункта, в котором выключаются тяговые двигатели, т. е. за время хода поезда под током, км; Vв – скорость в момент выключения тяговых двигателей, км/ч; коэффициент 9, 81/3600 = 2, 725 · 10 -3 служит для перевода килограммометров в ватт-часы. После отключения ТЭД за время выбега скорость поезда снижается с величины Vв, в момент начала выбега, до скорости начала торможения VT, в момент начала торможения. Благодаря чему за счет расходования накопленной кинетической энергии поезда преодолевается сила сопротивления движению на пути выбега – lв. Уравнение энергетического баланса за время выбега записывается: (22. 2) Выражая из (22. 2) и подставляя его значение в (22. 1), получим: (22. 3) 2

Учитывая, что l. I + lв = LП – l. T, где l. Т – путь торможения, км, можно придать (22. 3) следующий вид: (22. 4) Первый член этой формулы представляет, очевидно, энергию, затраченную на преодоление сопротивлений движению поезда на всем перегоне LП, а второй и третий члены – потери в тормозах при остановке поезда. Как видно из формулы, потери в тормозах равны кинетической энергии поезда в момент начала торможения за вычетом работы сил сопротивления движению на тормозном пути l. Т, так как эта работа уже учтена в первом члене выражения (22. 4). Чтобы упростить полученную формулу введем в нее эквивалентный уклон i. Э. Эквивалентным по расходу энергии уклоном i. Э (измеряемый в тысячных долях, ‰) называется такой неизменный на всем участке уклон, при котором работа, расходуемая на преодоление суммарного сопротивления движению и на потери в тормозах на спусках, равна этой же работе на действительном профиле линии. 3

4 Кроме того, заменим в формуле переменное удельное основное сопротивление движению средним по всему перегону сопротивлением движению wcp, а удельное основное сопротивление движению на тормозном пути – его средним значением, которое обозначим через w. T. Это позволит вынести сопротивления движению за знак интеграла и тем самым заменить интеграл произведениями средних значений сопротивления движению на пройденный путь. Среднее основное сопротивление движению может быть определено по кривым w'O(V) при движении без тока при скорости, на 5 -10% превышающий среднюю ходовую скорость. Сопротивление движению w. T может быть приближенно взято по этой же кривой w'O(V) при скорости V = 0, 7·VT. Принимая движение во время торможения равномерно замедленным с некоторым средним тормозным замедлением a. T, м/с2, тормозной путь l. T будет равен: (22. 5)

Учитывая также, что приведенная масса поезда m равна: (22. 6) выражение (22. 4) может быть представлено следующим образом: (22. 7) В последнем члене (22. 7), выражающем работу сил сопротивления движению на тормозном пути, вместо эквивалентного подъема i. Э введен средний уклон i. T на пути торможения, поскольку этот уклон может быть не равен эквивалентному. Чтобы определить энергию, подведенную к тяговым двигателям необходимо выражение (22. 7) разделить на средний КПД двигателя и передачи ср. 5

Подобный способ учета потерь в ТЭД и передаче вполне допустим, так как в пределах рабочей части характеристик двигателя КПД изменяется не значительно. Среднее значение КПД ср может быть взято на 1 – 1, 5% ниже его максимального значения по характеристике (I). При переменном токе в величине ср должны быть учтены потери в трансформаторе и преобразователе. В этом случае: (22. 8) Для того чтобы получить общий расход энергии на движение поезда следует учесть ещё потери в пусковых устройствах. Эти потери, как известно, равны полезной работе, совершенной двигателями за период пуска, умноженной на коэффициент пусковых потерь KП, который зависит от способа пуска. 6

Полезная работа двигателей за период пуска равна: (22. 9) где l. П – путь пройденный поездом за период пуска, км. Следовательно, потери энергии в пусковых устройствах АП равны: (22. 10) Заменяя, как и ранее, переменное основное сопротивление движению и действительные уклоны соответственно средними их значениями w. П и i. П на пусковом участке пути l. П, а также выражая массу поезда через его вес и принимая движение за время пуска равномерно ускоренным с ускорением a. П, м/с2, получим: (22. 11) 7

Прибавив пусковые потери, выражаемые формулой (22. 11) к выражению (22. 8), получим общий расход энергии А, затрачиваемой на движение поезда весом G тонн на перегоне длиной LП километров: (22. 12) Разделив обе части полученной формулы (22. 12) на вес поезда G и длину перегона LП, получим следующее выражение для определения удельного расхода энергии на движение поезда: (22. 13) 8

Пути пуска l. П и торможения l. Т невелики по сравнению с общей длиной перегона LП, особенно в условиях электрической тяги, поэтому для упрощения расчетов по (22. 12) и (22. 13) в большинстве случаев вполне допустимо принимать вместо уклонов i. П и i. Т эквивалентный уклон (i. П = i. T = i. Э) или же вообще пренебречь ими i. П = i. T = 0. Допустимо также заменить сопротивление движению w. П и w. T средним значением основного удельного сопротивления движению w. СР. Для городской электрической тяги можно вообще отказаться от учета вторых членов в квадратных скобках и пользоваться упрощенной формулой: (22. 14) В случае применения рекуперативного торможения значительно сокращаются потери, связанные с торможениями поезда. Если эти потери равнялись AT при механическом или реостатном торможении, то для покрытия их, из сети необходимо было забрать энергию АТ/ СР. При рекуперации во время торможения возвращается энергия в сеть, равная АТ· РЕК (где РЕК – средний КПД рекуперации) и, следовательно, общее потребление энергии на торможение сокращается до: 9

(22. 15) Поэтому в случае применения рекуперативного торможения следует умножать член формулы (22. 13), выражающий потери в тормозах на величину (1 - СР· РЕК). Если рекуперативное торможение производится не до полной остановки поезда, а лишь до некоторой минимальной скорости VK, то на коэффициент (1 - СР· РЕК) следует умножать лишь ту часть потерь в тормозах, которая соответствует снижению скорости от VT до VK. Поэтому в расчетные формулы необходимо подставлять вместо квадрата скорости начала торможения VT 2 величину: (22. 16) Для полного учета энергии, потребляемой поездом, необходимо добавить к расходу энергии на движение поезда расход на его собственные нужды. Если средняя мощность расходуемая на все собственные нужды равна РСН ватт, то удельный расход энергии (АУД)СН на собственные нужды можно выразить формулой: (22. 17) где VЭ – эксплуатационная скорость, км/ч. 10

11 Удельный расход энергии на собственные нужды тем ниже, чем выше средняя эксплуатационная скорость поезда. Общий удельный расход энергии, отнесенный к первичной стороне тяговых подстанций (АУД)ТП определяется по формуле: (22. 18) В отличие от расчета расхода энергии по кривым движения, расчеты по формуле (22. 18) дают представление не только об общем расходе энергии, но и о влиянии на него отдельных слагающих. Работа, затрачиваемая на преодоление основного сопротивления движению, выражается членом 2, 725·w. CP; дополнительная работа, зависящая от трасы и профиля, т. е. работа, затрачиваемая на преодоление кривых, изменение потенциальной энергии поезда и потери в тормозах на спусках – членом 2, 725·i. Э.

12 Потери в тормозах при остановках поезда представлены членами формул, пропорциональными VT 2. Потери в двигателях и передачах (а также трансформаторах и преобразователях) учитываются делением суммы перечисленных слагаемых на средний КПД СР. Потери в пусковых устройствах выражаются членами формулы, пропорциональными VП 2. Расход энергии на собственные нужды учитывается либо поправочным коэффициентом КСН, либо же отдельным членом формулы расхода энергии. Наконец, потери в тяговой сети и на тяговых подстанциях учитываются делением суммы всех остальных членов, соответственно на КПД КС и ТП. 2. Графический способ построения кривой расхода энергии Расход энергии на движение поезда может быть определен графическим построение кривой расхода энергии в функции пути А(l) по кривой движения V(l) и характеристике I(V). Элементарный расход энергии А на любом элементе пути l, который поезд проходит за время t при средней скорости VC, равен: (22. 19)

13 где IC – средний ток, потребляемый поездом на элементе пути l. Этот ток IC с достаточной точностью можно находить по кривым диаграммы I(V) для скорости, соответствующей VC. Так как: (22. 20) то, подставляя это выражение в (22. 19) и разделяя переменные получим: (22. 21) Полагая, что , можно записать (22. 22) Следовательно, в геометрическом понимании равняется катету прямоугольного треугольника с другим катетом, равным l при угле , противолежащим катету.

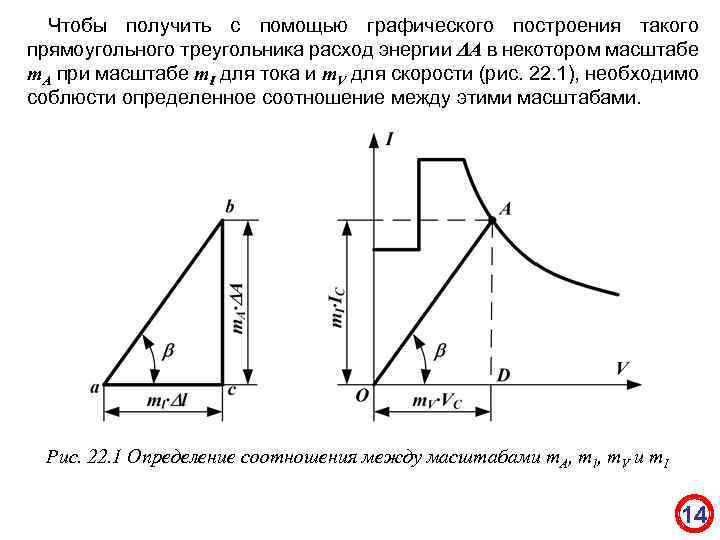Чтобы получить с помощью графического построения такого прямоугольного треугольника расход энергии А в некотором масштабе m. A при масштабе m. I для тока и m. V для скорости (рис. 22. 1), необходимо соблюсти определенное соотношение между этими масштабами. Рис. 22. 1 Определение соотношения между масштабами m. A, ml, m. V и m. I 14

15 Из треугольника abc получим: (22. 23) Но из другого треугольника OAD на рис. 21. 1, следует, что: (22. 24) поэтому (22. 25) или согласно выражения (22. 21) (22. 26) откуда (22. 27)

Таким образом, произвольно можно задаться только тремя масштабами из четырех. Обычно берут удобный масштаб m. A, масштабы m. V и ml выбираются при построении кривой V(l). Масштаб m. I, в котором вычерчивается кривая I(V), определяется в соответствии с (22. 28): (22. 28) Построение кривой расхода энергии A(l) показано на рис. 22. 2. На кривой I(V) определяем точки 1, 2, 3…, дающие средние значения токов IC 1, IC 2, IC 3… для средних скоростей движения VC 1, VC 2, VC 3… на элементах пути l 1, l 2, l 3, …. Начало координат O диаграммы I(V) соединяем лучами с точками 1, 2, 3, …, что позволяет определить углы 1, 2, 3, … Из точки O' – начала построения кривой V(l) проводим прямую O'I под углом 1 к оси абцисс до пересечения с вертикальной прямой, проведенной из конца первого элемента пути l 1. Для этого достаточно провести прямую O'I параллельно лучу O 1, если оси координат кривых V(l) и I(V) расположены, как показано на рис. 22. 2. тогда согласно доказанному выше проекция луча O'I на ось ординат в масштабе m. A будет равна расходу энергии А 1 на элементе пути l 1. 16

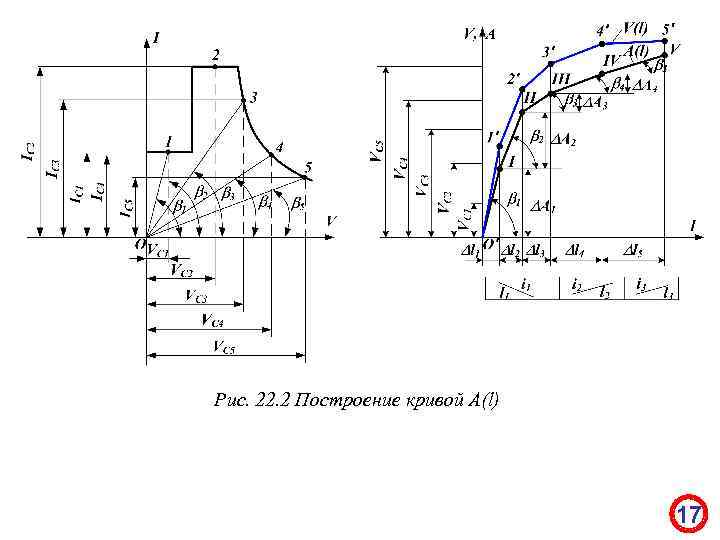Рис. 22. 2 Построение кривой A(l) 17

Далее из точки I проводим прямую I – II параллельную лучу О 2 в пределах элемента пути l 2, и получим приращение энергии А 2 в виде проекции прямой I- II на ось ординат. Из точки II проводим прямую II – III параллельную лучу O 3 в пределах элемента пути l 3 и т. д. Через точки I, III, … будет проходить искомая кривая А(l). Последняя ее ордината дает полный расход энергии на всем перегоне. В случае рекуперативного торможения ток поезда становится отрицательным, все лучи переходят в нижний координатный угол кривой I(V), а ординаты кривой А(l) начнут уменьшаться. При делении кривой I(V) на интервалы, следует стремиться, чтобы внутри каждого интервала не происходило резкого изменения тока и скорости. В частности, моменты включения и выключения тока и перехода с одной ступени соединения двигателей на другую не должны попадать внутрь интервала. Если повернуть диаграмму I(V) на 900, то отрезки кривой A(l) будут не параллельны, а перпендикулярны лучам O 1, O 2, O 3 и т. д. Такой способ построения зависимости A(l) также может быть применим на практике. 18